二分查找原理
-
二分查找java
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。 示例 1: 输入: nums = [-1,0,3,5,9,12], target = 9 输出: 4 解释: 9 出现在 nums 中并且下标为 4 示例 2: 输入: nums = [-1,0,3,5,9,12], target = 2 输出:
-
算法-二分查找、移除元素
伪装成一个老手! 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。 示例 1: 输入: nums = [-1,0,3,5,9,12], target = 9 输出: 4 解释: 9 出现在 nums 中并且下标为 4 来源:力扣二分查找 1. Q1: 为
-
【算法】简单的二分查找算法
一个简单的二分查找算法: 简单描述:算法由静态方法rank()实现,它接受一个整数键和一个有序的int数组作为参数,如果整数存在于数组,返回它的索引,否则返回-1,算法使用两个变量lo和hi,并保证整数如果存在于数组中则它一定存在于a[lo...hi]中,然后通过循
-
算法(3)——二分查找
二分查找也称折半查找,是在一组有序(升序/降序)的数据中查找一个元素,它是一种效率较高的查找方法。 1、查找的目标数据元素必须是有序的。没有顺序的数据,二分法就失去意义。 2、数据元素通常是数值型,可以比较大小。 3、将目标元素和查找范围的中间值做比较(
-
二分查找与判定树
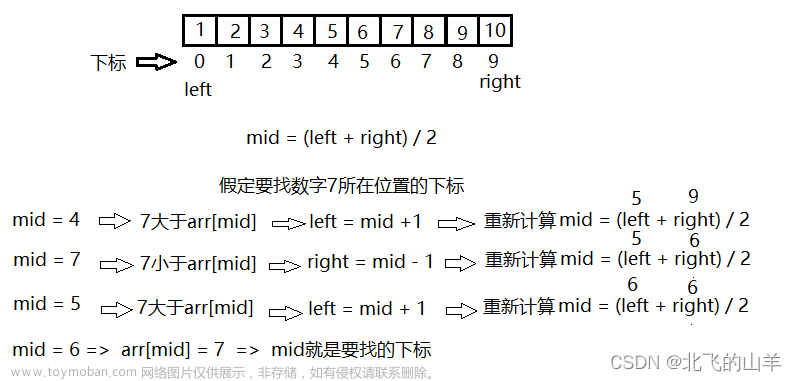
二分查找也称“折半查找”,要求查找表为采用 顺序存储结构 的 有序表。本例一律采用升序排列。 二分查找每一次都会比较给定值与序列[low,high]的中间元素,该元素的下标为mid = (low+high)/2,若两者相等,则返回元素的下标为mid;如果arr[mid]key,说明给定值key在中间元素的左边,
-
【算法】二分查找——BinarySearch
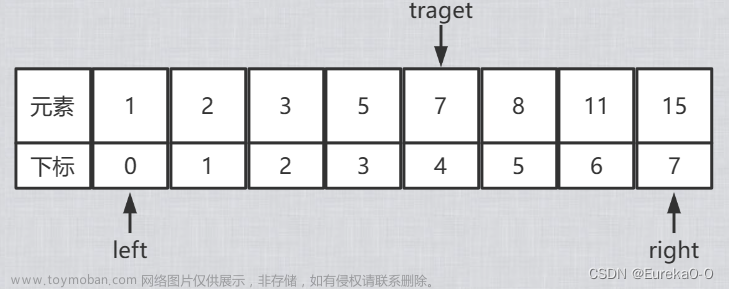
二分查找又称折半查找,是一种能够大幅减少时间复杂度的查找方法,但是二分查找要求线性表必须词用顺序储存结构,而且表中元素按有序排列。 在后续讨论中,我们假设有序表递增有序。 二分查找中使用的术语: 目标 Target —— 你要查找的值 索引 Index —— 你要
-
二分查找的讲义和视频
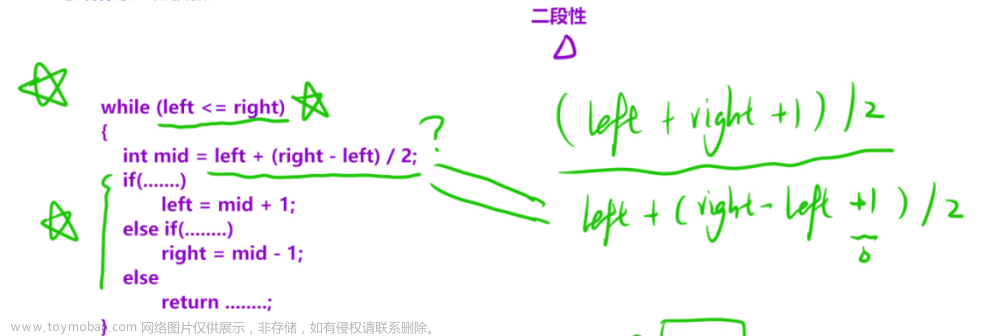
源码下载: https://pan.baidu.com/s/1wMsUK4hZpdttFzOK66n3mQ?pwd=x7a7 提取码 x7a7 先进入《 视频教程及配套源 码》,再进入《 C++ 算法》。 在线看视频: https://www.bilibili.com/video/BV1nL411Q7DY/ 1.1.1. 最简单的情况 a. 情况简述 数组已经按升序排好序。 假定要找的数一定存在。 如果存
-
【C语言】二分查找(详解)
🎥 岁月失语唯石能言的个人主页 🔥 个人栏专: 秒懂C语言 ⭐ 若在许我少年时,一两黄金一两风 目录 一、二分查找的思路 二、思路分析 2.1定义变量 2.2逻辑分析 三、代码实现 总结 二分查找是一种高效的查找算法,尤其适用于有序数组。它的基
-
学习心得:二分查找
当你需要找到目标元素的第一个和最后一个出现位置时,你可以通过稍作修改来实现。以下是一个引导你思路的步骤: 找到第一个出现位置: 使用标准的二分查找算法找到目标元素。 如果找到目标元素,检查它的前一个元素是否也是目标元素,如果是,则继续在左侧搜索,
-
二分查找(C语言实现)
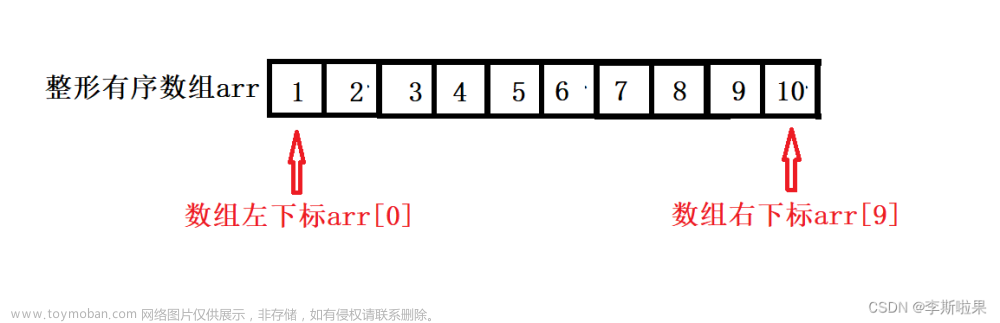
二分查找的前提: 一个整形有序数组中 查找具体某个数 以下以数组元素为偶数个做例 二分查找(折半查找)的思想:对于已按排序的序列,经过一次比较,可将序列分割成两部分,然后只在有可能包含待查元素的一部分中继续查找,并根据试探结果继续分割,逐
-
C语言之二分查找
目录 一、二分查找算法 二、分支语句中应注意的小点 所谓二分查找,就是要在一组 有序的数列 中,查找给定的数是否在此数列中。 最主要的步骤有三个: 1.确定被查找的范围的左右下标left、right 2.根据left和right,确定中间元素的下标mid 3.根据mid锁定的元素和查找的元素
-
【C语言】二分查找
在 有序表 中,每次都取 中间元素 作为比较的对象。 如果给中间值与给定值相等,则查找成功,返回该元素的下标/索引; 如果中间值大于给定值,则在中间值的右半区间继续查找; 如果中间值小于给定值,则在中间值的左半区间继续查找; 确定了该元素所在范围那么范围
-
力扣75——二分查找
总结leetcode75中的 二分查找 算法题解题思路。 上一篇:力扣75——堆/优先队列 题目: 题解: 二分查找。用 left 、 right 分别记录左端点和右端点。然后计算出它们的平均值 mid ,接着用 guess(mid) 判断是大了还是小了。 题目: 题解: 先 快速排序 ,然后用 upper_bound() 找到第一
-
「算法」二分查找1:理论&细节
🎇 个人主页 :Ice_Sugar_7 🎇 所属专栏 :算法详解 🎇 欢迎点赞收藏加关注哦! 这个算法的特点就是: 细节多,出错率高,很容易就写成死循环 有模板,但切记要 在理解的基础上记忆 ,不要死记硬背。有三个模板,一个是本文要讲的 简单模板 ,另外两个分别是 查找左、
-
java实现二分查找算法
递归实现: public static int binarySearchRecursive(int[] arr, int target) { return binarySearchRecursive(arr, target, 0, arr.length - 1); } private static int binarySearchRecursive(int[] arr, int target, int low, int high) { if (low high) { return -1; // 没有找到目标元素 } int mid = (low + high) / 2
-
每日一题 — 二分查找
704. 二分查找 - 力扣(LeetCode) 朴素二分查找模板: 代码:
-
【算法小课堂】二分查找算法
当我们要从一个序列中查找一个元素的时候,最快想到的方法就是顺序查找法(即:从前到后依次查找)。但这种方法过于无脑,就是暴力的把每个元素都排查一遍。元素个数少的时候还行,一旦元素个数多起来,效率是非常低下,所以在实际中这种查找的方法是被摒弃的。
-
二分查找图解
使用二分查找的前提是所给的元素集合必须是 单调 的。 注意:本文图文并茂 将提供以下图文链接供大家理解: 图文链接: 飞书图解链接🎉🎉🎉 密码: 2k85154 模板代码,展开查看 元素存在 返回对应元素的下标 元素不存在 返回最大小于该元素的元素的下标 模板代码,展
-
【二分查找】详细图解
目录 一.什么是二分查找法? 二.算法要求 三.算法思想 图解(要找的数k的值为3) 参考代码 二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序储存结构,而且表中元素按有序排列。 1.必须是 有序排列。
-
【算法优选】 二分查找专题——贰
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用 顺序存储结构 ,而且表中元素按 有序排列 。 查找过程 : 首先,假设表中元素是按升序排列,将表中间位置记录的与查找比较,如果两者相等,