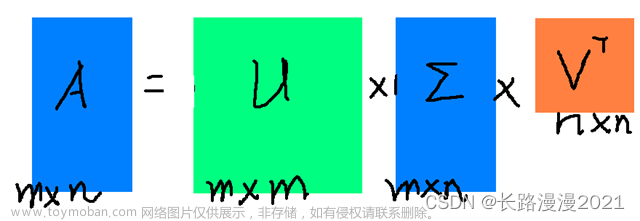
低秩分解的应用
-
Matlab实现矩阵的QR分解和奇异值分解
1.安装并运行matlab软件; 2.在命令窗口行输入需要进行QR分解的矩阵,并输入求秩及进行QR分解的函数,如下图; 3.点击回车键,则可得Q及R矩阵; 4.若要查看之前所输入的矩阵及所获得的相关变量,可从右侧工作区窗口查看; 5.单击需要查看的变量名,则相关变量会被显示在主窗口
-
时序分解 | Matlab实现NGO-VMD北方苍鹰算法优化变分模态分解时间序列信号分解
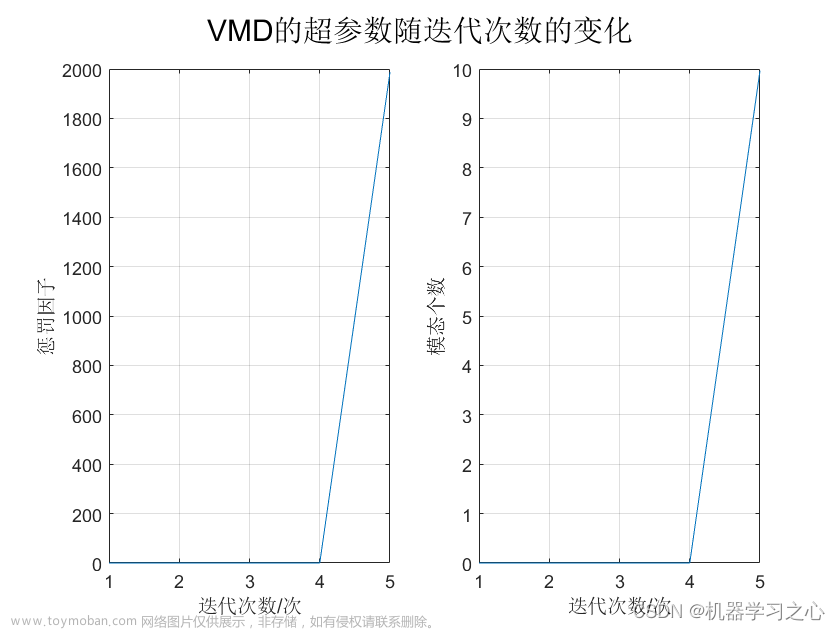
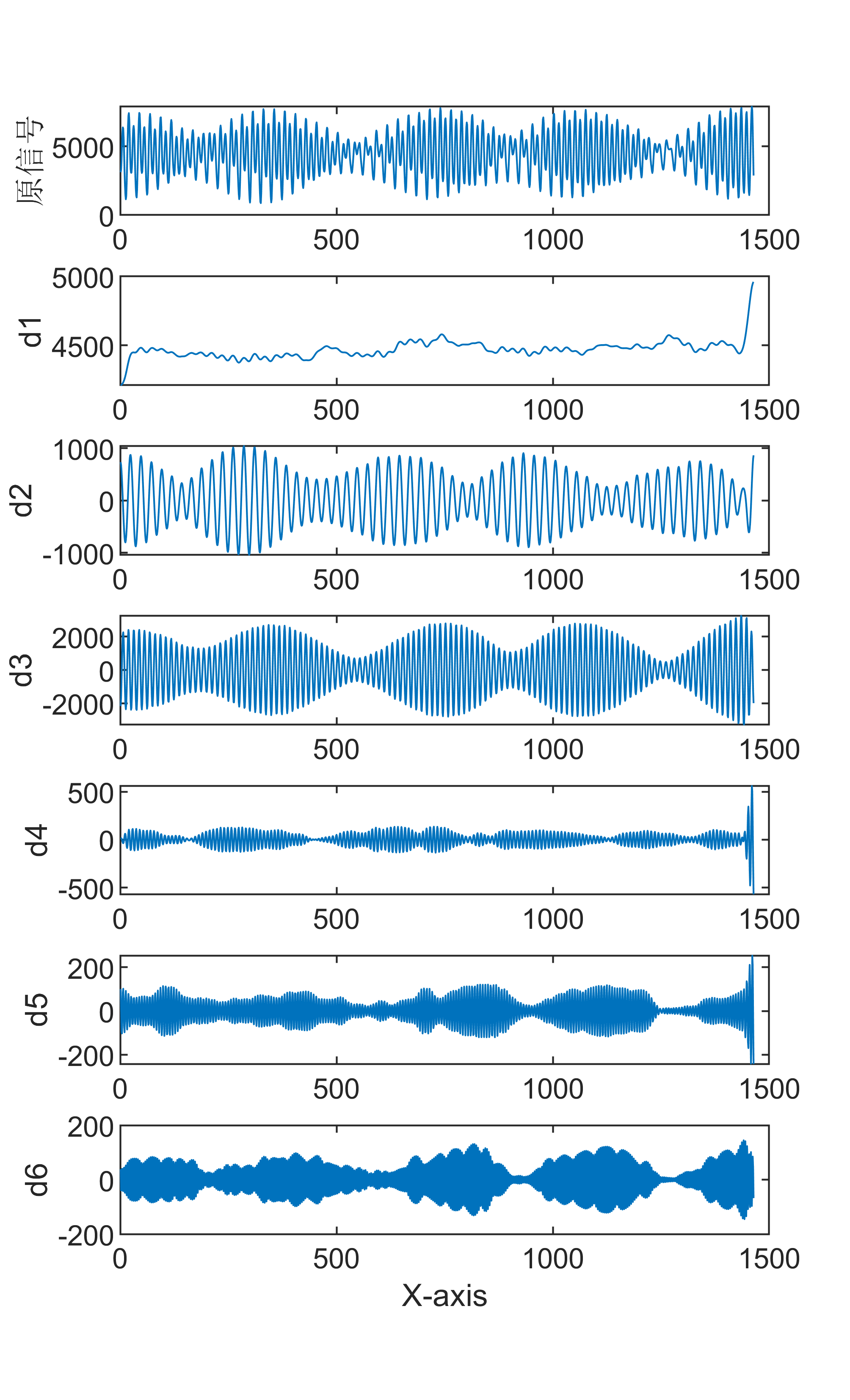
效果一览 基本介绍 北方苍鹰算法NGO优化VMD,对其分解层数,惩罚因子数做优化,利用NGO优化算法确定其最佳参数,适应度函数为样本熵。 NGO-VMD北方苍鹰算法NGO优化VMD变分模态分解 可直接运行 分解效果好 适合作为创新点(Matlab完整源码和数据) 1.利用北方苍鹰算法算法优化
-
【MATLAB】逐次变分模态分解SVMD信号分解算法
有意向获取代码,请转文末观看代码获取方式~ 逐次变分模态分解(Sequential Variational Mode Decomposition,简称SVMD)是一种用于信号处理和数据分析的方法。它可以将复杂的信号分解为一系列模态函数,每个模态函数代表了信号中的一个特定频率成分。 SVMD的主要目标是提取信号中
-
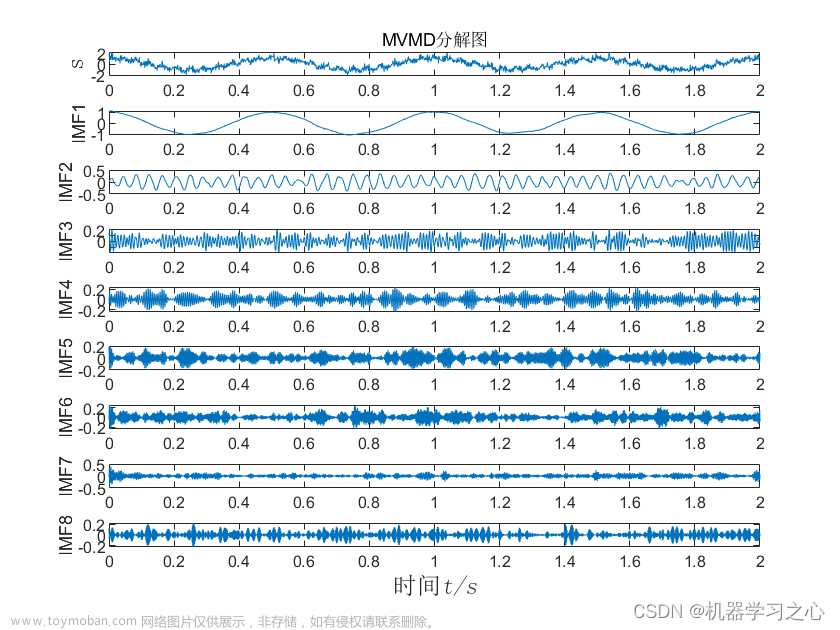
【MATLAB】 多元变分模态分解MVMD信号分解算法
有意向获取代码,请转文末观看代码获取方式~ 多元变分模态分解(MVMD)是一种信号分解方法,可以自适应地实现信号的频域剖分及各分量的有效分离。 MVMD算法的具体步骤如下: 假设原始信号S被分解为K个分量μ,保证分解序列为具有中心频率的有限带宽的模态分量,同时各
-
矩阵的谱分解 (详细推导步骤~~~特征值分解特征向量
所谓矩阵的分解,就是将一个矩阵写成结构比较简单的或性质比较熟悉的另一些矩阵的乘积。矩阵的分解方法有很多种,包括三角分解、QR(正交三角)分解、最大秩分解、奇异值分解和谱分解,所有这些分解在数值代数和最优化问题的解法中都扮演着十分重要的角
-
机器学习——奇异值分解二(特征分解+SVD纯理解,头疼系列)
特征值和特征向量的定义 抄来的:奇异值分解 困惑1:特征值和特征向量,和原矩阵是怎样的关系,需要一个栗子进行更具象的认识 困惑2:为什么多个特征向量组合成的矩阵,可以构成矩阵A的特征分解?需要推导 困惑3:为什么要特征向量标准化? 困惑4:标准正交基是什么
-
Matlab中求解线性方程组——高斯消元法、LU分解法、QR分解法、SVD分解法、迭代法等
MATLAB迭代的三种方式以及相关案例举例 MATLAB矩阵的分解函数与案例举例 MATLAB当中线性方程组、不定方程组、奇异方程组、超定方程组的介绍 MATLAB语句实现方阵性质的验证 MATLAB绘图函数的相关介绍——海底测量、二维与三维图形绘制 MATLAB求函数极限的简单介绍 文章目录 前言
-
机器学习实战:Python基于SVD奇异值分解进行矩阵分解(八)
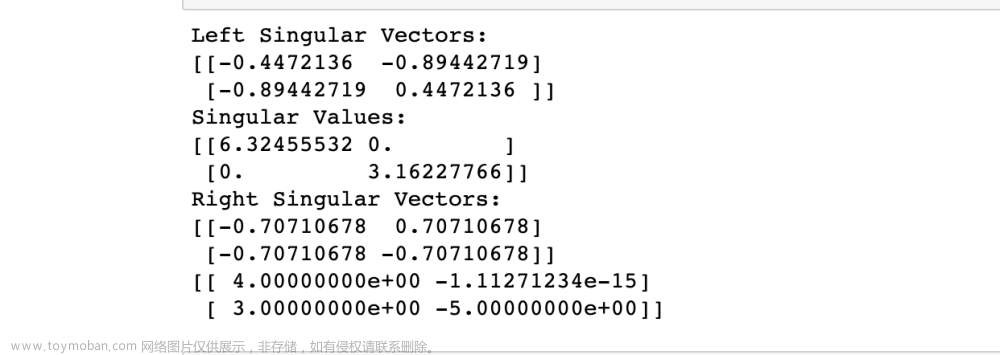
1.1 奇异值分解 奇异值分解( Singular Value Decomposition,SVD )是一种重要的矩阵分解技术,它可以将一个矩阵分解为三个矩阵的乘积,分别为左奇异矩阵、奇异值矩阵和右奇异矩阵。SVD 的原理可以描述如下: 对于任意 m × n m times n m × n 的矩阵 A A A ,它的 SVD 分解为: A = U $
-
矩阵理论| 基础:线性子空间(非平凡子空间)、空间分解、直和分解
前置:线性代数学习笔记3-5:秩1矩阵和矩阵作为“向量”构成的空间 空间 V mathbf V V 有子空间 V 1 mathbf V_1 V 1 (一组基为 α 1 , α 2 , . . . , α k alpha_1,alpha_2,...,alpha_k α 1 , α 2 , ... , α k )和子空间 V 2 mathbf V_2 V 2 (一组基为 β 1 , β 2 , . . . , β l beta_1,beta_2,
-
对称矩阵的三对角分解(Lanzos分解算法)-MINRES算法预热
这篇博客看完以后接着看下一篇博客添加链接描述专门介绍MINRES算法实现就容易了 首先介绍Lanczos分解,Lanzos把对称矩阵转换为一个三对角对称矩阵。考虑三对角对称矩阵如下,考虑正交分解 T = Q T A Q T = Q^T A Q T = Q T A Q T = ( α 1 β 1 0 ⋯ 0 0 β 1 α 2 β 2 0 ⋯ 0 0 β 2 α 3 β 3 ⋯ 0
-
矩阵篇(五)-- 特征值分解(EVD)和奇异值分解(SVD)
设 A n × n A_{n times n} A n × n 有 n n n 个线性无关的特征向量 x 1 , … , x n boldsymbol{x}_{1}, ldots, boldsymbol{x}_{n} x 1 , … , x n ,对应特征值分别为 λ 1 , … , λ n lambda_{1}, ldots, lambda_{n} λ 1 , … , λ n A [ x 1 ⋯ x n ] = [ λ 1 x 1 ⋯ λ n x n ] Aleft[begin{array}{lll
-
时序分解 | MATLAB实现MVMD多元变分模态分解信号分量可视化
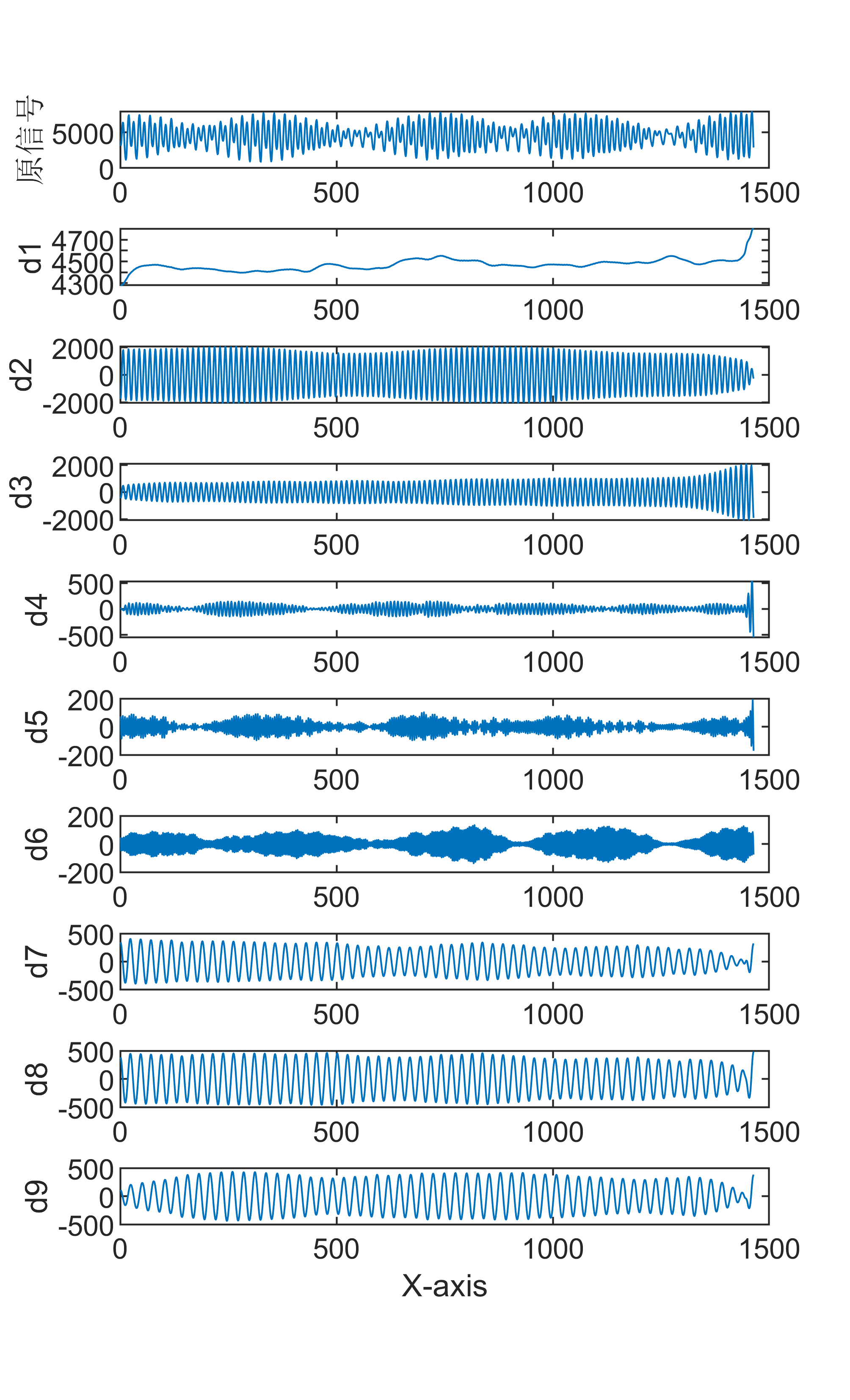
效果一览 基本介绍 MVMD多元变分模态分解 可直接替换 Matlab语言 1.算法新颖小众,用的人很少,包含分解图,效果如图所示,适合作为创❤️~ 2.直接替换数据即可用 适合新手小白 注释清晰~ 3.附赠测试数据 直接运行main一键出图~ 程序设计 完整源码和数据获取方式:私信
-
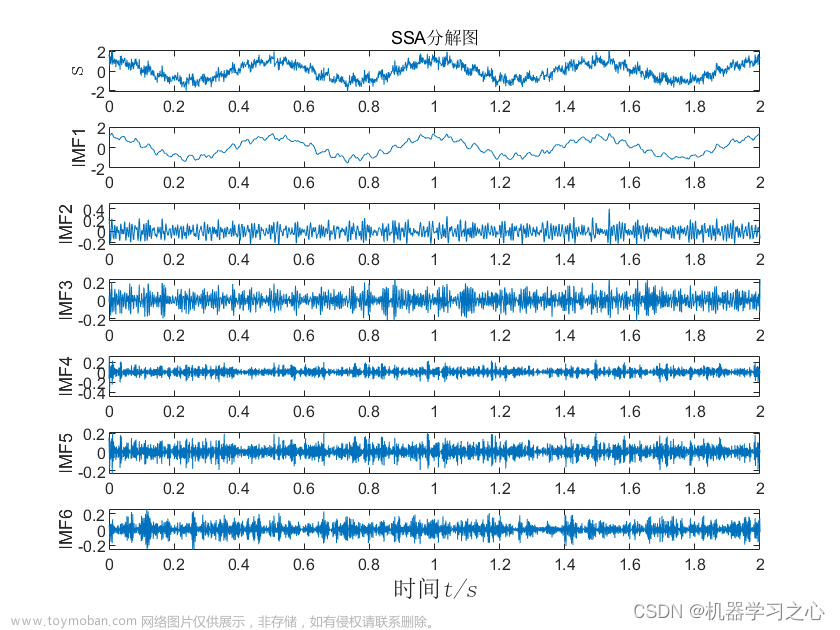
时序分解 | MATLAB实现基于SSA奇异谱分析的信号分解分量可视化
效果一览 基本介绍 奇异谱分解奇异谱分析SSA 可直接替换txt数据运行 Matlab 1.分解效果图 ,效果如图所示,可完全满足您的需求~ 2.直接替换txt数据即可用 适合新手小白 注释清晰~ 3.附赠案例数据 直接运行main一键出图~ 程序设计 完整源码和数据获取方式:MATLAB实现基于S
-
洛谷——P1069 [NOIP2009 普及组] 细胞分裂(分解质因数,唯一分解定理)
Hanks 博士是 BT(Bio-Tech,生物技术)领域的知名专家。现在,他正在为一个细胞实验做准备工作:培养细胞样本。 Hanks 博士手里现在有 N N N 种细胞,编号从 1 ∼ N 1 sim N 1 ∼ N ,一个第 i i i 种细胞经过 1 1 1 秒钟可以分裂为 S i S_i S i 个同种细胞( S i S_i S i 为正整数)。
-
一分钟读懂:矩阵的特征值分解、奇异值分解和伪逆矩阵
通过把矩阵运算分解成多个矩阵的乘法,可以简化矩阵运算,也可发现对应线性变换的一些内在规律和特性。根据不同的目的,有不同的分解策略。本文我们讨论最常用的特征值分解和奇异值分解。 定义了矩阵的加、减、乘、除(逆)运算后,数学家们自然希望探索矩阵更多
-
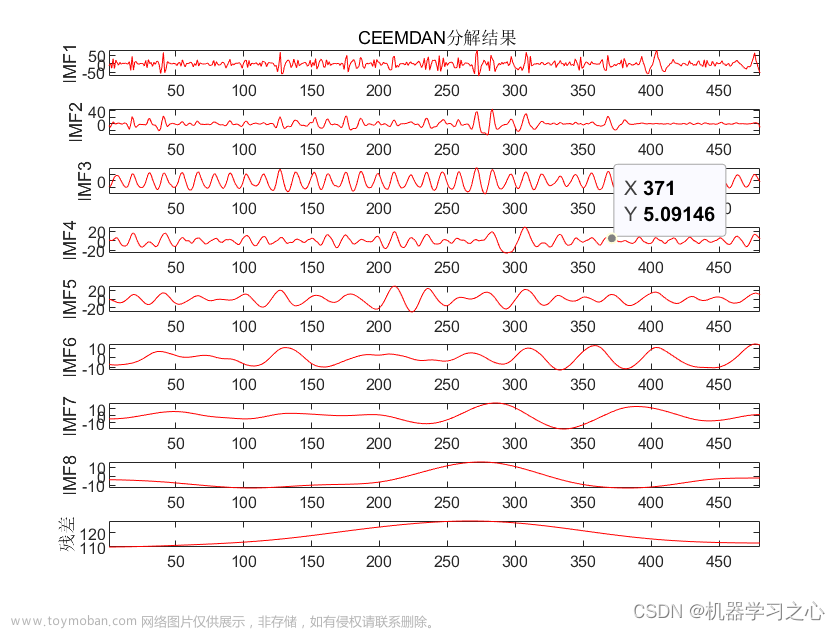
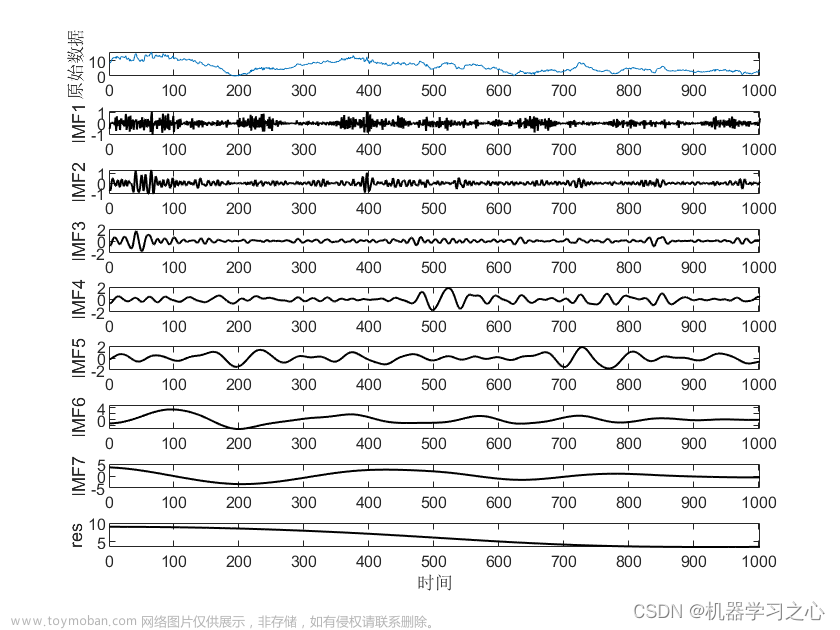
时序分解 | Matlab实现CEEMDAN+PE自适应噪声完备集合经验模态分解+排列熵计算
效果一览 基本介绍 CEEMDAN+PE自适应噪声完备集合经验模态分解+排列熵计算 运行环境matlab2018及以上(完整源码和数据) 1.CEEMDAN是改进的EMD,借用了EEMD方法中加入高斯噪声和通过多次叠加并平均以抵消噪声,效果更好,可用做信号分解、时间序列分解集成预测、故障诊断等等
-
时序分解 | MATLAB实现ICEEMDAN+SE改进的自适应经验模态分解+样本熵重构分量
效果一览 基本介绍 ICEEMDAN+SE改进的自适应经验模态分解+样本熵重构分量 包括频谱图 避免了传统经验模态分解的一些固有缺陷 效果更佳 附赠案例数据 可直接运行 直接替换excel数据即可使用 适合新手小白 程序设计 完整源码和数据获取方式:私信回复 MATLAB实现ICEEMDAN+SE改进的
-
类EMD的“信号分解方法”及MATLAB实现(第八篇)——离散小波变换DWT(小波分解)
在之前的系列文章里,我们介绍了EEMD、CEEMD、CEEMDAN、VMD、ICEEMDAN、LMD、EWT,我们继续补完该系列。 今天要讲到的是小波分解,通常也就是指离散小波变换(Discrete Wavelet Transform, DWT)。在网上有一些介绍该方法的文章,但是总感觉不够通俗或不够透彻,希望读完这篇能让你有
-
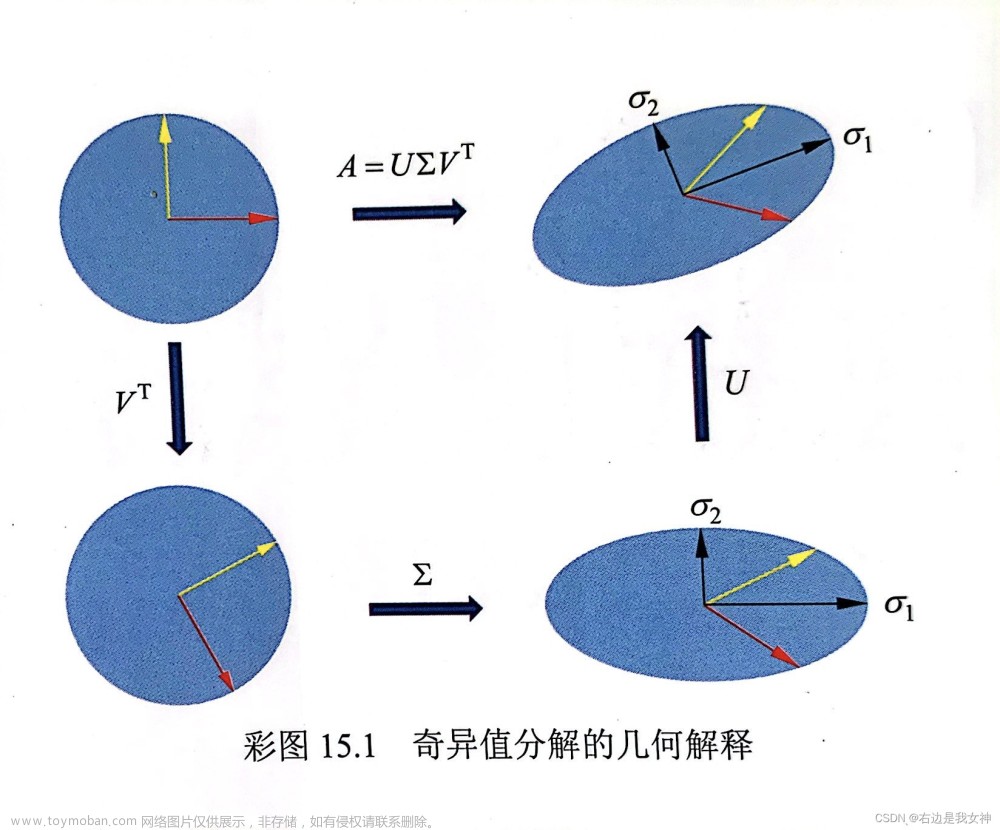
第十五章 奇异值分解
奇异值分解(SVD)是一种矩阵因子分解方法。 任意一个 m × n mtimes n m × n 矩阵,都可以表示为三个矩阵的乘积(因子分解)形式,分别是 n n n 阶正交矩阵、由降序排列的非负的对角线元素组成的 m × n mtimes n m × n 的矩形对角矩阵和 n n n 阶正交矩阵。 矩阵的奇异值分解一定
-
Mybatis分解式查询
目录 一、Mybatis一对多分解式查询 1. 新增持久层接口方法 2. 新增映射文件对应的标签 3. 新增测试方法 4. 运行效果 二、Mybatis一对