低秩矩阵分解
-
矩阵理论| 基础:线性子空间(非平凡子空间)、空间分解、直和分解
前置:线性代数学习笔记3-5:秩1矩阵和矩阵作为“向量”构成的空间 空间 V mathbf V V 有子空间 V 1 mathbf V_1 V 1 (一组基为 α 1 , α 2 , . . . , α k alpha_1,alpha_2,...,alpha_k α 1 , α 2 , ... , α k )和子空间 V 2 mathbf V_2 V 2 (一组基为 β 1 , β 2 , . . . , β l beta_1,beta_2,
-
对称矩阵的三对角分解(Lanzos分解算法)-MINRES算法预热
这篇博客看完以后接着看下一篇博客添加链接描述专门介绍MINRES算法实现就容易了 首先介绍Lanczos分解,Lanzos把对称矩阵转换为一个三对角对称矩阵。考虑三对角对称矩阵如下,考虑正交分解 T = Q T A Q T = Q^T A Q T = Q T A Q T = ( α 1 β 1 0 ⋯ 0 0 β 1 α 2 β 2 0 ⋯ 0 0 β 2 α 3 β 3 ⋯ 0
-
矩阵篇(五)-- 特征值分解(EVD)和奇异值分解(SVD)
设 A n × n A_{n times n} A n × n 有 n n n 个线性无关的特征向量 x 1 , … , x n boldsymbol{x}_{1}, ldots, boldsymbol{x}_{n} x 1 , … , x n ,对应特征值分别为 λ 1 , … , λ n lambda_{1}, ldots, lambda_{n} λ 1 , … , λ n A [ x 1 ⋯ x n ] = [ λ 1 x 1 ⋯ λ n x n ] Aleft[begin{array}{lll
-
【矩阵分析】线性空间、λ矩阵、内积空间、Hermite矩阵、矩阵分解、矩阵范数、矩阵函数
单纯矩阵 :A可对角化⇔①A可对角化;⇔②n个线性无关的特征向量; ⇔③每个特征值的几何重复度等于代数重复度;⇔④特征值λi对应的pi = n - rank(λiE - A)。 等价矩阵 :A(λ)等价于B(λ)⇔① 任意k阶行列式因子相同Dk(λ);⇔②有相同的不变因子dk(λ);⇔③相同的初等因子,且
-
运用谱分解定理反求实对称矩阵
设三阶 实对称矩阵 A A A ,若矩阵 A A A 的特征值为 λ 1 , λ 2 , λ 3 lambda_1,lambda_2,lambda_3 λ 1 , λ 2 , λ 3 ,对应的 单位化 特征向量分别为 α 1 , α 2 , α 3 alpha_1,alpha_2,alpha_3 α 1 , α 2 , α 3 且 两两正交 ,则 A = λ 1 α 1 α 1 T + λ 2 α 2 α 2 T + λ 3 α 3 α 3 T A = lam
-
第三章,矩阵,07-用初等变换求逆矩阵、矩阵的LU分解
玩转线性代数(19)初等矩阵与初等变换的相关应用的笔记,例见原文 已知: A r ∼ F A^r sim F A r ∼ F ,求可逆阵 P P P ,使 P A = F PA = F P A = F ( F F F 为 A A A 的行最简形) 方法:利用初等行变换,将矩阵A左边所乘初等矩阵相乘,从而得到可逆矩阵P. 步骤: (1)对矩阵A进行l次初等
-
【国科大——矩阵分析与应用】LU分解
LU分解是旨在将某个矩阵表示为两个或多个矩阵的乘积。 LU分解是将矩阵表示为 A A A = L L L U U U ,其中 L L L 矩阵 代表 Lower Triangular(下三角矩阵) , U U U 矩阵 代表 Upper Triangular(上三角矩阵) 。形象一点就相当于写为 A = ◣ ∗ ◥ A=◣*◥ A = ◣ ∗ ◥ 。 1. 求解U矩阵 先求U矩
-
详解矩阵的三角分解A=LU
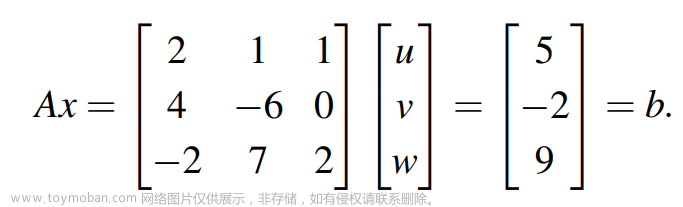
目录 一. 求解Ax=b 二. 上三角矩阵分解 三. 下三角矩阵分解 四. 矩阵的三角分解 举例1:矩阵三角分解 举例2:三角分解的限制 举例3:主元和乘法因子均为1 举例4:U为单位阵 小结 我们知道高斯消元法可以对应矩阵的基础变换。先来看我们比较熟悉的Ax=b模型,如下: 解这个方
-
高等代数复习:矩阵的满秩分解
本篇文章适合个人复习翻阅,不建议新手入门使用 定义:矩阵的左逆、右逆 设 A A A 是 m × n mtimes n m × n 矩阵 若 r ( A ) = n r(A)=n r ( A ) = n ,即 A A A 列满秩,则存在秩为 n n n 的 n × m ntimes m n × m 行满秩矩阵 B B B ,使得 B A = I n BA=I_n B A = I n ,矩阵 B B B 称为 A A A 的左逆 若
-
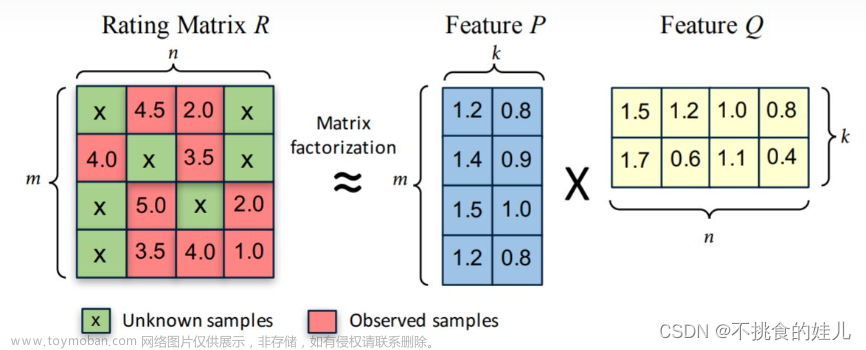
推荐算法之--矩阵分解(Matrix Factorization)
在众多推荐算法或模型的发展演化脉络中,基于 矩阵分解 的推荐算法,处在了一个关键的位置: 向前承接了 协同率波 的主要思想,一定程度上提高了处理稀疏数据的能力和模型泛化能力,缓解了头部效应; 向后可以作为 Embedding 思想的一种简单实现,可以很方便、灵活地
-
Python实现矩阵奇异值分解(SVD)
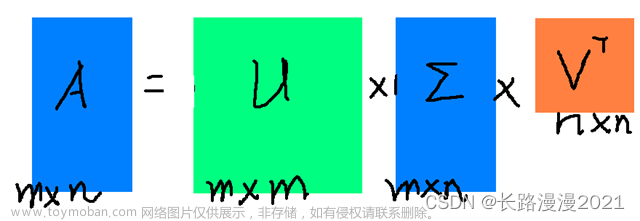
Python实现矩阵奇异值分解(SVD) 矩阵奇异值分解(Singular Value Decomposition, SVD)是一种重要的矩阵分解方法,可以将一个矩阵分解成三个矩阵的乘积,即 A = U Σ V T A=USigma V^{T} A = U Σ
-
最优化方法(三)——矩阵QR分解
1.熟练掌握 QR 分解 Gram–Schmidt方法; 2.掌握 Householder 方 法 ; 3. 能够判断 矩阵是否可逆 ,并 求出其逆矩阵 。 读取附件 MatrixA.mat 文件中的 矩阵 A , 利用 Gram–Schmidt(GS) 算法对A进行QR分解 。 (1) 验证GS是否 能稳定 进行QR分解矩阵A ,其 Q矩阵 是否正交? (2) 实现 Householder
-
半正定Toeplitz矩阵的范德蒙德分解
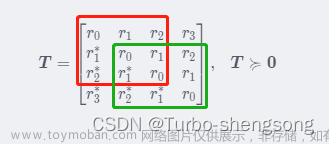
Toeplitz矩阵 的 定义 :Matrices whose entries are constant along each diagonal are called Toeplitz matrices . 形如 T = [ r 0 r 1 r 2 r 3 r − 1 r 0 r 1 r 2 r − 2 r − 1 r 0 r 1 r − 3 r − 2 r − 1 r 0 ] (1) boldsymbol{T}=left[ begin{matrix} r_0 r_1 r_2 r_3\\\\ r_{-1} r_0 r_1 r_2\\\\ r_{-2} r_{-1} r_0 r_1\\\\ r_{-3} r_{-2} r_{-1} r_0\\\\ end{matri
-
矩阵分解(Matrix-Factorization)无门槛
本章主要介绍矩阵分解常用的三种方法,分别为: 1 ◯ textcircled{1} 1 ◯ 特征值分解 2 ◯ textcircled{2} 2 ◯ 奇异值分解 3 ◯ textcircled{3} 3 ◯ Funk-SVD 矩阵分解原理: textbf{large 矩阵分解原理:} 矩阵分解原理: 矩阵分解算法将 m × n mtimes n m × n 维的矩阵 R R R 分解为 m ×
-
最优化方法实验三--矩阵QR分解
1.熟练掌握 QR 分解 Gram–Schmidt方法; 2.掌握 Householder 方 法 ; 3. 能够判断 矩阵是否可逆 ,并 求出其逆矩阵 。 1 .1向量投影 向量的投影包含了两层意思:①正交关系:矢量与投影的差称为误差,误差和投影正交;②最短距离:投影空间中所有矢量中,与原矢量距离最近的,
-
基于opencv的SVD分解求解变换矩阵
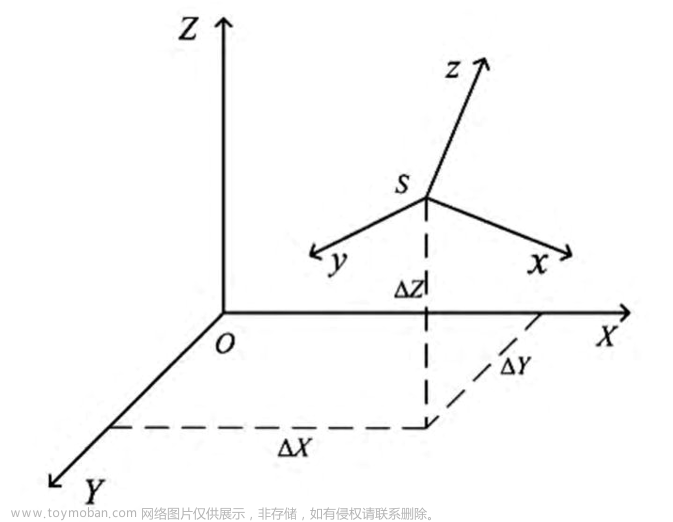
在机器视觉领域,坐标系之间的转换是必不可少的。空间坐标转换的实质是用公共点的两套坐标去推导出两个坐标系之间的转换关系:R(旋转矩阵)和T(平移向量)。 其实点云的配准过程就是求解旋转矩阵R和平移向量T,这里记目标函数为: 式中,n是匹配点个数,假设其最
-
PCA数学原理和非负矩阵分解
于剑老师的教课书太难懂,\\\"PCA主成因分析\\\"这段实在看不懂,还是参考其他老师的文章才基本看懂。 我是搬运工: https://mp.weixin.qq.com/s/Hp1Y1RFH4sxcZjhHuq899A 还要啰嗦一下的是,PCA的理论基础: 根据定义,若x,y独立,则E(xy) = ExEy。若可以将协方差矩阵转换为对角矩阵,那么可以
-
奇异值分解与矩阵逆:数值实现与优化
奇异值分解(Singular Value Decomposition, SVD)和矩阵逆(Matrix Inverse)是线性代数和数值分析领域中非常重要的概念和方法。这两者在现实生活中的应用非常广泛,例如图像处理、信号处理、数据挖掘、机器学习等领域。在这篇文章中,我们将从以下几个方面进行深入的讨论: 背景介绍
-
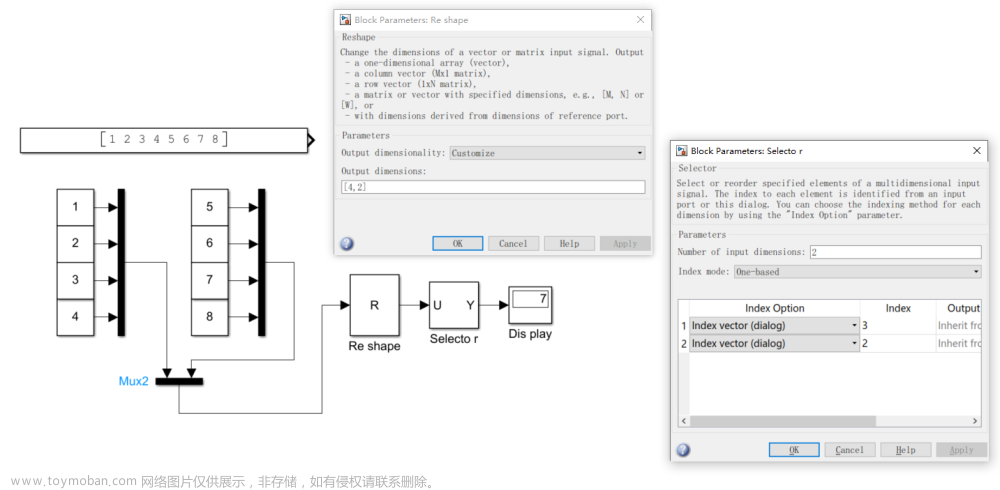
【SIMULINK】simulink实现信号矩阵整合、求逆、转置、分解、向量矩阵相乘(非matlab)
simulink实现信号矩阵,并实现分解 simulink实现信号矩阵求逆 simulink实现信号矩阵转置 simulink矩阵向量相乘
-
【Python】NMF非负矩阵分解算法(测试代码)
欢迎关注 『Python』 系列,持续更新中 欢迎关注 『Python』 系列,持续更新中 从多元统计的观点看,NMF是在非负性的限制下,在尽可能保持信息不变的情况下,将高维的随机模式简化为低维的随机模式H,而这种简化的基础是估计出数据中的本质结构W;从代数的观点看,NMF是