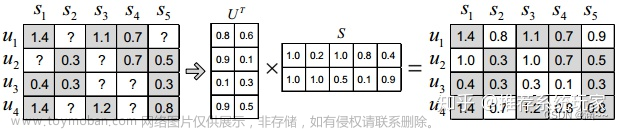
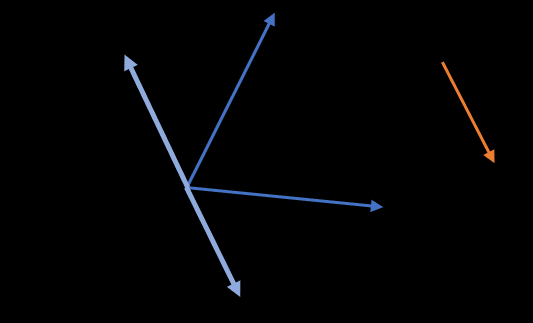
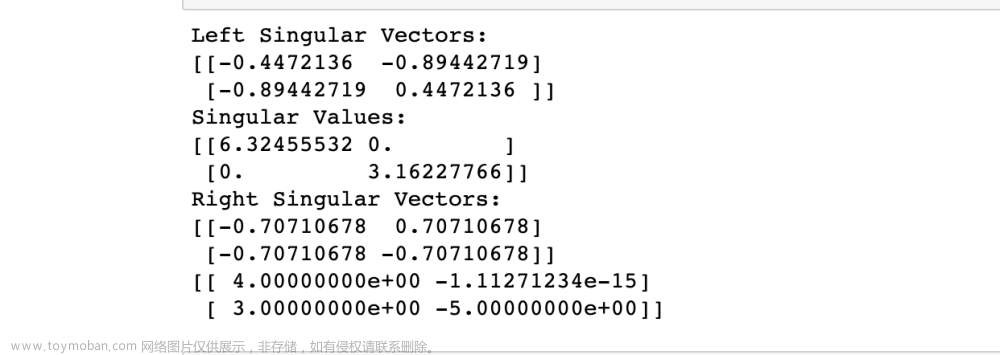
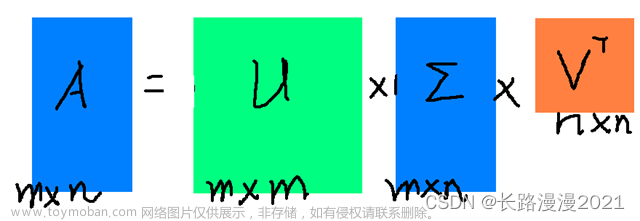
低秩矩阵分解推荐

目录 一·、定义（什么是矩阵分解） 二、矩阵分解的原理 三、矩阵分解的方法 四、矩阵分解的步骤 五、代码实现 六、矩阵分解的优缺点 矩阵分解就是预测出评分矩阵中的缺失值，然后根据预测值以某种方式向用户推荐。常见的矩阵分解方法有基本矩阵分解（basic MF），正

主要是用来记录自己的学习过程，内容也主要来自于网上的各种资料，然后自己总结而来，参考的资料都以注明，感谢这些作者的分享。如果内容有误，请大家指点。 定义        将矩阵等价为两个矩阵 L L L 和 U U U 的乘积 ，其中 L L L 和 U U U 分别是单位下三角矩阵和上三角

Householder变换是一种简洁而有意思的线性变换，也可称为镜面反射变换，Householder变换矩阵为 H = I − w T w H=I-w^Tw H = I − w T w 考虑向量 α alpha α 和一个单位向量 w : w T w = 1 w:w^{T}w=1 w : w T w = 1 α alpha α 在 w w w 方向上的分量是 α w / / = ( w T α ) w = w w T α alpha _{w_{//}}=left( w^{T}

注：本博文为本人阅读论文、文章后的原创笔记，未经授权不允许任何转载或商用行为，否则一经发现本人保留追责权利。有问题可留言联系，欢迎指摘批评，共同进步！！！ 假设矩阵 A mathbf{A} A 是一个 M × N M times N M × N 大小的矩阵。对其进行奇异值分解后可以得到： A

1.1 奇异值分解 奇异值分解（ Singular Value Decomposition，SVD ）是一种重要的矩阵分解技术，它可以将一个矩阵分解为三个矩阵的乘积，分别为左奇异矩阵、奇异值矩阵和右奇异矩阵。SVD 的原理可以描述如下： 对于任意 m × n m times n m × n 的矩阵 A A A ，它的 SVD 分解为： A = U $

前置：线性代数学习笔记3-5：秩1矩阵和矩阵作为“向量”构成的空间 空间 V mathbf V V 有子空间 V 1 mathbf V_1 V 1 ​ （一组基为 α 1 , α 2 , . . . , α k alpha_1,alpha_2,...,alpha_k α 1 ​ , α 2 ​ , ... , α k ​ ）和子空间 V 2 mathbf V_2 V 2 ​ （一组基为 β 1 , β 2 , . . . , β l beta_1,beta_2,

        设 A n × n A_{n times n} A n × n ​ 有 n n n 个线性无关的特征向量 x 1 , … , x n boldsymbol{x}_{1}, ldots, boldsymbol{x}_{n} x 1 ​ , … , x n ​ ，对应特征值分别为 λ 1 , … , λ n lambda_{1}, ldots, lambda_{n} λ 1 ​ , … , λ n ​ A [ x 1 ⋯ x n ] = [ λ 1 x 1 ⋯ λ n x n ] Aleft[begin{array}{lll

单纯矩阵 ：A可对角化⇔①A可对角化；⇔②n个线性无关的特征向量； ⇔③每个特征值的几何重复度等于代数重复度；⇔④特征值λi对应的pi = n - rank(λiE - A)。 等价矩阵 ：A(λ)等价于B(λ)⇔① 任意k阶行列式因子相同Dk(λ)；⇔②有相同的不变因子dk(λ)；⇔③相同的初等因子，且

玩转线性代数(19)初等矩阵与初等变换的相关应用的笔记，例见原文 已知： A r ∼ F A^r sim F A r ∼ F ，求可逆阵 P P P ，使 P A = F PA = F P A = F ( F F F 为 A A A 的行最简形) 方法：利用初等行变换，将矩阵A左边所乘初等矩阵相乘，从而得到可逆矩阵P. 步骤： （1）对矩阵A进行l次初等

LU分解是旨在将某个矩阵表示为两个或多个矩阵的乘积。 LU分解是将矩阵表示为 A A A = L L L U U U ，其中 L L L 矩阵 代表 Lower Triangular（下三角矩阵） ， U U U 矩阵 代表 Upper Triangular（上三角矩阵） 。形象一点就相当于写为 A = ◣ ∗ ◥ A=◣*◥ A = ◣ ∗ ◥ 。 1. 求解U矩阵 先求U矩

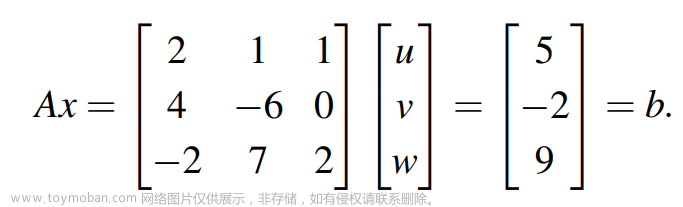
目录 一. 求解Ax=b 二. 上三角矩阵分解 三. 下三角矩阵分解 四. 矩阵的三角分解 举例1：矩阵三角分解 举例2：三角分解的限制 举例3：主元和乘法因子均为1 举例4：U为单位阵 小结 我们知道高斯消元法可以对应矩阵的基础变换。先来看我们比较熟悉的Ax=b模型，如下： 解这个方

1.熟练掌握 QR 分解 Gram–Schmidt方法； 2.掌握 Householder 方 法 ； 3. 能够判断 矩阵是否可逆 ，并 求出其逆矩阵 。 读取附件 MatrixA.mat 文件中的 矩阵 A ， 利用 Gram–Schmidt(GS) 算法对A进行QR分解 。 (1)   验证GS是否 能稳定 进行QR分解矩阵A ，其 Q矩阵 是否正交？ (2) 实现 Householder

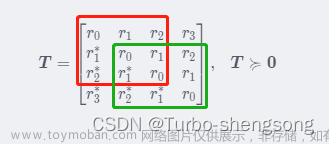
Toeplitz矩阵 的 定义 ：Matrices whose entries are constant along each diagonal are called Toeplitz matrices . 形如 T = [ r 0 r 1 r 2 r 3 r − 1 r 0 r 1 r 2 r − 2 r − 1 r 0 r 1 r − 3 r − 2 r − 1 r 0 ] (1) boldsymbol{T}=left[ begin{matrix} r_0 r_1 r_2 r_3\\\\ r_{-1} r_0 r_1 r_2\\\\ r_{-2} r_{-1} r_0 r_1\\\\ r_{-3} r_{-2} r_{-1} r_0\\\\ end{matri

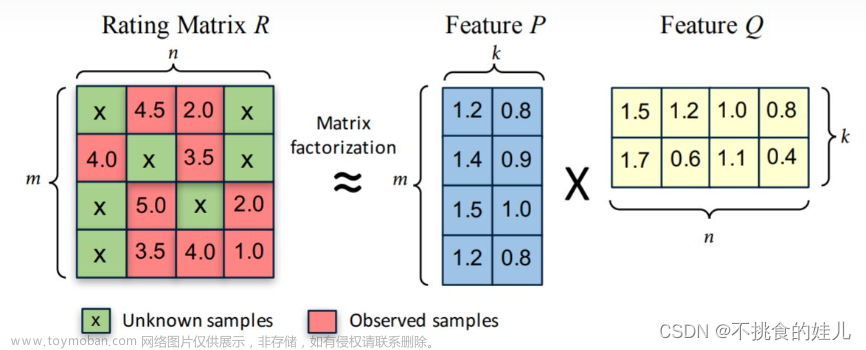
本章主要介绍矩阵分解常用的三种方法，分别为： 1 ◯ textcircled{1} 1 ◯ 特征值分解 2 ◯ textcircled{2} 2 ◯ 奇异值分解 3 ◯ textcircled{3} 3 ◯ Funk-SVD 矩阵分解原理： textbf{large 矩阵分解原理：} 矩阵分解原理：   矩阵分解算法将 m × n mtimes n m × n 维的矩阵 R R R 分解为 m ×

1.熟练掌握 QR 分解 Gram–Schmidt方法； 2.掌握 Householder 方 法 ； 3. 能够判断 矩阵是否可逆 ，并 求出其逆矩阵 。 1 .1向量投影 向量的投影包含了两层意思：①正交关系：矢量与投影的差称为误差，误差和投影正交；②最短距离：投影空间中所有矢量中，与原矢量距离最近的，