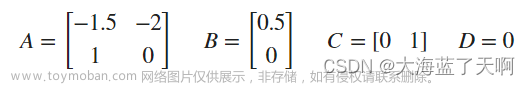求矩阵的秩的代码
-
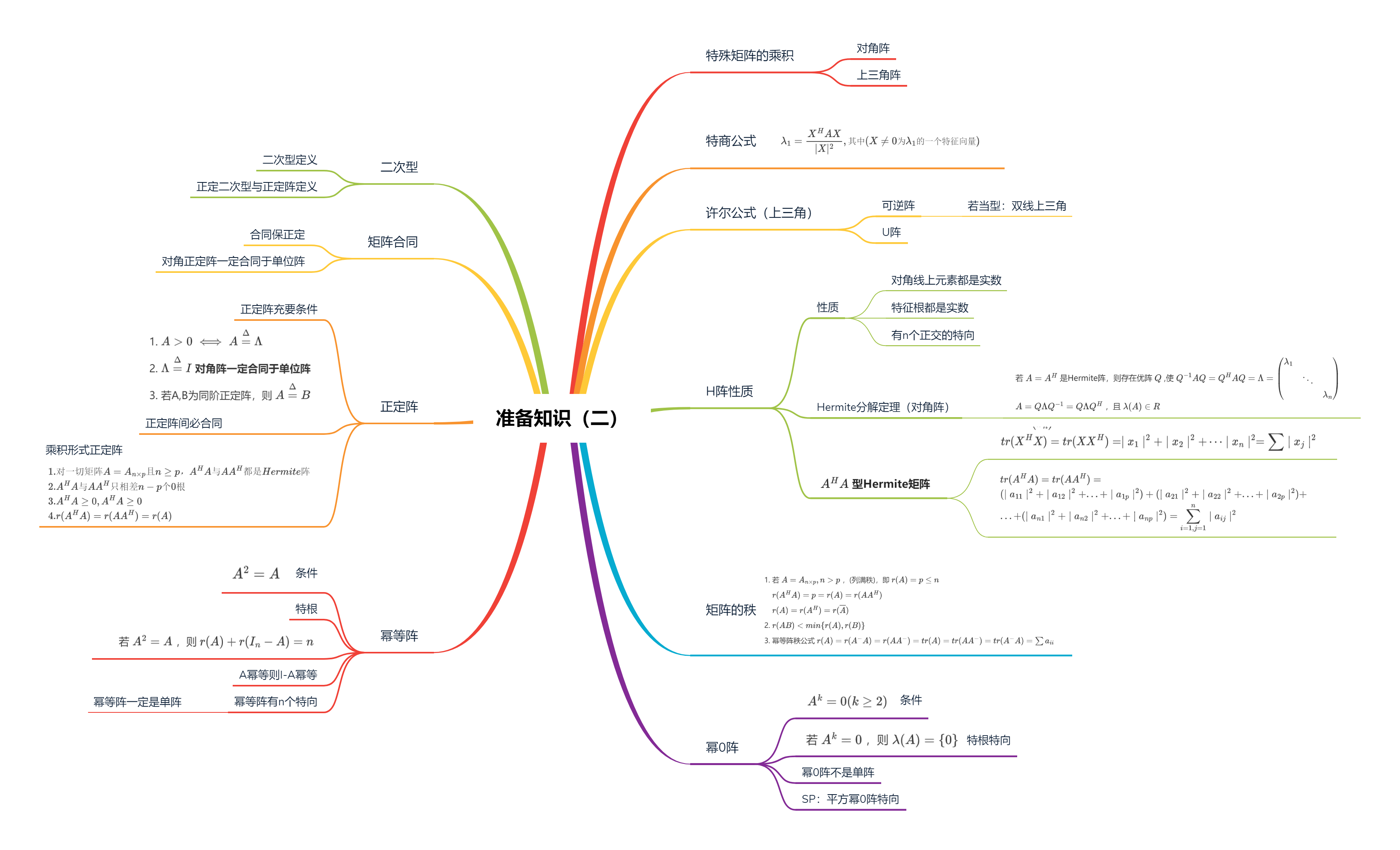
【矩阵论】1.准备知识——Hermite阵,二次型,矩阵合同,正定阵,幂0阵,幂等阵,矩阵的秩
矩阵论的所有文章,主要内容参考北航赵迪老师的课件 [注]由于矩阵论对计算机比较重要,所以选修了这门课,但不是专业搞数学的,所以存在很多口语化描述,而且对很多东西理解不是很正确与透彻,欢迎大家指正。我可能间歇性忙,但有空一定会回复修改的。 矩阵论 1
-
解密Python求矩阵秩的算法与实用指南:从基础到高阶方法
在线性代数和计算机科学中,矩阵秩是一个重要的概念,它反映了矩阵中线性无关的行或列的数量,从而揭示了矩阵的重要性质。Python 作为一门强大的编程语言,提供了多种方法来求解矩阵的秩。本文将深入探讨 Python 中求解矩阵秩的算法,从基础的高斯消元法到高阶的 SV
-
【考研数学】线形代数第三章——向量 | 3)向量秩的性质、向量空间、过渡矩阵
紧接前文学习完向量组秩的基本概念后,继续往后学习向量的内容。 性质 1(三秩相等) —— 设 A = ( β 1 , β 2 , … , β n ) = ( α 1 , α 2 , … , α n ) T pmb{A=(beta_1,beta_2,dots,beta_n)=(alpha_1,alpha_2,dots,alpha_n)^T} A = ( β 1 , β 2 , … , β n ) = ( α 1 , α 2 , … , α n )
-
【线代】矩阵的秩和线性方程组的解的情况
行最简型矩阵 :(也可以叫做行最简阶梯型矩阵,或者行简化阶梯型矩阵),其特点是:非零行的首非零元为1,且这些非零元所在的列的其它元素都为0。所谓的行最简的意思就是对应的方程组是“最简单的”,就是说,对应的方程组,最多只需要移项就行了,不再需要其他任何
-
线性方程组系数矩阵的秩与解的个数的关系
齐次方程组: A x = 0 Ax=0 A x = 0 系数矩阵 A n × n A_{n×n} A n × n 的秩 解的个数 满秩: r ( A ) = n r(A)=n r ( A ) = n 仅有零解 不满秩: r ( A ) = r n r(A)=rn r ( A ) = r n 有无穷多解 注: 齐次线性方程 A x = 0 Ax=0 A x = 0 一定有解. 当 r ( A ) = r n r(A)=rn r ( A ) = r n 时, 基础解系 (线性无关的
-
【算法竞赛模板】求解线性方程组是否有解(求解矩阵的秩)
在实际运用中需判断线性方程组有无解,可以通过矩阵运算判断线性方程组是否有解 线性方程组有无解总结: 矩阵求解秩流程: 所以:当我们遇到题目问线性方程组是否有解时,只需求解系数矩阵的秩与增广矩阵的秩的关系 。我们可以通过分别求系数矩阵与增
-
【考研数学】线形代数第三章——向量 | 3)向量组秩的性质、向量空间、过渡矩阵
紧接前文学习完向量组秩的基本概念后,继续往后学习向量的内容。 性质 1(三秩相等) —— 设 A = ( β 1 , β 2 , … , β n ) = ( α 1 , α 2 , … , α n ) T pmb{A=(beta_1,beta_2,dots,beta_n)=(alpha_1,alpha_2,dots,alpha_n)^T} A = ( β 1 , β 2 , … , β n ) = ( α 1 , α 2 , … , α n )
-
6.利用matlab完成 符号矩阵的秩和 符号方阵的逆矩阵和行列式 (matlab程序)
1. 简述 利用 M 文件建立矩阵 对于比较大且比较复杂的矩阵,可以为它专门建立一个 M 文件。下面通过一个简单例子来说明如何利用 M 文件创建矩阵。 例 2-2 利用 M 文件建立 MYMAT 矩阵。 (1) 启动有关编辑程序或 MATLAB 文本编辑器,并输入待建矩阵: (
-
MATLAB中对方阵行列式的求解、矩阵的累加和与累乘积进行求解、矩阵的排序、矩阵的秩和迹、以及矩阵的特征值和特征向量的求解
目录 1、方阵的行列式计算 2、累加和与累乘积 (1)累加和 (2)累乘积 3、对于数据进行排序 4、求矩阵的秩 5、矩阵的迹 6、计算矩阵的特征值和特征向量 在线性代数中,对于一个方阵进行求值运算需要先将其转换为行列式,MATLAB中提供过了det函数用于对于方阵的行列式进
-
matlab函数 状态空间系统ss、能控性矩阵ctrb、矩阵的秩rank、能控标准型canon、零极点配置place、系统极点pole等函数(线性定常系统)
如果已知线性定常系统的ABCD四个矩阵,可以得到状态空间系统 其他更具体的用法请直接看帮助文档。 用法:ss(A,B,C,D) 假如 可以输入 最后得到 判断系统是否能控,可以用能控性矩阵是否奇异进行判断。ctrb函数用来生成能控性矩阵,rank用来判断矩阵的秩 对于线性定常系统
-
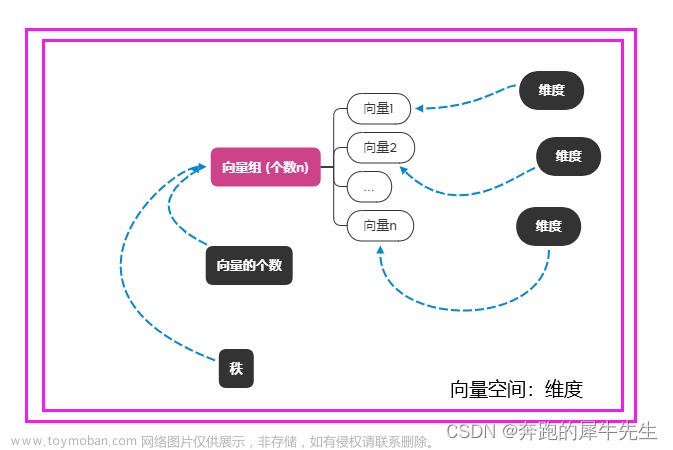
线性代数的学习和整理18:什么是维度,什么是秩?秩的各种定理&&秩的计算 (计算部分未完成)
目录 0 问题引出:什么是秩? 概念备注: 1 先厘清:什么是维数? 1.1 真实世界的维度数 1.2 向量空间的维数 1.2.1 向量空间,就是一组最大线性无关的向量组/基张成的空间 1.3 向量α的维数 1.3.1 向量的维数=分量(数字/标量)个数 1.4 向量组/矩阵 A 的维数 1.4.1 什么是向量组的维
-
有关秩的结论。
序号 结论 1. r(A) = A的列秩 = A的列秩 2. 若A可逆,则r(AB)=r(B),r(BA)=r(B) 3. 若A是mXn矩阵,B是nXs矩阵,且AB=O,则r(A)+r(B)=n 序号 设A是Mxn矩阵,B是满足有关矩阵要求的矩阵 4. 0= A = min{m,n} 5. r(kA) = r(A)(k/=0) 6. r(AB) = min{r(A),r(B)} 7. r(A+B)= r(A) +r(B) 前序:先引入矩阵如下性质 : 由上述矩阵兴致明
-
秩和检验(秩的概念,秩和检验法)
设有两个总体,它们的概率密度分别为 ,有 ,有如下假设 设两个总体均值存在,分别为 ,则以上假设就等价于以下假设 设一总体X,有容量为n的样本,从小到大排列为 ,..., , 的下标就是它的秩。 例如12333445其中33的秩就是2 如果有相等的数,它们的秩就为它们的下标的平均
-
线性代数:向量组的秩
目录 回顾“秩” 及 向量组线性表示 相关特性 向量组的秩 例1 例2
-
数字流的秩、单词频率(哈希实现)
题目1:数字流的秩 假设你正在读取一串整数。每隔一段时间,你希望能找出数字 x 的秩(小于或等于 x 的值的个数)。请实现数据结构和算法来支持这些操作,也就是说: 实现 track(int x) 方法,每读入一个数字都会调用该方法; 实现 getRankOfNumber(int x) 方法,返回小于或等于
-
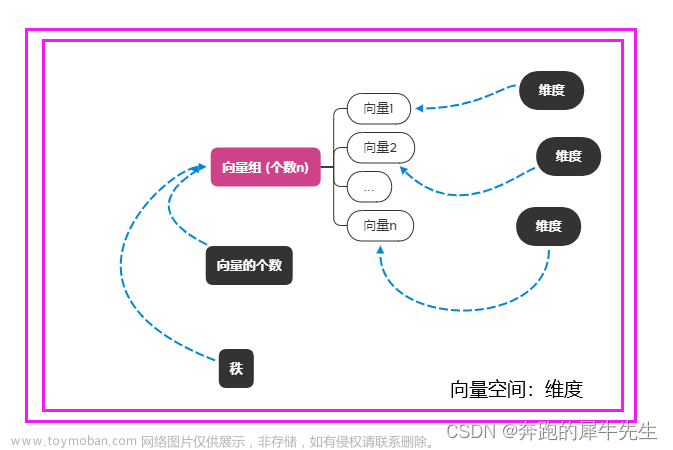
线性代数的学习和整理18:什么是维度,什么是秩?关于秩的各种定理 (未完成)
目录 0 问题引出:什么是秩? 概念备注: 1 先厘清:什么是维数? 1.1 真实世界的维度数 1.2 向量空间的维数 1.2.1 向量空间,就是一组最大线性无关的向量组/基张成的空间 1.3 向量α的维数 1.3.1 向量的维数=分量(数字/标量)个数 1.4 向量组/矩阵 A 的维数 1.4.1 什么是向量组的维
-
C++两个矩阵相乘代码(内附有矩阵相乘的条件与规则,以及对代码的详细解答)
再复制粘贴代码之前可以先了解学习一下什么是矩阵相乘,矩阵相乘的条件与规则又是什么。 点击一下链接即可进入学习: #矩阵相乘的学习链接 以下是两个矩阵相乘的代码块(输入版) 补充①:对于for循环了解还不够透彻的可以进
-
python矩阵乘法全面解读,python矩阵乘法常用代码
矩阵乘法,顾名思义是矩阵的乘法,矩阵相乘的含义是两个向量的积,在 Python中一般以乘号或括号表示。与常用的加、减、乘、除运算不同,矩阵乘法只能用于对给定矩阵进行乘法运算,不能进行除法运算。若要计算矩阵乘法的值,必须先进行矩阵分解。 在上一篇文章中
-
空间权重矩阵构建(Stata代码)
整理了一下几个空间权重矩阵生成的Stata代码,小伙伴们仅供参考哈。
-
如何保存矩阵?python代码实现
机器学习中的参数矩阵如何保存??当脱离了dl的框架后,菜鸟表示啥都不会。。 可以借用scipy包的savemat函数保存,loadmat函数读取; 首先要确保有scipy这个包,没有就安装一下 pip install scipy ,我这里的版本是1.7; Talk is cheap ,show me the code~ 第二种实现方式: #利用pickle实现,代