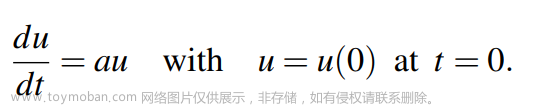矩阵特征值分解
-
线性代数(四) 特征值&相似矩阵
前面主要讲述的是方程组和矩阵的关系,现在了解下矩阵和矩阵的关系 假设A为n阶方阵,对于一个数 λ lambda λ 若存在:非零列向量 α alpha α ,使得: A α ⃗ = λ α ⃗ Avec{alpha}=lambdavec{alpha} A α = λ α λ lambda λ 叫做矩阵A的一个特征值 α ⃗ vec{alpha} α 叫做对应特征值的
-
Python中的矩阵对角化与特征值、特征向量
Python中的矩阵对角化与特征值、特征向量 在数学和物理学中,矩阵对角化是一种重要的矩阵变换方法。Python提供了许多工具和库来实现矩阵对角化操作,并能够计算矩阵的特征值和特征向量。本文将针对Python中的矩阵对角化、特征值和特征向量的相关概念进行详细的介绍。
-
线性代数|证明:矩阵不同特征值对应的特征向量线性无关
定理 1 设 λ 1 , λ 2 , ⋯ , λ m lambda_1,lambda_2,cdots,lambda_m λ 1 , λ 2 , ⋯ , λ m 是方阵 A boldsymbol{A} A 的 m m m 个特征值, p 1 , p 2 , ⋯ , p m boldsymbol{p}_1,boldsymbol{p}_2,cdots,boldsymbol{p}_m p 1 , p 2 , ⋯ , p m 依次是与之对应的特征向量,如果 λ 1 , λ 2 , ⋯ , λ
-
【线性代数】矩阵特征值的快速求法
本文讨论 3阶矩阵 的特征值的快速求法。 分为速写特征多项式和速解方程两部分。 速写特征多项式 不妨令: A = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] boldsymbol{A}=left[begin{array}{lll} a_{11} a_{12} a_{13} \\\\ a_{21} a_{22} a_{23} \\\\ a_{31} a_{32} a_{33} end{array}right] A = a 11 a 21 a 31
-
实对称矩阵的奇异值等于特征值
首先,来看一下什么叫作矩阵的奇异值,根据课本上的定义 1 定理1: 实对称矩阵的奇异值等于其特征值. 证明: 对于实对称矩阵 A A A , 其特征值为 λ 1 , λ 2 , . . . , λ n lambda_1,lambda_2,...,lambda_n λ 1 , λ 2 , . . . , λ n . 由某个定理可知(自己查找一下), A 2 A^2 A 2 的特
-
利用矩阵特征值解决微分方程【1】
目录 一. 特征值介绍 二. 单变量常微分方程 三. 利用矩阵解决微分方程问题 四. 小结 4.1 矩阵论 4.2 特征值与特征向量内涵 4.3 应用 线性代数有两大基础问题: 如果A为对角阵的话,那么问题就很好解决。需要注意的是,矩阵的基础行变换会改变特征值的大小。 在已知解的情况
-
雅可比旋转(Jacobi法)求对称矩阵的特征值和特征向量
该方法是求解 对称矩阵 全部特征值和特征向量的一种方法,它基于以下结论: ① 任何实对称矩阵A可以通过正交相似变换成对角型 ,即存在正交矩阵Q,使得 Q T A Q = d i a g ( λ 1 , λ 2 , … , λ n ) Q^TAQ=diag(λ1,λ2,…,λn) Q T A Q = d ia g ( λ 1 , λ 2 , … , λn ) 其中λi(i=1,2,…,n)是A的特征
-
MATLAB 构建协方差矩阵,解算特征值和特征向量(63)
对于某片有待分析的点云,我们希望构建协方差矩阵,计算特征值和特征向量,这是很多算法必要的分析方法,这里提供完整的计算代码(验证正确) !!! 特别需要注意的是:特征值的排序方式 这里计算的特征值按照从小到大的顺序重新排列得到:L1 L2 L3,这样每个特征值都
-
矩阵AB和BA的特征值相同
手写的,如下图: 即可证明,矩阵AB的特征值和BA的特征值相同。 关于矩阵转置和逆矩阵混合运算,有如下规律:
-
特征值与特征向量:矩阵的对称性与非对称性
在现实生活中,我们经常会遇到各种各样的问题,这些问题通常可以用数学模型来描述。在数学中,矩阵是一个非常重要的概念,它可以用来描述各种各样的问题。在本文中,我们将讨论矩阵的对称性与非对称性,以及如何通过计算特征值和特征向量来解决这些问题。 矩阵是
-
证明矩阵特征值之积等于矩阵行列式的值
设n阶矩阵 A A A 的特征值为 λ 1 , λ 2 , . . , λ n lambda_1, lambda_2,..,lambda_n λ 1 , λ 2 , .. , λ n ,则 λ 1 λ 2 ⋯ λ n = ∣ A ∣ 。 lambda_1lambda_2cdotslambda_n = |A|。 λ 1 λ 2 ⋯ λ n = ∣ A ∣ 。 证明: 矩阵 A A A 的特征多项式为: f ( λ ) = ∣ λ E − A ∣ = ∣ λ − a 11 −
-
矩阵的范数和特征值之间的关系
参考: linear algebra - Why is the norm of a matrix larger than its eigenvalue? - Mathematics Stack Exchange
-
【证明】矩阵特征值之和等于主对角线元素之和
性质 1 设 n n n 阶矩阵 A = ( a i j ) boldsymbol{A} = (a_{ij}) A = ( a ij ) 的特征值为 λ 1 , λ 2 , ⋯ , λ n lambda_1,lambda_2,cdots,lambda_n λ 1 , λ 2 , ⋯ , λ n ,则 λ 1 + λ 2 + ⋯ + λ n = a 11 + a 22 + ⋯ + a n n lambda_1 + lambda_2 + cdots + lambda_n = a_{11} + a_{22} + cdots + a_{nn} λ 1 + λ 2
-
向量与矩阵 导数和偏导数 特征值与特征向量 概率分布 期望方差 相关系数
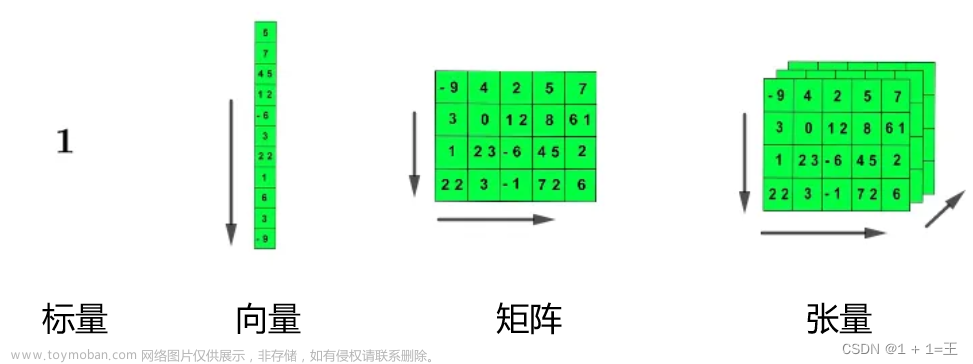
标量(scalar) :一个单独的数。 向量(vector) :⼀组有序排列的数。通过次序中的索引,我们可以确定每个单独的数。 矩阵(matrix) :具有相同特征和纬度的对象的集合。⼀个对象表⽰为矩阵中的⼀⾏,⼀个特征表⽰为矩阵中的⼀列,表现为⼀张⼆维数据表。 张量(ten
-
线性代数的学习和整理19,特征值,特征向量,以及引入的正交化矩阵概念
目录 1 什么是特征值和特征向量? 1.1 特征值和特征向量这2个概念先放后 1.2 直观定义 1.3 严格定义 2 如何求特征值和特征向量 2.1 方法1:结合图形看,直观方法求 2.1.1 单位矩阵的特征值和特征向量 2.1.2 旋转矩阵 2.2 根据严格定义的公式 A*X=λ*X 来求 2.3 特征方程 2.4 互异特
-
谈主成分分析/因子分析中的特征值“矩阵近似”
主成分分析和因子分析是数据降维的常用手段,其中以特征值为载体,在不断降维“近似”原本的协方差矩阵。 CSDN中一些文章在介绍这个问题或者叫“特征值分解”时,讲得都比较学术化,今天用一个小例子,还是面向新人,来引导理解“特征值分解”和“矩阵近似”(图
-
线性代数|证明:矩阵特征值之积等于矩阵行列式的值
性质 1 设 n n n 阶矩阵 A = ( a i j ) boldsymbol{A} = (a_{ij}) A = ( a ij ) 的特征值为 λ 1 , λ 2 , ⋯ , λ n lambda_1,lambda_2,cdots,lambda_n λ 1 , λ 2 , ⋯ , λ n ,则 λ 1 λ 2 ⋯ λ n = ∣ A ∣ lambda_1 lambda_2 cdots lambda_n = |boldsymbol{A}| λ 1 λ 2 ⋯ λ n = ∣ A ∣ 。 证明 不妨设
-
【数值分析】用幂法计算矩阵的主特征值和对应的特征向量(附matlab代码)
用幂法计算下列矩阵的按模最大特征值及对应的特征向量 k= 1 V^T= 8 6 0 m= 8 u^T= 1.0000 0.7500 0 k= 2 V^T= 9.2500 6.0000 -2.7500 m= 9.2500 u^T= 1.0000 0.6486 -0.2973 k= 3 V^T= 9.5405 5.8919 -3.5405 m= 9.5405 u^T= 1.0000 0.6176 -0.3711 k= 4 V^T= 9.5949 5.8414 -3.7309 m= 9.5949 u^T= 1.0000 0.6088 -0.3888 k= 5 V^T= 9.6041 5.8240 -3.7753 m=
-
线性代数|证明:矩阵特征值之和等于主对角线元素之和
性质 1 设 n n n 阶矩阵 A = ( a i j ) boldsymbol{A} = (a_{ij}) A = ( a ij ) 的特征值为 λ 1 , λ 2 , ⋯ , λ n lambda_1,lambda_2,cdots,lambda_n λ 1 , λ 2 , ⋯ , λ n ,则 λ 1 + λ 2 + ⋯ + λ n = a 11 + a 22 + ⋯ + a n n lambda_1 + lambda_2 + cdots + lambda_n = a_{11} + a_{22} + cdots + a_{nn} λ 1 + λ 2
-
【OpenCV4】计算对称矩阵特征值和特征向量 cv::eigen() 用法详解和代码示例(c++)
解析: src:输入矩阵,只能是 CV_32FC1 或 CV_64FC1 类型的方阵(即矩阵转置后还是自己) eigenvalues:输出的特征值组成的向量,数据类型同输入矩阵,排列从大到小 eigenvectors:输出的特征向量组成的矩阵,数据类型同输入矩阵,每一行是一个特征向量,对应相应位置的特征值