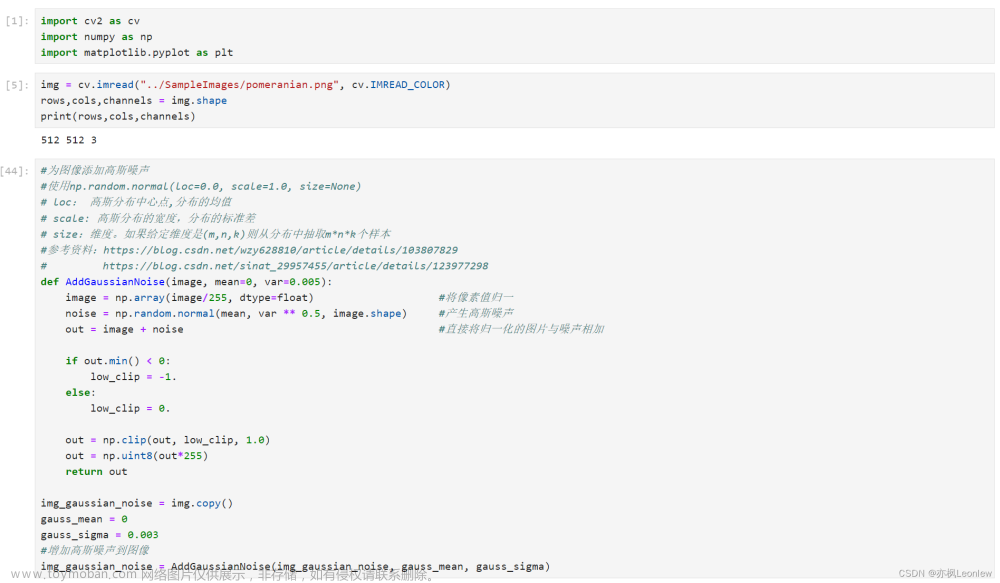
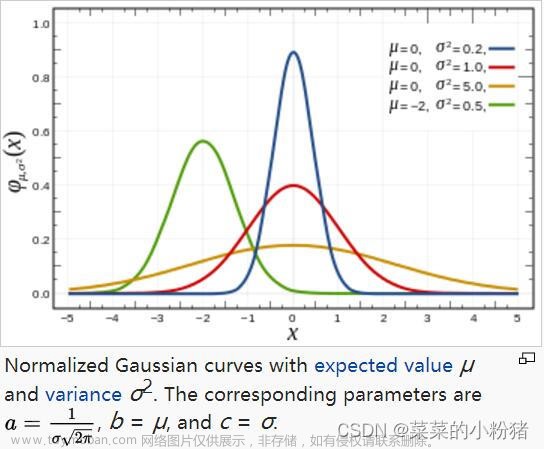
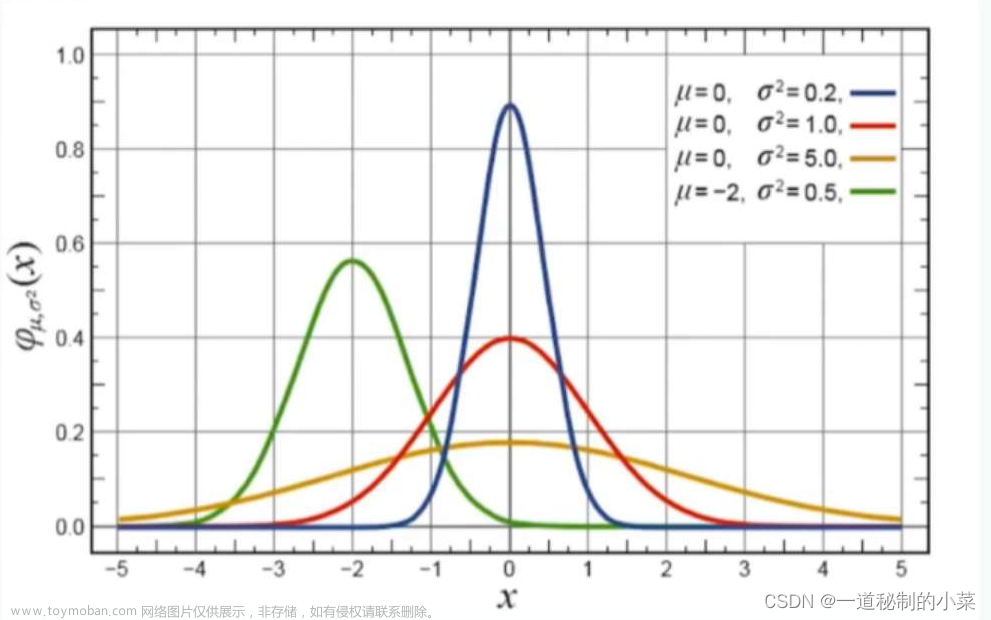
矩阵的高斯随机化
-
Google Earth Engine(GEE)——土地分类精度分析randomColumn产生伪随机数然后进行混淆矩阵计算
我们在进行土地分类时,需要进行精度验证,但是之前我们要进行样本点的随机分类,也就是分出一部分作为训练样本另外一部分作为,这是我们要想产生随机种子赋值给我们所选定的训练样本,这样我们就可以随机将样本进行分成训练样本和验证样本,而我们使用的函数
-
#MATLAB 利用基本矩阵产生3x3和15x8的单位阵,全1阵,全0阵,均匀分布的随机阵([-1,1]之间),正态分布随机阵(方差4,均值1)
利用基本矩阵产生3x3和15x8的单位阵,全1阵,全0阵,均匀分布的随机阵([-1,1]之间),正态分布随机阵(方差4,均值1) 题解: 输出: a1 = 1 0 0 0 1 0 0 0 1 a2 = 1 0 0 0 0 0 0 0
-
#MATLAB 产生一均匀分布在(-5,5)随机阵(50x2),精确到小数点后一位,并判断该矩阵中是否含有0元素
产生一均匀分布在(-5,5)随机阵(50x2),精确到小数点后一位,并判断该矩阵中是否含有0元素 题解: 输出示例1: a = -3.9000 3.8000 -0.4000 3.5000 2.2000 4.8000 -4.8000 -4.6000 4.6000 -4.7000 1.7000 3.8000 -4.7000 0.3000 1.3000 -1.
-
概率,概率分布,高斯分布,高维高斯分布
高斯分布的理解, 它在低维和高维的形式。 两个基本的概念: 概率:在某事件出现某一结果的可能性大小。 分布:考虑事件的所有可能性 那么它就是分布。 分布函数,是概率统计中重要的函数,正是通过它,可用数学分析的方法来研究随机变量。分布函数是随机变量最重要的概
-
机器学习笔记之高斯网络(二)高斯贝叶斯网络
上一节介绍了 高斯网络 及其条件独立性,本节将介绍 高斯贝叶斯网络 。 高斯网络 高斯网络最核心的特点是: 随机变量集合中的随机变量均是连续型随机变量,并且均服从高斯分布 : 已知某随机变量集合 X mathcal X X 中包含 p p p 个特征,整个 高斯网络 中所有结点的 联合
-
高斯分布、高斯混合模型、EM算法详细介绍及其原理详解
K近邻算法和KD树详细介绍及其原理详解 朴素贝叶斯算法和拉普拉斯平滑详细介绍及其原理详解 决策树算法和CART决策树算法详细介绍及其原理详解 线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解 硬间隔支持向量机算法、软间隔支持向量机算法、非线性支持向量机算
-
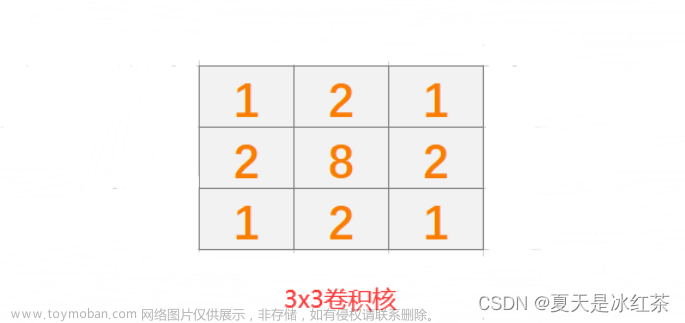
图像处理:高斯滤波算法
目录 前言 概念介绍 基本原理 卷积核的大小 卷积核的形状和权重比 卷积核的归一化 结论 Opencv实现高斯滤波 Python手写实现高斯滤波 参考文章 在此之前,我曾在此篇中推导过图像处理:推导五种滤波算法(均值、中值、高斯、双边、引导)。这在此基础上,我想更深入地研
-
01:高斯噪声和椒盐噪声
记录一下手写椒盐噪声和高斯噪声的python程序。 效果图如下: 椒盐噪声和高斯噪声都是数字图像处理中常见的噪声类型。 1.椒盐噪声是 随机的黑色和白色像素点 混杂在图像中,使得图像中的一些像素点变得十分明显且不规则。椒盐噪声可能由于传感器损坏、传输错误、压缩
-
模式识别——高斯分类器
所有问题定义在分类问题下,基于贝叶斯决策 条件概率为多元高斯分布,此时观测为向量 X = X 1 , X 2 , . . . , X n X={X_1,X_2,...,X_n} X = X 1 , X 2 , ... , X n ,通过极大后验展开可以得到最优决策函数: 决策函数可以写为: d d d 就是马氏距离,代表两个高斯分布之间的距离。
-
高斯分布的乘积与卷积
高斯分布作为一种重要的连续分布形式,频繁出现在各种应用场景里,典型如卡尔曼滤波器的设计与计算中涉及两个高斯分布的乘积,计算符合高斯分布的两个独立随机变量和的概率密度函数涉及高斯分布的卷积。 令,均是关于变量的高斯分布,现计算高斯分布的乘积的分布
-
高斯滤波及其原理
1.1 期望、方差与标准差 用来刻画随机变量某一方面特征的常数被称为随机变量的数字特征,其常用的有: 数学期望 : 在概率论和统计学中,数学期望(mean)是试验中每次可能结果的 概率 乘以其 结果 的总和,是最基本的数学特征之一。它反映随机变量 平均取值 的大小
-
对数高斯分布
对数高斯分布是指服从正态分布的随机变量经过取对数变换后得到的分布。具体地,设 X ∼ N ( μ , σ 2 ) Xsim N(mu,sigma^2) X ∼ N ( μ , σ 2 ) 为一个正态分布随机变量, Y = ln ( X ) Y=ln(X) Y = ln ( X ) 则 Y Y Y 服从对数高斯分布,即 Y ∼ L N ( μ , σ 2 ) Ysimmathcal{LN}(mu,sigma^2) Y ∼
-
图像处理之高斯滤波
高斯函数广泛应用于统计学领域,用于表述正态分布,在信号处理领域,用于定义高斯滤波器,在图像处理领域,二维高斯核函数常用于高斯模糊Gaussian Blur,在数学领域,主要是用于解决热力方程和扩散方程,以及定义Weiertrass Transform。 高斯函数,Gaussian Function, 也简称为
-
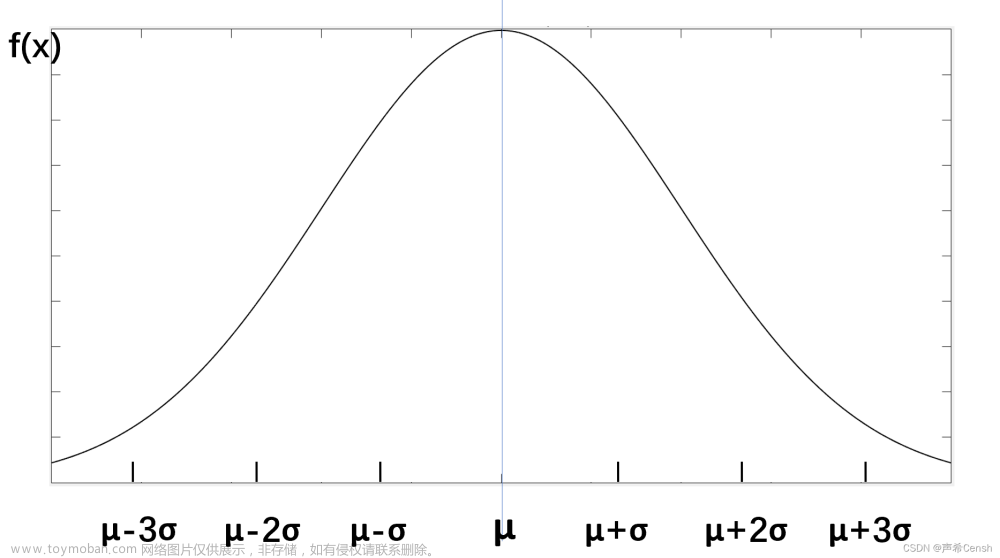
OpenCV-22高斯滤波
要理解高斯滤波首先要直到什么是高斯函数,高斯函数是符合高斯分布的(也叫正态分布)的数据的概率密度函数。 高斯函数的特点是以x轴某一点(这一点称为均值)为对称轴,越靠近中心数据发生的概率越高,最终形成一个两边平缓,中间陡峭的钟型(有的地方也叫帽子
-
opencv的高斯滤波函数
//1、高斯滤波器 GaussianBlur(NormalX, res1, Size(Ksize, Ksize), Sigma); //2、高斯分离卷积 Mat v = getGaussianKernel(Ksize, Sigma); sepFilter2D(NormalX, res2, -1, v.t(), v); //3、普通卷积 filter2D(NormalX, res3, -1, v*v.t()); 结论: (1)当都是高斯核的时候,三者结
-
列主高斯消元法
看过我前几个博文的小伙伴们,细心的小伙伴会发现我前面讲过一个 高斯消元法 ,那么和接下来讲的列主高斯消去法有什么区别呢?? 目录 一、前言 二、列主高斯消元法 1.数学计算过程 三、代码实现过程 1、源代码展示(这次没有采用高斯消元法中校园的时候,进阶的列
-
高斯滤波器
最近读论文和看源码过程中经常看到高斯滤波器这个概念,论文中说的是利用高斯滤波器来进行去噪、使得特征变得光滑啥的,就不免有一个疑问,为啥高斯滤波器这么牛?同时高斯滤波器也可以看作一种特殊的卷积,那么研究一下高斯滤波器也将有助于我们理解CNN。 图像噪
-
高斯消元法(matlab)
目录 高斯部分主元消元法 高斯列主元消元法 高斯部分主元消去法: 原理:将线性方程组的系数即为矩阵A(n,n),对应的值即为 B(n,1),记增广矩阵C为(A,B); 第一步:找出系数中绝对值最大的元素,将其交换到C(1,1),通过线性运算,使得第一列C(1,1)下面的元素都消为0; 第二步
-
高斯噪声(Gaussian noise)
高斯噪声,也称为白噪声或随机噪声,是一种符合高斯(正态)分布的随机信号或干扰。它的特点是在所有频率上具有恒定的功率谱密度,使其在不同频率上呈现出等能量的随机波动。 从实际角度来看,高斯噪声是指在各种系统和过程中发生的随机变化或扰动。它存在于许多