秩和检验和卡方检验的区别
-
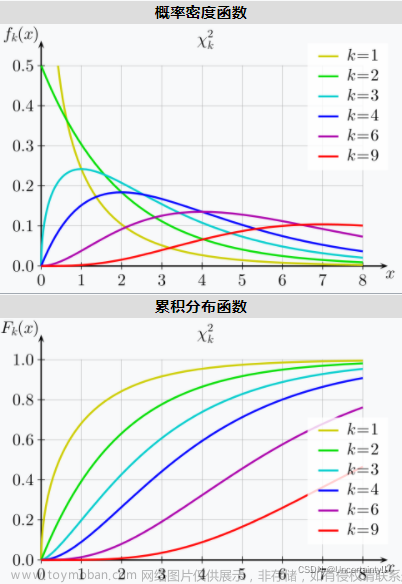
卡方分布(Chi-Square Distribution)
在统计学中, 很多假设检验的检验统计量在原假设下服从卡方分布. 这种检验统计量服从卡方分布的假设检验适用于分类数据. Γ ( v 2 ) Gamma(frac{v}{2}) Γ ( 2 v ) 为伽马函数 检验此PDF的积分值是否为1? 自由度 (DoF)的正式定义为统计学中可以自由变化的数值个数. 如果有 N
-
【分布族谱】卡方分布和F分布之间的关系
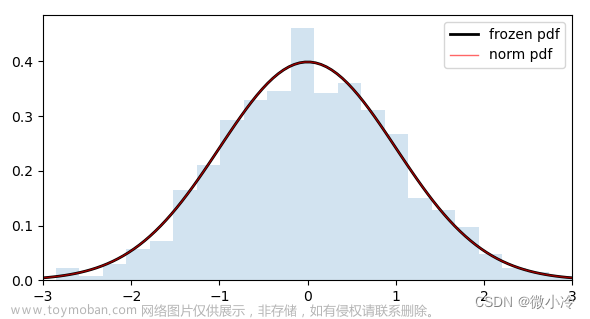
正态分布,最早由棣莫弗在二项分布的渐近公式中得到,而真正奠定其地位的,应是高斯对测量误差的研究,故而又称Gauss分布。。测量是人类定量认识自然界的基础,测量误差的普遍性,使得正态分布拥有广泛的应用场景,或许正因如此,正太分布在分布族谱图中居于核心
-
三大抽样分布:卡方分布,t分布和F分布
定义: 卡方检验 :卡方检验主要用于分类变量之间的独立性检验 基本思想 :卡方表示观察值与理论值之间的偏离程度 。 定义: 应用: t -分布 ( t -distribution)用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知
-
线性代数的学习和整理18:矩阵的秩的各种定理, 秩和维度(未完成)
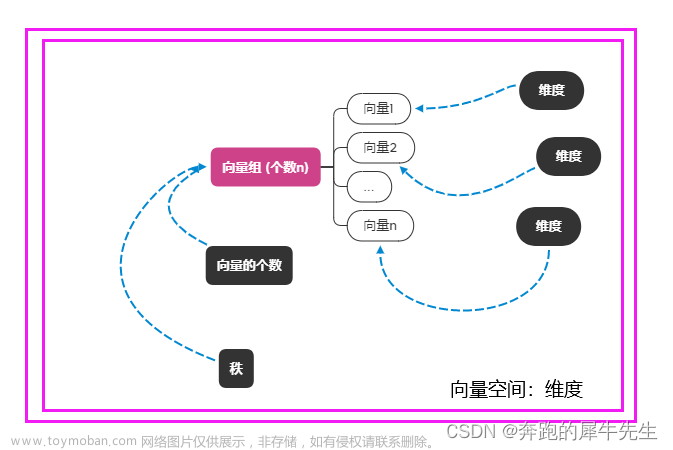
目录 0 问题引出:什么是秩? 概念备注: 1 先厘清:什么是维数? 1.1 真实世界的维度数 1.2 向量空间的维数 1.2.1 向量空间,就是一组最大线性无关的向量组/基张成的空间 1.3 向量α的维数 1.3.1 向量的维数=分量(数字/标量)个数 1.4 向量组/矩阵 A 的维数 1.4.1 什么是向量组的维
-
简述矩阵的秩和向量组的秩的定义 从定义出发分析两者之间的相互关系
(1)简述矩阵的秩和向量组的秩的定义;(2)从定义出发分析两者之间的相互关系。 (1)简述矩阵的秩和向量组的秩的定义: 矩阵的秩的定义:设在矩阵A中有一个不为0的r阶子式D,且所有的r+1阶子式(若存在)全为0,则D称为矩阵A的最高阶非零子式,它的阶数r称为矩阵
-
6.利用matlab完成 符号矩阵的秩和 符号方阵的逆矩阵和行列式 (matlab程序)
1. 简述 利用 M 文件建立矩阵 对于比较大且比较复杂的矩阵,可以为它专门建立一个 M 文件。下面通过一个简单例子来说明如何利用 M 文件创建矩阵。 例 2-2 利用 M 文件建立 MYMAT 矩阵。 (1) 启动有关编辑程序或 MATLAB 文本编辑器,并输入待建矩阵: (
-
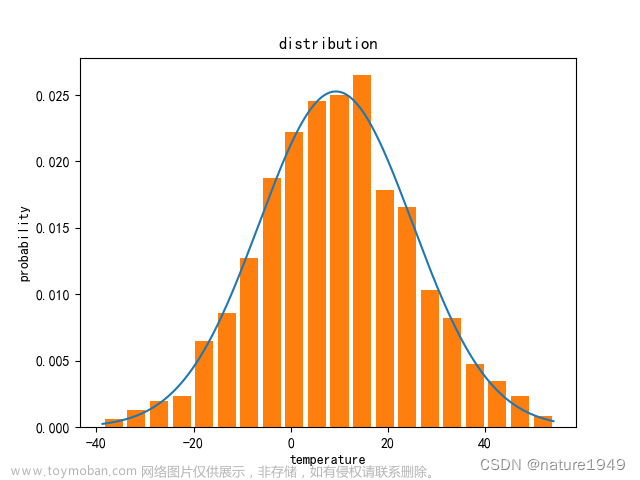
正态分布,二维正态分布,卡方分布,学生t分布——概率分布学习 python
目录 基本概念 概率密度函数(PDF: Probability Density Function) 累积分布函数(CDF: Cumulative Distribution Function) 核密度估计((kernel density estimation) 1.正态分布 概率密度函数(pdf) 正态分布累积分布函数(CDF) 正态分布核密度估计(kde) 正态分布四则运算 二维正态分布(逐渐补充) 马
-
一些常见分布-正态分布、对数正态分布、伽马分布、卡方分布、t分布、F分布等
目录 正态分布 对数正态分布 伽马分布 伽马函数 贝塔函数
-
非参数检验之符号检验、Wilcoxon符号秩检验、游程检验
目录 一、符号检验 例2.1下面是世界上71个大城市的花费指数(包括租金)按递增次序排列如下(这里上海是44位,其指数为63.5): R代码: 二、Wilcoxon符号秩检验 例2.3下面是10个欧洲城镇每人每年平均消费的酒类相当于纯酒精数(单位:升).数据已经按照升幂排列. R代码: 三、
-
非参数检验——Wilcoxon 检验 & Friedman 检验与 Nemenyi 后续检验
最近看论文,看到了Wilcoxon signed-rank test(符号秩检验),咱也不知道是个啥,就学习了一下,这里做一下笔记,方便以后查阅。 数据描述 的三个角度:集中趋势,离散程度和分布形态。 常用 统计推断检验方法 分为两大类:参数检验和非参数检验。 参数检验 通常是假设总
-
MATLAB中对方阵行列式的求解、矩阵的累加和与累乘积进行求解、矩阵的排序、矩阵的秩和迹、以及矩阵的特征值和特征向量的求解
目录 1、方阵的行列式计算 2、累加和与累乘积 (1)累加和 (2)累乘积 3、对于数据进行排序 4、求矩阵的秩 5、矩阵的迹 6、计算矩阵的特征值和特征向量 在线性代数中,对于一个方阵进行求值运算需要先将其转换为行列式,MATLAB中提供过了det函数用于对于方阵的行列式进
-
笔记检验(一):笔记检验概述
《刑事科学技术(第二版)》,主编 单大国,高等教育出版社,ISBN: 978-7-04-057361-9 (一) 笔迹的概念 笔迹是通过书写活动形成的具有个人特点的文字、符号的形象系统。笔迹具体表现为书写的字迹、符号的组合系统,它的本质是人的书写技能与书写习惯。人的书写习惯是经
-
概率统计·假设检验【正态总体均值的假设检验、正态总体方差的假设检验】
第1类错误(弃真):当原假设H 0 为真,观察值却落入拒绝域,因而拒 绝H 0 这类错误是“以真为假” 犯第一类错误的概率=显著性水平α 第2类错误(取伪):当原假设H 0 不真,而观察值却落入接受域,因而 接受H 0 以假为真 若H 0 为真,则样本值落入拒绝域{Zz α/2 }的概率是
-
SPSS参数检验、非参数检验、方差分析
在做数据分析的时候,不是只要有数据,就拿去做模型,也有很多数据,结合需求,是不需要用到模型的,比如: 奶茶店,老板想看一下,合作时间(年份为单位)与奶茶店销量的关系与差异。 像这样,只有一个自变量和一个因变量的数据,做模型效果是非常差的,也不能
-
Hosmer-Lemeshow检验(HL检验)
Hosmer-Lemeshow检验(HL检验) 为模型拟合指标,其原理在于判断预测值与真实值之间的gap情况,如果p值大于0.05,则说明通过HL检验,即说明预测值与真实值之间并无非常明显的差异。反之如果p值小于0.05,则说明没有通过HL检验,预测值与真实值之间有着明显的差异,即说明模
-
【统计】假设检验方法 一、方差齐性检验
1. 不同检验方法 最小样本量 的确认 由统计量反推得到 2. 检验方法 方差齐性检验(F检验): 两个独立样本的方差差异检验,反映了平均值的代表性。方差齐次检验前提要近似正态分布。 正态性检验: 是否符合正态分布 似然比检验: 比较样本不同似然函数,检验其分布 参
-
参数检验和非参数检验(结合SPSS分析)
概念 :是一种根据样本数据来推断总体的分布或均值、方差等总体统计参数的方法。 根据 样本 来推断 总体 的原因: 总体数据不可能全部收集到。如:质量检测问题 收集到总体全部数据要耗费大量的人力和财力 假设检验包括: 参数检验 非参数检验 基本原理 :利用小概率
-
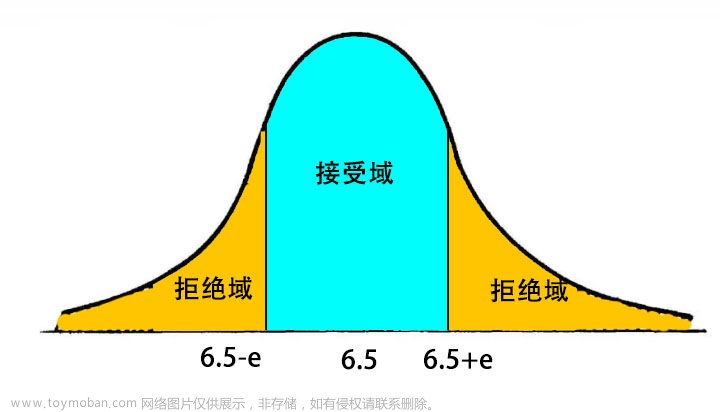
假设检验:如何理解单侧、双侧检验的拒绝域
简单说就是:拒绝域与备择假设方向相同。假设检验就是一个证伪的过程,原假设和备择假设是一对\\\"相反的结论\\\"。\\\"拒绝域\\\",顾名思义,就是拒绝原假设的范围和方向,所以判断拒绝域在哪,可以直接看备择假设H1的条件是大于还是小于即可。 上述只是判断方法之一
-
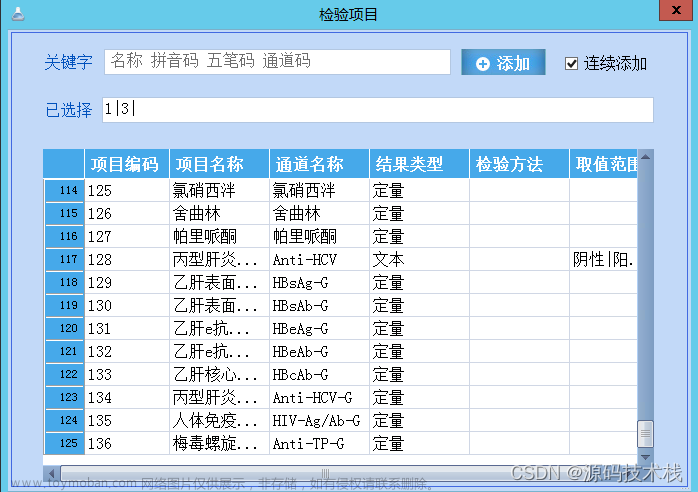
医院检验科LIS系统的常规检验项目有哪些?
白细胞数目、中性粒细胞数目、淋巴细胞数目、单核细胞数目、嗜酸性粒细胞数目、嗜碱性粒细胞数目、中性粒细胞百分比、 淋巴细胞百分比、单核细胞百分比、嗜酸性粒细胞百分比、嗜碱性粒细胞百分比、红细胞数目、血红蛋白、红细胞压积、平均红细胞体积、 平均红
-
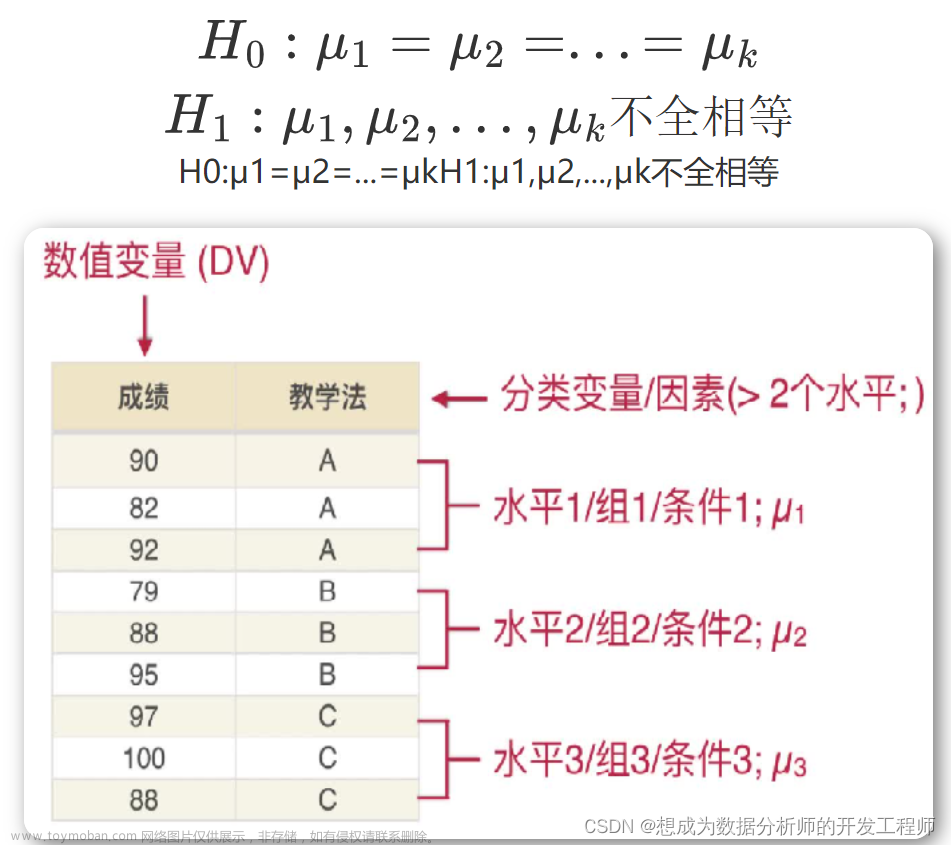
6.方差分析——单因素检验、事后检验的数学公式与代码实现
方差分析(Analysis of Variance,ANOVA)是假设检验的一种延续与扩展,主要用来对多个总体均值(三组或三组以上均值)是否相等作出假设检验,研究分类型自变量对数值型因变量的影响。 它的零假设和备择假设分别为: 方差分析的核心 因变量的总变化由两部分引起: 自变量引起