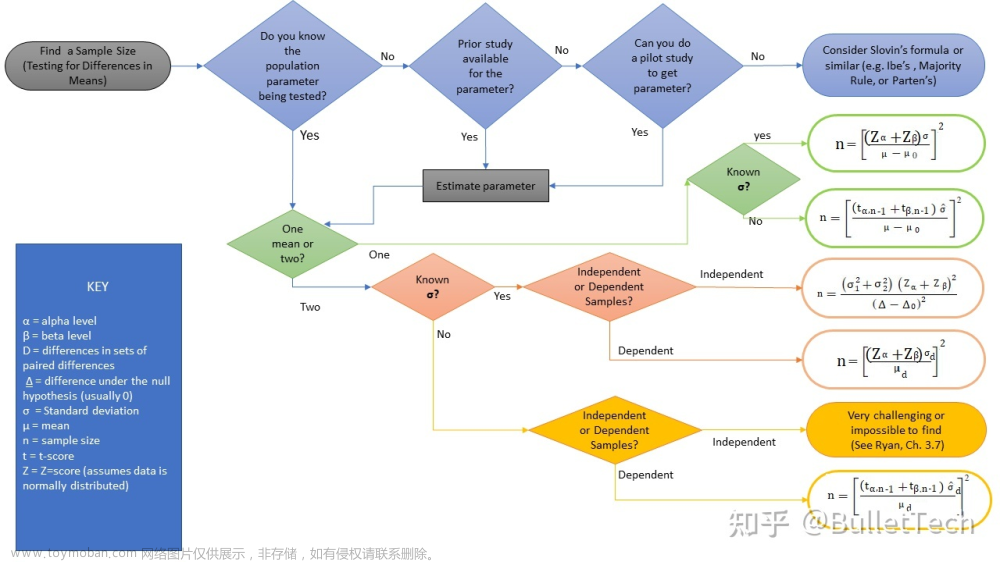
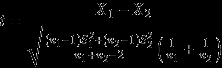秩和检验是非参数检验吗
-
【线代】矩阵的秩和线性方程组的解的情况
行最简型矩阵 :(也可以叫做行最简阶梯型矩阵,或者行简化阶梯型矩阵),其特点是:非零行的首非零元为1,且这些非零元所在的列的其它元素都为0。所谓的行最简的意思就是对应的方程组是“最简单的”,就是说,对应的方程组,最多只需要移项就行了,不再需要其他任何
-
线性代数的学习和整理18:矩阵的秩的各种定理, 秩和维度(未完成)
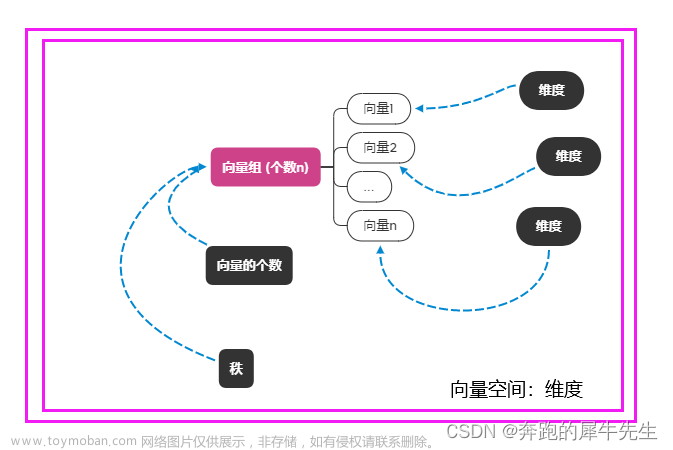
目录 0 问题引出:什么是秩? 概念备注: 1 先厘清:什么是维数? 1.1 真实世界的维度数 1.2 向量空间的维数 1.2.1 向量空间,就是一组最大线性无关的向量组/基张成的空间 1.3 向量α的维数 1.3.1 向量的维数=分量(数字/标量)个数 1.4 向量组/矩阵 A 的维数 1.4.1 什么是向量组的维
-
简述矩阵的秩和向量组的秩的定义 从定义出发分析两者之间的相互关系
(1)简述矩阵的秩和向量组的秩的定义;(2)从定义出发分析两者之间的相互关系。 (1)简述矩阵的秩和向量组的秩的定义: 矩阵的秩的定义:设在矩阵A中有一个不为0的r阶子式D,且所有的r+1阶子式(若存在)全为0,则D称为矩阵A的最高阶非零子式,它的阶数r称为矩阵
-
6.利用matlab完成 符号矩阵的秩和 符号方阵的逆矩阵和行列式 (matlab程序)
1. 简述 利用 M 文件建立矩阵 对于比较大且比较复杂的矩阵,可以为它专门建立一个 M 文件。下面通过一个简单例子来说明如何利用 M 文件创建矩阵。 例 2-2 利用 M 文件建立 MYMAT 矩阵。 (1) 启动有关编辑程序或 MATLAB 文本编辑器,并输入待建矩阵: (
-
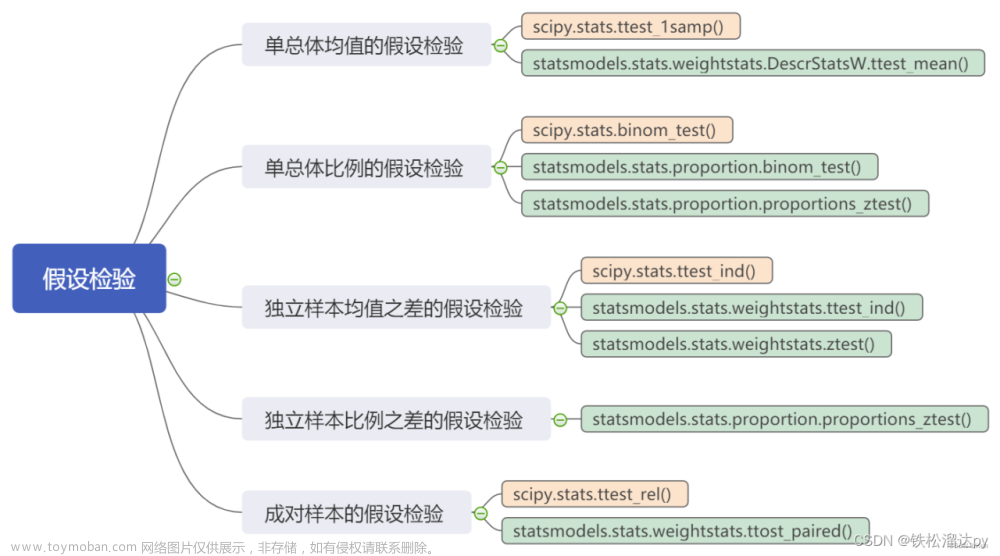
假设检验/T检验/F检验/Z检验/卡方检验
****显著性水平: 一个概率值,原假设为真时,拒绝原假设的概率,表示为 alpha 常用取值为0.01, 0.05, 0.10 ****什么是P值? p值是当原假设为真时样本观察结果及更极端结果出现的概率。 如果P值很小,说明这种情况发生的概率很小,如果这种情况还出现了,那么就有理由拒绝原
-
MATLAB中对方阵行列式的求解、矩阵的累加和与累乘积进行求解、矩阵的排序、矩阵的秩和迹、以及矩阵的特征值和特征向量的求解
目录 1、方阵的行列式计算 2、累加和与累乘积 (1)累加和 (2)累乘积 3、对于数据进行排序 4、求矩阵的秩 5、矩阵的迹 6、计算矩阵的特征值和特征向量 在线性代数中,对于一个方阵进行求值运算需要先将其转换为行列式,MATLAB中提供过了det函数用于对于方阵的行列式进
-
笔记检验(一):笔记检验概述
《刑事科学技术(第二版)》,主编 单大国,高等教育出版社,ISBN: 978-7-04-057361-9 (一) 笔迹的概念 笔迹是通过书写活动形成的具有个人特点的文字、符号的形象系统。笔迹具体表现为书写的字迹、符号的组合系统,它的本质是人的书写技能与书写习惯。人的书写习惯是经
-
概率统计·假设检验【正态总体均值的假设检验、正态总体方差的假设检验】
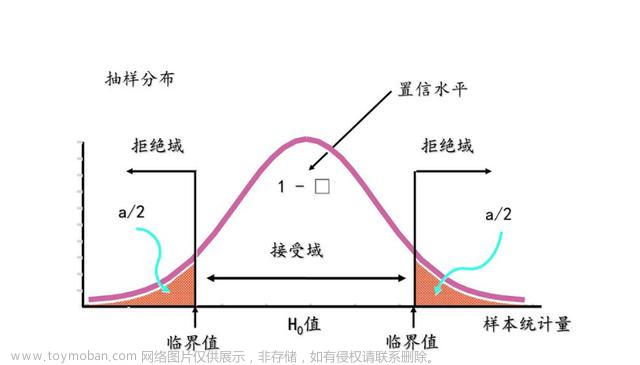
第1类错误(弃真):当原假设H 0 为真,观察值却落入拒绝域,因而拒 绝H 0 这类错误是“以真为假” 犯第一类错误的概率=显著性水平α 第2类错误(取伪):当原假设H 0 不真,而观察值却落入接受域,因而 接受H 0 以假为真 若H 0 为真,则样本值落入拒绝域{Zz α/2 }的概率是
-
T检验与Z检验的区别
概念区别: T检验 ,亦称student t检验(Student\\\'s t test),主要用于样本含量较小(例如n30),总体标准差σ未知的正态分布资料。 Z检验 是一般用于大样本(即样本容量大于30)平均值差异性检验的方法。它是用标准正态分布的理论来推断差异发生的概率,从而比较两个平均数平均
-
结合实例,直观理解正态分布、卡方分布、t分布、F分布和对应的Z检验、卡方检验、t检验、F检验
Z检验的目的是为了验证:已知一个总体服从均值,方差的正态分布,现在有一些样本,这些样本所代表的总体的均值是否为。 则构建一个统计量Z, (1) 式中,为样本均值,为总体均值,为总体方差,n为样本数量。 若零假设(null hypothesis)成立,即:样本所代表的总体的
-
Hosmer-Lemeshow检验(HL检验)
Hosmer-Lemeshow检验(HL检验) 为模型拟合指标,其原理在于判断预测值与真实值之间的gap情况,如果p值大于0.05,则说明通过HL检验,即说明预测值与真实值之间并无非常明显的差异。反之如果p值小于0.05,则说明没有通过HL检验,预测值与真实值之间有着明显的差异,即说明模
-
【统计】假设检验方法 一、方差齐性检验
1. 不同检验方法 最小样本量 的确认 由统计量反推得到 2. 检验方法 方差齐性检验(F检验): 两个独立样本的方差差异检验,反映了平均值的代表性。方差齐次检验前提要近似正态分布。 正态性检验: 是否符合正态分布 似然比检验: 比较样本不同似然函数,检验其分布 参
-
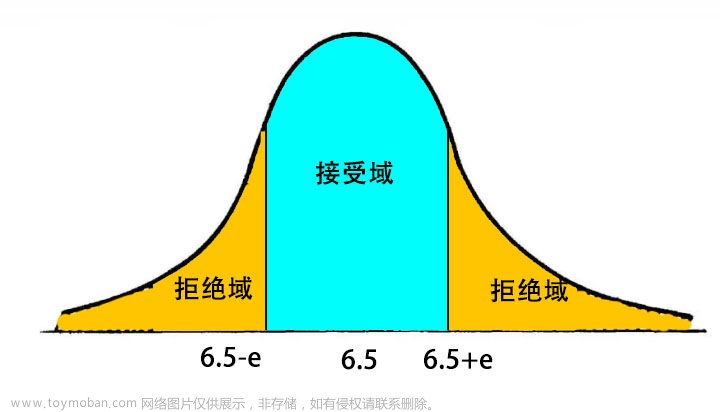
假设检验:如何理解单侧、双侧检验的拒绝域
简单说就是:拒绝域与备择假设方向相同。假设检验就是一个证伪的过程,原假设和备择假设是一对\\\"相反的结论\\\"。\\\"拒绝域\\\",顾名思义,就是拒绝原假设的范围和方向,所以判断拒绝域在哪,可以直接看备择假设H1的条件是大于还是小于即可。 上述只是判断方法之一
-
医院检验科LIS系统的常规检验项目有哪些?
白细胞数目、中性粒细胞数目、淋巴细胞数目、单核细胞数目、嗜酸性粒细胞数目、嗜碱性粒细胞数目、中性粒细胞百分比、 淋巴细胞百分比、单核细胞百分比、嗜酸性粒细胞百分比、嗜碱性粒细胞百分比、红细胞数目、血红蛋白、红细胞压积、平均红细胞体积、 平均红
-
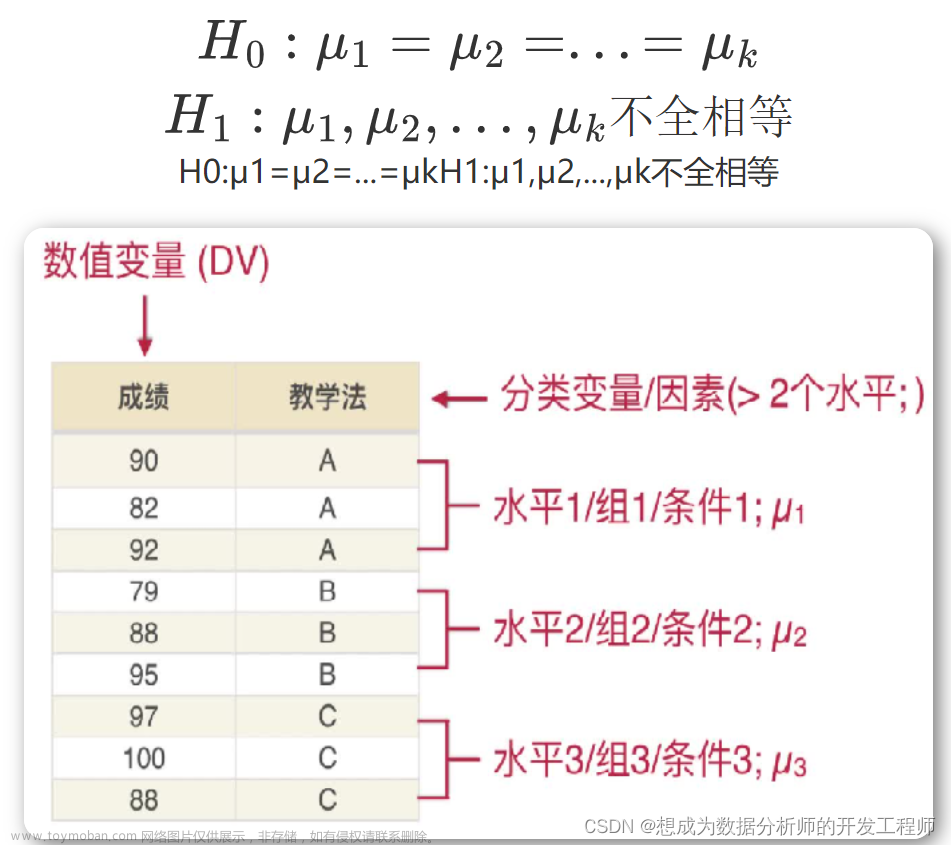
6.方差分析——单因素检验、事后检验的数学公式与代码实现
方差分析(Analysis of Variance,ANOVA)是假设检验的一种延续与扩展,主要用来对多个总体均值(三组或三组以上均值)是否相等作出假设检验,研究分类型自变量对数值型因变量的影响。 它的零假设和备择假设分别为: 方差分析的核心 因变量的总变化由两部分引起: 自变量引起
-
正态分布检验:检验序列数据是否符合正态分布
介绍 JB检验主要适用于 样本数量大于30 ,而且样本数越多,JB检验效果越准确。 JB检验主要用于 判断数据是否符合总体正态分布 ,而且构造的 JB统计量 需要符合自由度为2的卡方分布,即为 。JB统计量如下所示。 (n为样本量,S为偏度,K为峰度) JB检验主要 利用峰度 和 偏
-
显著性检验【t-test、方差分析、ks检验】
1显著性检验基本定义(what?) 2.使用显著性检验的意义(why? ) 3.显著性检验的具体操作流程(how? ) 统计假设检验(Statistical hypothesis testing) 事先对总体(随机变量)的 参数或总体分布形式做出一个假设,然后利用样本信息来判断这个假设是否合理 显著性检验(signific
-
时间序列之单位根检验+显著性检验+固定/随机效应模型选择
确定时间分隔、开始时间、结束时间 在hive中创建该表 计算每段时间内申购和赎回的量 查询每段时间开始和结束时的万份收益,计算净收益率 在面板数据和序列数据中,如果存在单位根,会产生 伪回归 等严重后果,所以必须对每个变量进行单位根检验,这样能够保证每个变
-
QMS质量检验管理|攻克制造企业质量检验难题,助力企业提质增效
在日益激烈的市场竞争中,对产品质量严格把关,是制造企业提高核心竞争力与品牌价值的关键因素。那如何高效、高质地完成产品质检工作?这就需要企业在工业质检中引进数字化技术加以辅助,进而推动智能制造高质量发展。 蓝库云QMS质量检验管理系统,涵盖来料检验、
-
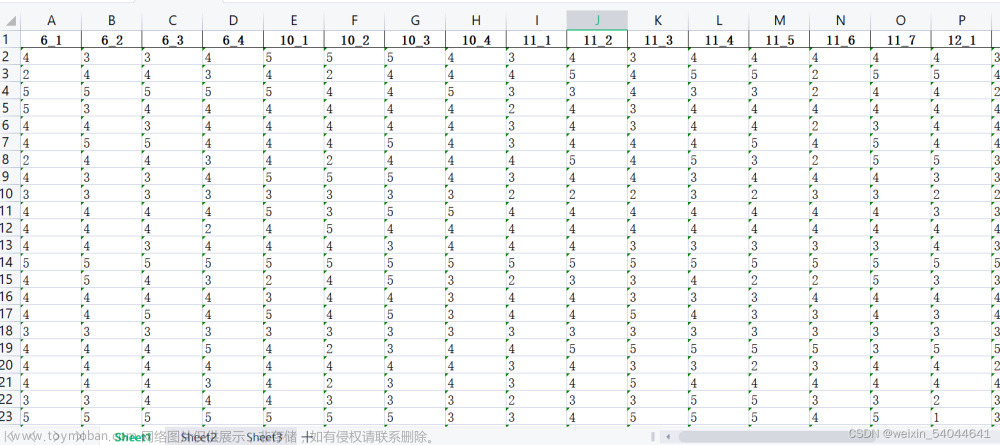
利用Python进行调查问卷的信度检验和效度检验,并对量表进行因子分析
关于问卷是否需要进行问卷信效度检验,前提时你的问卷含有量表题,量表题有两种量表:李克特量表和瑟斯顿量表 ,并且只有量表题才参与信效度检验。所以,信效度检验前需要对量表每一个选项的得分数据放到独立的一列数据中。如下图所示(Excel表) 我们说量表的信度