import numpy as np是灰色的
-
[相遇 Bug] - ImportError: numpy.core.multiarray failed to import
因为最近在看点云模型, 在自己的环境上部署该项目: https://github.com/open-mmlab/OpenPCDet/tree/master 这里执行github项目给的demo.py文件, 命令格式如下: 使用如下命令进行安装: 该解决方法是在该github项目的issue里整理得到的, 感谢里面的几位大佬! 链接及图片如下: https://github.com/open-m
-
解决opencv出错:ImportError: numpy.core.multiarray failed to import
利用安装好opencv后,导入cv2的时候报错,如下 这里是numpy库的版本过低或者过高,不合适刚刚装的opencv版本。 尝试升高或降低numpy版本,一般是升级到高版本 但也不要太高,需要兼容自己的python版本
-
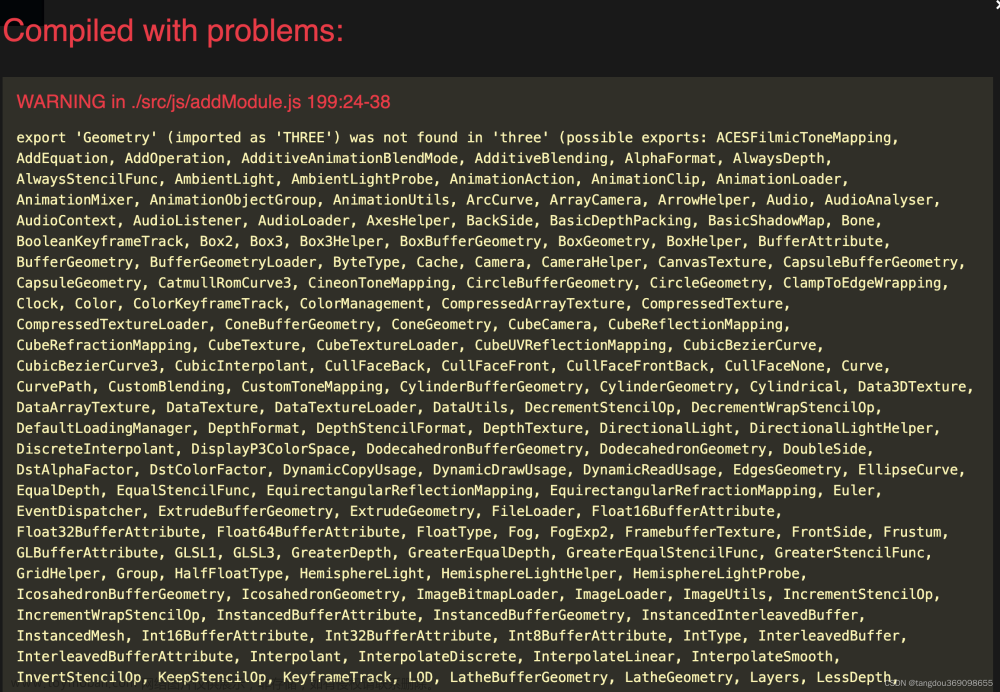
Three.js系列-报错export ‘Geometry‘ (imported as ‘THREE‘) was not found in ‘three‘
遇到这种报错,是因为你使用的是低版本的语法,需要修改为最新的,three.js 在 R125版本后将Geometry替换使用BufferGeometry 所以只需要搜索代码中的THREE.Geometry 小伙伴们,先写到这里啦,我们明天再见啦~~ 大家要天天开心哦 欢迎大家指出文章需要改正之处~ 学无止境,合作共赢 欢
-
TypeError: expected Tensor as element 0 in argument 0, but got numpy.ndarray解决办法
需要Tensor变量,我却给了numpy变量,所以转化一下就好啦!!
-
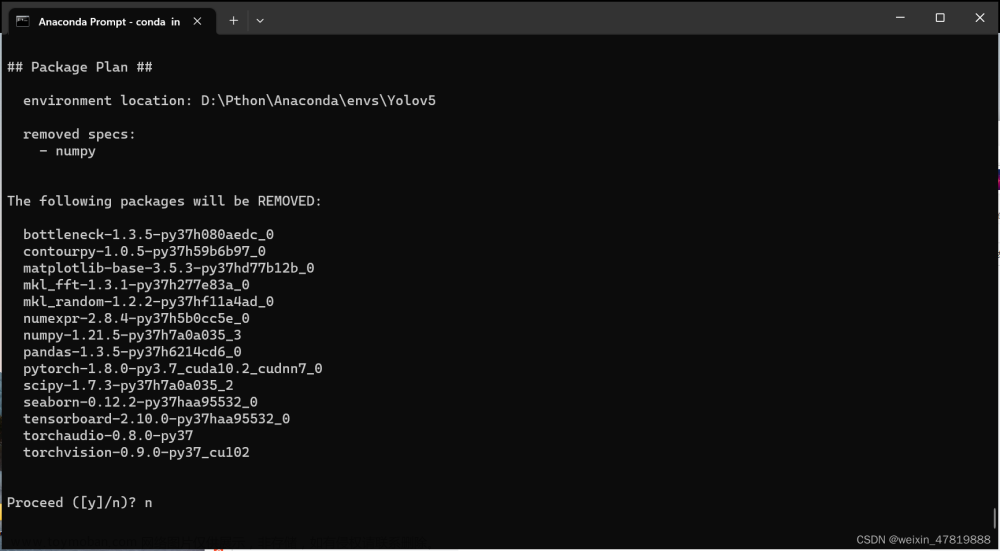
关于UserWarning: The NumPy module was reloaded (imported a second time)的解决
在用numpy时发现如下警告: 经检查后发现,base环境中安装了numpy,而新环境也安装了numpy,因而出现该问题。 处理方法 卸载base环境/新环境中的一个numpy 此处选择卸载新环境中的numpy 卸载后无警告
-
引入echars5.0报错“export ‘default‘ (imported as ‘echarts‘) was not found in ‘echarts‘解决方案
前言:老版本的echars样式与新版本的组件美观度相差巨大,以美观为主所以把组件升级成了echars5.0,结果报错了【\\\"export ‘default’ (imported as ‘echarts’) was not found in ‘echarts’】! 直接报错:\\\"export ‘default’ (imported as ‘echarts’) was not found in \\\'echarts’ 新版本的echarts引入方式
-
pycharm 运行出现UserWarning: The NumPy module was reloaded (imported a second time).
解决途中坎坷 :大家可以直接看下面的解决方案。当然我觉得大家还是先看一下我们具体所遇到的问题是否相同,避免错误解决。 看了很多博主的解决方案,还是一头污水,有的博主说是因为numpy库下载入了两次。 刚开始跟着博主说的删除numpy 库就行,结果我在
-
Traceback (most recent call last): File "D:\python项目\main.py", line 3, in <module> import pandas as pd ModuleNotFoundError
这是一个 Python 错误信息,表明在文件 \\\"D:python项目main.py\\\" 的第 3 行中尝试导入 pandas 模块时出错,错误为 \\\"ModuleNotFoundError: No module named pandas\\\"。这意味着 pandas 模块没有在你的系统上安装。要解决此问题,请使用 pip 安装 pandas:在命令行中运行 \\\"pip install pandas\\\" 即可。
-
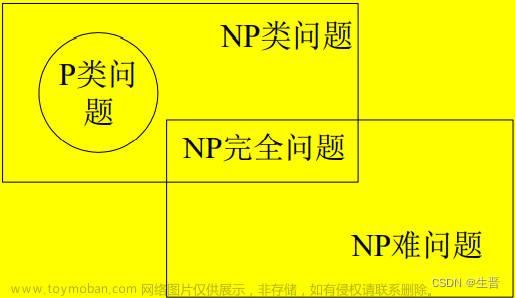
NP-Hard?大白话学习P问题、NP问题、NP完全问题和NP难问题
## 该笔记自用为主,记录一些日常学习过程中看到的不熟悉的知识和从未接触过的知识,用于回看和记录。其中有一些个人理解,如有错误请讨论指正。 在讨论这一串问题之前,我们需要复习两个概念。 1.多项式和非多项式 多项式: 非多项式:或者 2.时间复杂度 在计算机算
-
【简述】【图】P类问题、NP类问题、NP完全问题和NP难问题
1. P类问题(Polynomial Problem) P类问题 是指 一类能够用确定性算法在多项式时间内求解的判定问题 。其实,在非正式的定义中,我们可以把那些在多项式时间内求解的问题当作P类问题。 2. NP类问题(Non-deterministic Polynomial Problem) NP类问题不是非P类问
-
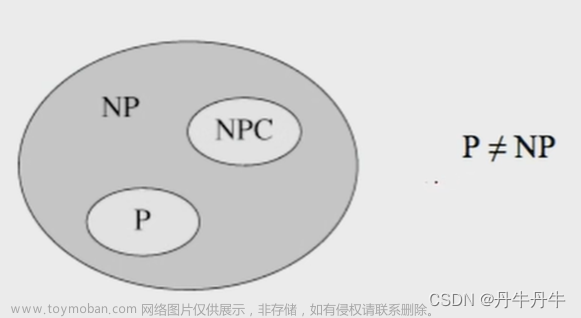
一文理解NP完全理论,NP问题,NPC问题
在以往的算法中,所接触到的大都是多项式时间内可完成的算法,比如O(n),O(nlogn),O(n^2)…,但仍存在一些算法的时间复杂度为:O(n^logn),O(2^n),O(n!)是非多项式时间算法,当此类程序规模一旦过大,便成为目前的计算机解决不了的难题。因此尝试用NP完全理论进行理解。 目录 NP问
-
【np.bincount】np.bincount()用在分割领域生成混淆矩阵
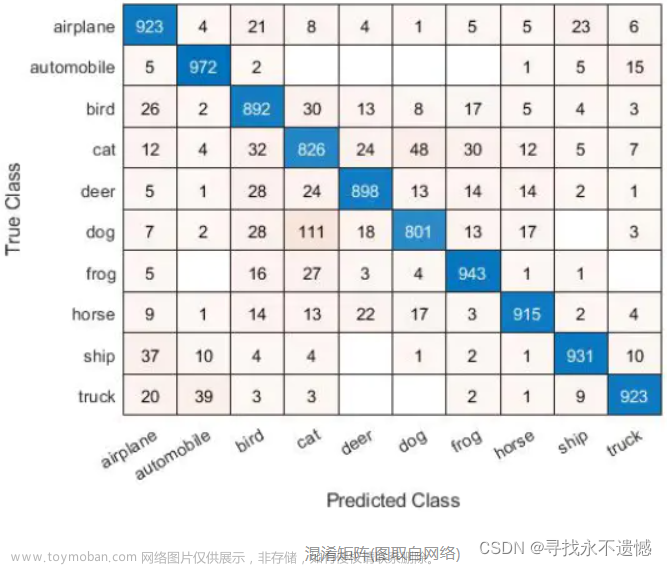
混淆矩阵:Confusion Matrix,用于直观展示每个类别的预测情况,能从中计算准确率(Accuracy)、精度(Precision)、召回率(Recall)、交并比(IoU)。 混淆矩阵是 n*n 的矩阵(n是类别),对角线上的是正确预测的数量。 每一行之和是该类的真实样本数量,每一列之和是预测为该类的样本数量
-
【Python】np.maximum()和np.minimum()函数详解和示例
本文通过函数原理和运行示例,对np.maximum()和np.minimum()函数进行详解,以帮助大家理解和使用。 更多Numpy函数详解和示例,可参考 【Python】Numpy库近50个常用函数详解和示例,可作为工具手册使用 np.maximum() 是 NumPy 库中的一个函数,用于比较两个或更多个数组元素,并返回每
-
【数学建模-灰色关联分析与灰色预测】
目录 一.灰色关联度简介 二.灰色关联度 灰色关联分析案例 三.灰色预测模型简介 四.灰色预测之灰色生成数列 累加生成 累减生成 加权邻值生成 五.灰色模型GM(1,1) GM(1,1)灰色预测的步骤 1.数据的检验与处理 2.建立GM(1,1)模型 3. 检验预测值 六.灰色预测案例 灰色
-
np.bincount方法
官方文档 out = np.bincount(x[, weights, minlength]) 该函数用于统计输入数组内每个数值出现的次数,输出数组中的索引值对应的是输入数组中的元素值,若输入数组中的某个数值出现了一次,则输出数组对应索引值上的数加一 x: 输入,1维非负数组 weights: 权重数组, 可选参数,如果指
-
np.concatenate函数
np.concatenate((a1, a2, …), axis=0) concatenate函数沿着某axis轴将a1、a2等数组进行合并。 总是记不住axis对应的方向,看到官网的examples觉得很容易懂,记录一下。 其中axis(读着aeksis,记住这里的x发音ks就可以)为0和1时分别代表不同的拼接方向。 当axis为0时,数组沿着横轴拼接,这
-
np.random.randint
np.random.randint 是 Numpy 库中的一个函数,用于生成随机整数。该函数的用法如下: np.random.randint(low, high=None, size=None, dtype=\\\'l\\\') 其中: low:生成的随机整数的下限(包含) high:生成的随机整数的上限(不包含) size:生成数组的形状 dtype:生成数组的数据类型 例如,以下代码生成一
-
np.argmin()函数
各个参数意义: a :输入数组。 axis :可选参数,默认的是去展平数组,此外就是沿着特定的方向。 out :可选参数,如果被提供,那么结果就会被插入到这个数组中,注意该数组一定要有合适的形状和数据类型。 keepdims :可选参数, True 或者 False 。如果 keepdims 设置为 Fal
-
np.random.normal
np.random.normal函数是numpy库中用于生成正态分布(也叫高斯分布)随机数的函数。 normal------正态 np.random.normal(loc=0.0, scale=1.0, size=None) 该函数有三个参数:loc, scale, size loc表示随机数的期望值(对应着整个分布的中心)。float ,loc=0说明这一个以Y轴为对称轴的正态分布 scale表示随机数
-
什么是P = NP?问题
提示:以下是本篇文章正文内容,Java系列学习将会持续更新 今天我们先放松一下,这篇文章并不是Java课程的学习,而是带大家认识一个学术问题。但是请大家放心,这里并 不是学术的探讨 ,因为我也不懂,我只是搜集一些相关的资料带大家了解一下这个问题。更多的是

![[相遇 Bug] - ImportError: numpy.core.multiarray failed to import](https://imgs.yssmx.com/Uploads/2024/02/576301-1.png)