背包问题

通过详细解析背包问题的动态规划解法，包括状态设计、状态转移方程、两种编码方法（自顶向下和自下而上），以及滚动数组的优化，帮助理解和实现动态规划算法。

目录 前言背包问题的历史  01背包  1、题目 2、暴力解01背包  Ⅰ、代码 3、动态规划解01背包 Ⅰ、二维dp数组解01背包 1）dp数组的含义  2）递推公式  3）dp数组的初始化  4）遍历顺序的讨论  5、代码  Ⅱ、一维数组解01背包  1）一维数组|滚动数组  2）一维数组的含义及递

题目描述 有n件物品和一个最大承重为w 的背包。第i件物品的重量是weight[i]，每件只能用一次，求装入背包的最多物品数量。 题目分析 因为我们 只要求装入物品的数量 ，所以 装重的显然没有装轻的划算 。 因此将 数组weight[i]按从小到大排序 ， 依次选择每个物品 ，直到装不

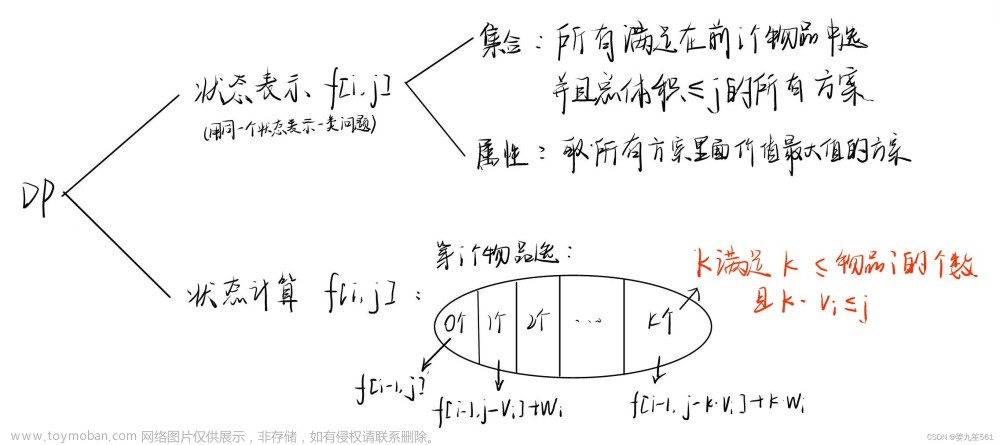
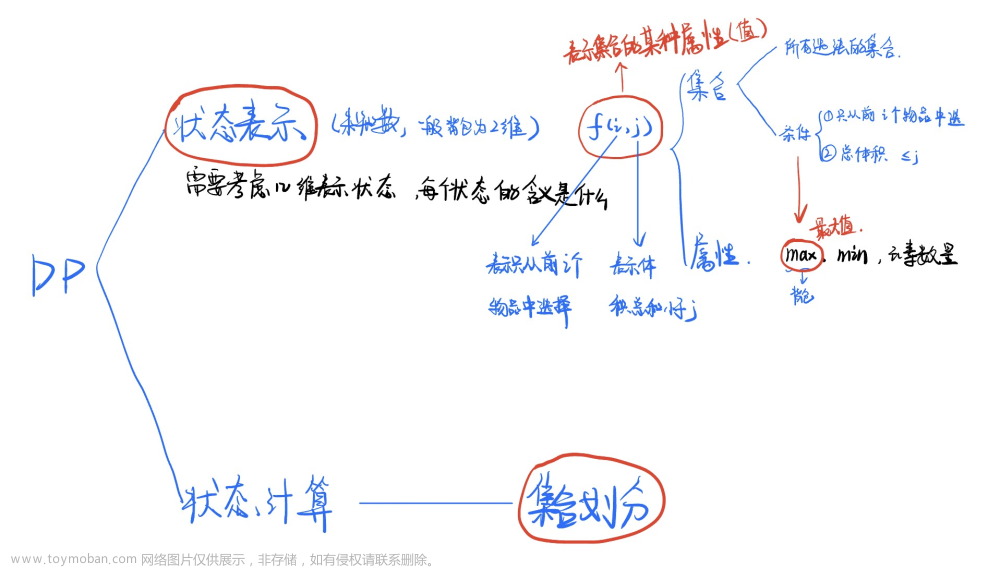
一、01背包问题 问题描述： 有 N 件物品和一个容量为 V 的背包，每件物品有各自的价值且只能被选择一次，要求在有限的背包容量下，装入的物品总价值最大。 朴素01背包 状态f[i , j]定义：在前i个物品中选，总体积不超过j的价值最大值 状态转移 1） 选第i个物品：f[i,j] = f

目录 DP分析： 优化：  二进制优化 例题：         01背包是每个物品只有一个，完全背包问题是每个物品有无限个。         那么多重背包问题就是 每个物品有有限个 。 有 N 种物品和一个容量是 V 的背包。 第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。 求解

0 1 背包问题： 条件：N 个物品容量为 V 的背包，每件物品最多用 1 次，其中物品信息体积为 Vi，价值为 Wi。 目标：选出物品，使价值最大（不一定装满背包）。 特点：每件物品 最多只用 1 次 完全背包问题： 特点：每一件物品都有 无限个 多重背包问题： 特点：每个物品

对比01背包，完全背包中的每件物品有无数件。 也就是说，每件物品可以拿0，1，…，k，…件。 dp[i][j]表示前i种物品，体积为j时的最大价值 对于第i件物品： 不拿：dp[i][j]⇐dp[i-1][j] 拿一件：dp[i][j]⇐dp[i-1][j-w[i]]+v[i] 拿两件：dp[i][j]⇐dp[i-1][j-2w[i]]+2v[i] … 拿k件：dp[i]][j]⇐dp[i

算法相关数据结构总结： 序号 数据结构 文章 1 动态规划 动态规划之背包问题——01背包 动态规划之背包问题——完全背包 动态规划之打家劫舍系列问题 动态规划之股票买卖系列问题 动态规划之子序列问题 算法（Java）——动态规划 2 数组 算法分析之数组问题 3 链表 算法

完全背包问题： 每个物品使用次数没有限制，与0-1背包的不同之处在于 遍历背包的顺序 是正序。 多重背包问题： 与完全背包的区别在于，每一种物品是有个数限制的，不能无限选择。这篇博客讲解的非常详细，可以参考学习： 多重背包问题---超详细讲解+优化（不懂你揍我

目录 什么是背包问题？ 动态规划问题的一般解决办法： 0-1背包问题： 0 - 1背包类问题  分割等和子集：  完全背包问题：  完全背包类问题 零钱兑换II: 背包问题(Knapsack problem)是一种组合优化的NP完全问题。 问题可以描述为：给定一组物品，每种物品都有自己的重量和价格

⭐️ 前面的话 ⭐️ 本篇文章将介绍动态规划中的背包问题——完全背包问题，前面我们已经介绍了0-1背包问题，其实完全背包问题就只改了0-1背包问题的一个条件，即物品可选择次数由一次改为无数次，仅此而已，下面我们就来开始介绍完全背包问题。 📒博客主页：未见

【题目描述】 设有n�种物品，每种物品有一个重量及一个价值。但每种物品的数量是无限的，同时有一个背包，最大载重量为M�，今从n�种物品中选取若干件(同一种物品可以多次选取)，使其重量的和小于等于M�，而价值的和为最大。 【输入】 第一行:两个整数，M�(背包

有5件物品和1个背包，背包最多只能装下8公斤的物品。怎样选择物品，使得背包能装下并且得到的价值最大。物品的重量和价值如下所示： 物品1: 6公斤    价值48元 物品2: 1公斤   价值7元 物品3: 5公斤   价值40元 物品4: 2公斤    价值12元 物品5: 1公斤   价值8元 可以先考虑

01 背包 概念：有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是 w e i g h t [ i ] weight[i] w e i g h t [ i ] ，得到的价值是 v a l u e [ i ] value[i] v a l u e [ i ] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。 方法1：暴力回溯法 方法2：动态规划 三个

本文旨在加强01背包问题的记忆与理解，步骤会细化 小明有一个容量为 VV的背包。 这天他去商场购物，商场一共有 N 件物品，第 i 件物品的体积为 w ，价值为 v 。 小明想知道在购买的物品总体积不超过 V 的情况下所能获得的最大价值为多少，请你帮他算算。 输入描述 输入第