-
什么是恶意代码分析中的动态分析基础技术?
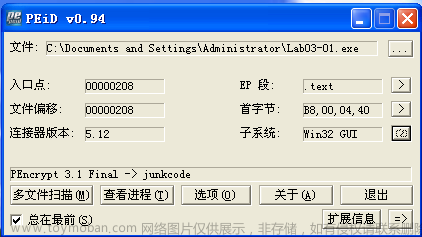
你知道如何使用动态分析基础技术来分析Lab03-01.exe文件中的恶意代码吗?Lab03-02.dll中的恶意代码如何自行安装?Lab03-03.exe的恶意代码在主机上的感染迹象是什么?Lab03-04.exe的恶意代码运行时会发生什么?动态分析为何无法有效实施?
-
什么是恶意代码分析中的动态分析基础技术?
你知道如何使用动态分析基础技术来分析Lab03-01.exe文件中的恶意代码吗?Lab03-02.dll中的恶意代码如何自行安装?Lab03-03.exe的恶意代码在主机上的感染迹象是什么?Lab03-04.exe的恶意代码运行时会发生什么?动态分析为何无法有效实施?
-
算法分析与设计--动态规划
一、动态规划简介 二、动态规划求解步骤 三、动态规划典型应用 数字三角形问题 最大子段和问题 0-1背包问题 四、最长公共子序列问题 动态规划求解 五、总结 算法语言--java语言 动态规划算法通常用于求解具有某种最优性质的问题。动态规划与分治算法类似,其基本思想也
-
算法分析03--动态规划
4.1.1 动态规划的基本思路 动态规划算法与分治法类似, 其基本思想也是将待求解问题分解成若干个子问题, 先求解子问题, 然后从这些子问题的解得到原问题的解。 与分治法不同的是,适合用动态规划法求解的问题,经分解得到的子问题往往不是独立的。若用分治法来解
-
动态代理AOP机制分析
有一个接口Vehicle,接口里有个run方法,有一个汽车类和一个轮船类,实现了这个接口。 要求在运行Car对象的run方法或运行ship对象的run方法前输出一些日志。 交通工具开始运行了… 轮船在海上running 交通工具停止运行了… 交通工具开始运行了… 轮船在海上running 交通工具停
-
【算法分析与设计】动态规划(上)
理解动态规划算法的概念 。 掌握动态规划算法的基本要素 : (1) 最优子结构性质 (2) 重叠子问题性质 掌握设计动 态规划算法的步骤 : (1) 找出最优解的性质,并刻划其结构特征 。 (2) 递归地定义最优值 。 (3) 以自底向上的方式计算
-
算法设计与分析复习--动态规划
算法设计与分析复习–递归与分治(二) 与分析法类似:将原问题分解为子问题 不同点:不是通过递归的方式,而是自底向上的求解问题 矩阵连乘的次数是左矩阵行列,右矩阵行列取出左右中进行相乘。 由于矩阵乘积需要满足左矩阵列等于右矩阵的行,所以可以用一维数组
-
算法设计与分析—动态规划例题
题目描述 求FIB数列第n项的值 输入 输入一个整数n,表示需要输出FIB数列第n项的值 输出 输出FIB数列第n项的值 样例输入 复制 样例输出 复制 提示 题目描述 长江游艇俱乐部在长江上设置了n (n=10)个游艇出租站1,2,…,n。游客可在这些游艇出租站租用游艇,并在下游的
-
算法分析与设计---分治+动态规划
1.分治法 适用条件: 问题规模缩小到一定程度容易求解 问题可以分解为若干个规模较小的 相同 子问题,即问题具有最优子结构( 使用分治法前提 ) 可以利用子问题的解合并为该问题的解( 决定是否使用分治法 ) 各个子问题 相互独立 ,即子问题之间不包含公共子问题(
-
算法设计与分析实验---动态规划
任务描述 沿着河岸摆放 N 堆石子,现要将石子有次序地合并成一堆,规定每次只能选相邻的 2 堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。 例如: 4 堆石子 4,5,9,4 ,可以按 (((4,5),9),4) 合并。 第一次合并得分是 9 分,合并之后石子堆是 9,9,4 第二次合并得
-
【算法分析与设计】动态规划(下)
若给定序列X={x1,x2,…,xm},则另一序列Z={z1,z2,…,zk},是X的 子序列 是指 存在一个严格递增下标序列{i1,i2,…,ik}使得对于所有j=1,2,…,k有:zj=xij 。例如,序列Z={B,C,D,B}是序列X={A,B,C,B,D,A,B}的子序列,相应的递增下标序列为{2,3,5,7}。 给定2个序列X和Y,当另
-
【算法设计与分析】作业2:动态规划
最长递增⼦序列(LIS) 编程实现求解最长递增⼦序列的三种动态规划算法(⼀些细节请参考课件) 1.1 算法1:令 L ( k ) L(k) L ( k ) 表示 s [ 1.. n ] s[1..n] s [ 1.. n ] 中以 s [ k ] s[k] s [ k ] 结尾的LIS的长度,原问题即求解 max 1 ≤ k ≤ n L ( k ) max_{1le kle n}L(k) max 1 ≤ k ≤ n L ( k
-
算法设计与分析 实验三 动态规划
1.打家劫舍: 给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。 入: 每组测试案例有两行,第一行只有一个整数N,代表着有N间房屋 第二行有N个整数,代表着每间房屋里的金额,金额范围[0, 1000]。 出:
-
3.2 多级放大电路的动态分析
一个 N N N 级放大电路的交流等效电路可用图3.2.1所示方框图表示。由图可知,放大电路中前级的输出电压就是后级的输入电压,即 U ˙ o 1 = U ˙ i 2 dot U_{o1}=dot U_{i2} U ˙ o 1 = U ˙ i 2 、 U ˙ o 2 = U ˙ i 3 dot U_{o2}=dot U_{i3} U ˙ o 2 = U ˙ i 3 、 ⋯ cdots ⋯ 、 U ˙ o ( N − 1
-
供水管网动态模型分类及应用分析
当供水管网中发生启停泵、快速关阀等事件时, 延时时段模拟 (即准稳态模型) 不能准确预测系统的瞬时动态变化, 而需要采用更为准确复杂的瞬变流动态模型。为明确多种动态模型之间的差异, 探讨和分析了供水管网动态模型的分类、模型理论以及在管网运行管理中的