PDF.js CORS 问题
我从域 A 将 PDF.js 加载到 iframe 中,并以文件作为参数(服务器的完整路径,这将返回 pdf 文档)。PDF.js 将向域 B 的服务器创建一个请求,扩展名为origin: domain A. 域 B 的服务器返回带有 header 的 pdf 文档Access-Control-Allow-Origin: domain A,到目前为止一切顺利。 在我的网络选项卡中,
如何解决Mysql无法使用root用户登录问题
最近 Vagrant+ Oracle VM VirtualBox 在本地环境配置Linux开发环境, 发现通过宝塔面板安装Mysql 数据库 之后 用Navicat 远程连接 登录 root 登录不了。
Driver [Think] not supported.
使用 Thinkphp6.0 模板渲染的时候报错Driver [Think] not supported. 因为没有安装 模板引擎think-view composerrequiretopthink/think-view
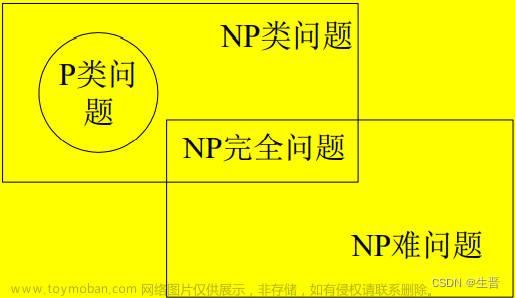
【简述】【图】P类问题、NP类问题、NP完全问题和NP难问题
1. P类问题(Polynomial Problem) P类问题 是指 一类能够用确定性算法在多项式时间内求解的判定问题 。其实,在非正式的定义中,我们可以把那些在多项式时间内求解的问题当作P类问题。 2. NP类问题(Non-deterministic Polynomial Problem) NP类问题不是非P类问
记录pip问题(解决下载慢的问题、升级失败问题)
目录 一、解决下载慢的问题 1、问题分析 2、解决办法 (1)下载时加入参数 -i [镜像源地址] 例如: (2)使用命令——设置源(推荐) (3)修改配置文件——设置源(推荐) pip国内镜像源汇总 二、pip升级失败问题 1、前言 2、解决方法 三、对于pip问题一劳永逸解决方案
详解经典进程同步问题(生产者消费者问题/哲学家进餐问题/读者写者问题)_OS
目录 1. 利用信号量实现进程的同步和互斥 利用信号量实现进程互斥 利用信号量实现进程同步 2. 生产者消费者问题 3. 哲学家就餐问题 4. 读者写者问题 读者优先 写者优先 读者写者问题的变形 使用信号量解决读者写者问题 5. 经典同步问题例题 6. 管程机制 使用管程解决生产者
NP-Hard?大白话学习P问题、NP问题、NP完全问题和NP难问题
## 该笔记自用为主,记录一些日常学习过程中看到的不熟悉的知识和从未接触过的知识,用于回看和记录。其中有一些个人理解,如有错误请讨论指正。 在讨论这一串问题之前,我们需要复习两个概念。 1.多项式和非多项式 多项式: 非多项式:或者 2.时间复杂度 在计算机算
[问题处理] 简化问题复现步骤
当一个问题在复杂的场景下发生之后,在做调试的时候,总是希望可以将复现的步骤简化,以方便问题debug。这里总结一下一般实例。 当在大量业务数据流做压力测试时,发现TCP有丢包;可能需要使用网络相关的性能测试软件来简化复现步骤,将复杂的业务去掉; 当一个复杂
问题: 视频颜色问题,偏绿
什么是杜比视界? - https://www.youtube.com/watch?v=ldXDQ6VlC7g 【哈士亓说】07:HDR、杜比视界究竟是个啥?为什么这个视频还不是HDR视频? - https://www.youtube.com/watch?v=rgb9Xg3cJns 视频应该是 杜比视界 电影 颜色应该是 偏红绿色 [中文名] 名称 [年份] [剪辑版本] [发布说明] 分辨率 来源 [音
动态规划问题实验:数塔问题
动态规划是一种解决复杂问题的方法,它将一个问题分解为若干个子问题,然后从最简单的子问题开始求解,逐步推导出更复杂的子问题的解,最终得到原问题的最优解。动态规划的关键是找到子问题之间的递推关系,以及确定合适的边界条件和初始值。 数塔问题是一个经典
【大厂面试问题】:飞机绕行地球问题
目录 目录 你的阅读是我最大的动力编辑 问题描述: 引出思路: 一台加油飞机 两台加油飞机 返航方案一:加油机I、II同时起飞。 返航方案二:加油机I先起飞加油机II再起飞(加油机II与加油机I差2个身位才起飞) 返航方案三:加油机I先起飞加油机II再起飞(加油机II与加油机
dockerfile传参问题和权限问题
在工作中,使用dockerfile构建镜像的时候,随着业务越来越多,流水线也越来越多,这时候就需要构建一些通用流水线,而通用流水线最大的问题,就是需要传递参数,通过传递不同的参数去构建不同的服务 1、–build-arg 这个参数可以让你在docker build的时候,指定需要传递的参
小程序缓存问题,h5缓存问题
通过打包的时候加了配置 会自动将静态资源文件后面追加hash数值,这样静态文件发生变化的时候会生成新的hash值,之后每次发包的静态文件路径就是不同的了,所以升级版本就避免了缓存的问题 是小程序跳转h5 时候参数带有时间戳,每次打开都是新的链接 3.通过meta标签清
斐波那契问题——上台阶问题
题目: 给定整数N,代表台阶数,一次可以跨2个或者1个台阶,返回有多少种走法。 举例: N=3,可以三次跨一个台阶,也可以先跨2再跨1,也可以先跨1再跨2,共三种走法。 思路: 如果台阶只有1级,方法只有一种,如果台阶有两级,方法有两种。如果台阶有N级,最后跳上



![Driver [Think] not supported.](https://www.toymoban.com/Uploads/news/33.jpg)





![[问题记录] oracle问题汇总记录](https://imgs.yssmx.com/Uploads/2024/04/844700-1.png)

