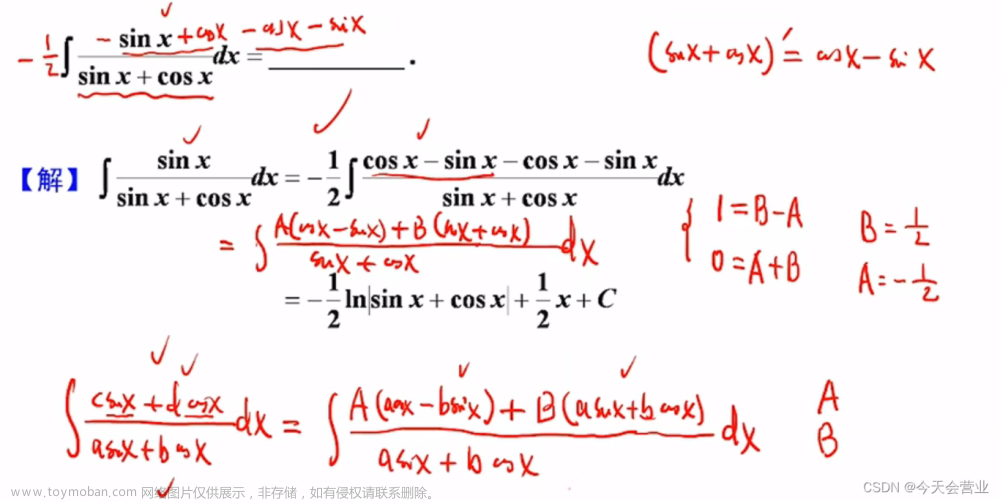定积分与不定积分的差别
根据牛顿-莱布尼茨公式,许多函数的定积分的计算就可以简便地通过求不定积分来进行。这里要注意不定积分与定积分之间的关系:定积分是一个数,而不定积分是一个表达式,它们仅仅是数学上有一个计算关系。一个函数,可以存在不定积分,而不存在定积分,也可以存在定积分,而没有不定积分。连续函数,一定存在定积分和不定积分;若在有限区间[a,b]上只有有限个间断点且函数有界,则定积分存在;若有跳跃、可去、无穷间断点,则原函数一定不存在,即不定积分一定不存在。
不定积分的定义与计算
不定积分的定义
∫ f ( x ) d x = F ( x ) + C \int f_{(x)}dx = F_{(x)} + C ∫f(x)dx=F(x)+C设F(x)是函数f(x)的一个原函数,我们把函数 f ( x ) f(x) f(x)的所有原函数 F ( x ) + C F(x)+ C F(x)+C(其中,C为任意常数)叫做函数 f ( x ) f(x) f(x)的不定积分,又叫做函数 f ( x ) f(x) f(x)的反导数,记作 ∫ f ( x ) d x 或者 ∫ f ( x ) ∫f(x)dx或者∫f(x) ∫f(x)dx或者∫f(x)(高等微积分中常省去dx),即 ∫ f ( x ) d x = F ( x ) + C ∫f(x)dx=F(x)+C ∫f(x)dx=F(x)+C。其中 ∫ ∫ ∫叫做积分号, f ( x ) f(x) f(x)叫做被积函数, x x x叫做积分变量, f ( x ) d x f(x)dx f(x)dx叫做被积式, C C C叫做积分常数或积分常量,求已知函数的不定积分的过程叫做对这个函数进行不定积分。
不定积分的计算
函数的和的不定积分等于各个函数的不定积分的和;即:设函数 f ( x ) f(x) f(x)及 g ( x ) g(x) g(x)的原函数存在,则

求不定积分时,被积函数中的常数因子可以提到积分号外面来。即:设函数 f ( x ) f(x) f(x)的原函数存在, k k k非零常数,则

定积分的定义
设函数
f
(
x
)
f(x)
f(x) 在区间
[
a
,
b
]
[a,b]
[a,b]上连续,将区间
[
a
,
b
]
[a,b]
[a,b]分成n个子区间
[
x
0
,
x
1
]
,
(
x
1
,
x
2
]
,
(
x
2
,
x
3
]
,
…
,
(
x
n
−
1
,
x
n
]
[x0,x1], (x1,x2], (x2,x3], …, (xn-1,xn]
[x0,x1],(x1,x2],(x2,x3],…,(xn−1,xn],其中
x
0
=
a
,
x
n
=
b
x0=a,xn=b
x0=a,xn=b。可知各区间的长度依次是:
△
x
1
=
x
1
−
x
0
△x1=x1-x0
△x1=x1−x0,在每个子区间
(
x
i
−
1
,
x
i
]
(xi-1,xi]
(xi−1,xi]中任取一点
ξ
i
(
1
,
2
,
.
.
.
,
n
)
ξi(1,2,...,n)
ξi(1,2,...,n),作和式。该和式叫做积分和,设
λ
=
m
a
x
△
x
1
,
△
x
2
,
…
,
△
x
n
λ=max{△x1, △x2, …, △xn}
λ=max△x1,△x2,…,△xn(即λ是最大的区间长度),如果当
λ
→
0
λ→0
λ→0时,积分和的极限存在,则这个极限叫做函数
f
(
x
)
f(x)
f(x) 在区间
[
a
,
b
]
[a,b]
[a,b]的定积分,记为,并称函数
f
(
x
)
f(x)
f(x)在区间
[
a
,
b
]
[a,b]
[a,b]上可积。 其中:
a
a
a叫做积分下限,
b
b
b叫做积分上限,区间
[
a
,
b
]
[a, b]
[a,b]叫做积分区间,函数
f
(
x
)
f(x)
f(x)叫做被积函数,
x
x
x叫做积分变量,
f
(
x
)
d
x
f(x)dx
f(x)dx 叫做被积表达式,$∫ $叫做积分号。
之所以称其为定积分,是因为它积分后得出的值是确定的,是一个常数, 而不是一个函数。
定积分的计算
-
当a=b时, ∫ a b f ( x ) d x = 0 \int_a^b f(x)dx = 0 ∫abf(x)dx=0
-
当a>b时, ∫ a b f ( x ) d x = − ∫ a b f ( x ) d x \int_a^b f(x)dx = -\int_a^bf(x)dx ∫abf(x)dx=−∫abf(x)dx
-
常数可以提到积分号前。

-
代数和的积分等于积分的代数和。

-
定积分的可加性:如果积分区间[a,b]被c分为两个子区间[a,c]与[c,b]则有

-
若f(x)在区间D上可积,区间D中任意c(可以不在区间[a,b]上)满足条件。
如果在区间[a,b]上,f(x)≥0,则
-
积分中值定理:设f(x)在[a,b]上连续,则至少存在一点ε在[a,b]内使

常见的积分公式如下:
以下的C都是指任意积分常数:文章来源:https://www.toymoban.com/news/detail-400328.html
∫
a
d
x
=
a
x
+
C
\int adx=ax+C
∫adx=ax+C,a是常数
∫
x
a
d
x
=
x
a
+
1
a
+
1
+
C
\int x^adx = \frac{x^{a+1}}{a+1}+C
∫xadx=a+1xa+1+C,其中a为常数,且a
≠
\neq
=-1
∫
1
x
d
x
=
l
n
∣
x
∣
+
C
\int \frac{1}{x}dx = ln|x| +C
∫x1dx=ln∣x∣+C
∫
e
x
d
x
=
e
x
+
C
\int e^xdx = e^x+C
∫exdx=ex+C
∫
a
x
d
x
=
1
l
n
a
a
x
+
C
\int a^xdx=\frac{1}{lna}a^x+C
∫axdx=lna1ax+C,其中a>0,且a
≠
\neq
= 1
∫
s
i
n
x
d
x
=
−
c
o
s
x
+
C
\int sinxdx = -cosx+C
∫sinxdx=−cosx+C
∫
c
o
s
x
d
x
=
s
i
n
x
+
C
\int cosxdx = sinx+C
∫cosxdx=sinx+C
∫
s
e
c
2
x
d
x
−
t
a
n
x
+
C
\int sec^2xdx - tanx+C
∫sec2xdx−tanx+C
∫
c
s
c
2
x
d
x
=
−
c
o
t
x
+
C
\int csc^2xdx = -cotx+C
∫csc2xdx=−cotx+C
∫
t
a
n
x
d
x
=
−
l
n
∣
c
o
s
x
∣
+
C
\int tanxdx = -ln|cosx|+C
∫tanxdx=−ln∣cosx∣+C
∫
c
o
t
x
d
x
=
l
n
∣
s
i
n
x
∣
+
C
\int cotxdx = ln|sinx|+C
∫cotxdx=ln∣sinx∣+C
∫
s
e
c
x
d
x
=
l
n
∣
s
e
c
x
+
t
a
n
x
∣
+
C
\int secxdx = ln|secx+tanx|+C
∫secxdx=ln∣secx+tanx∣+C
∫
c
s
c
x
d
x
=
l
n
∣
c
s
c
x
−
c
o
t
x
∣
+
C
\int cscxdx = ln|cscx-cotx|+C
∫cscxdx=ln∣cscx−cotx∣+C文章来源地址https://www.toymoban.com/news/detail-400328.html
到了这里,关于不定积分与定积分(高等数学)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!