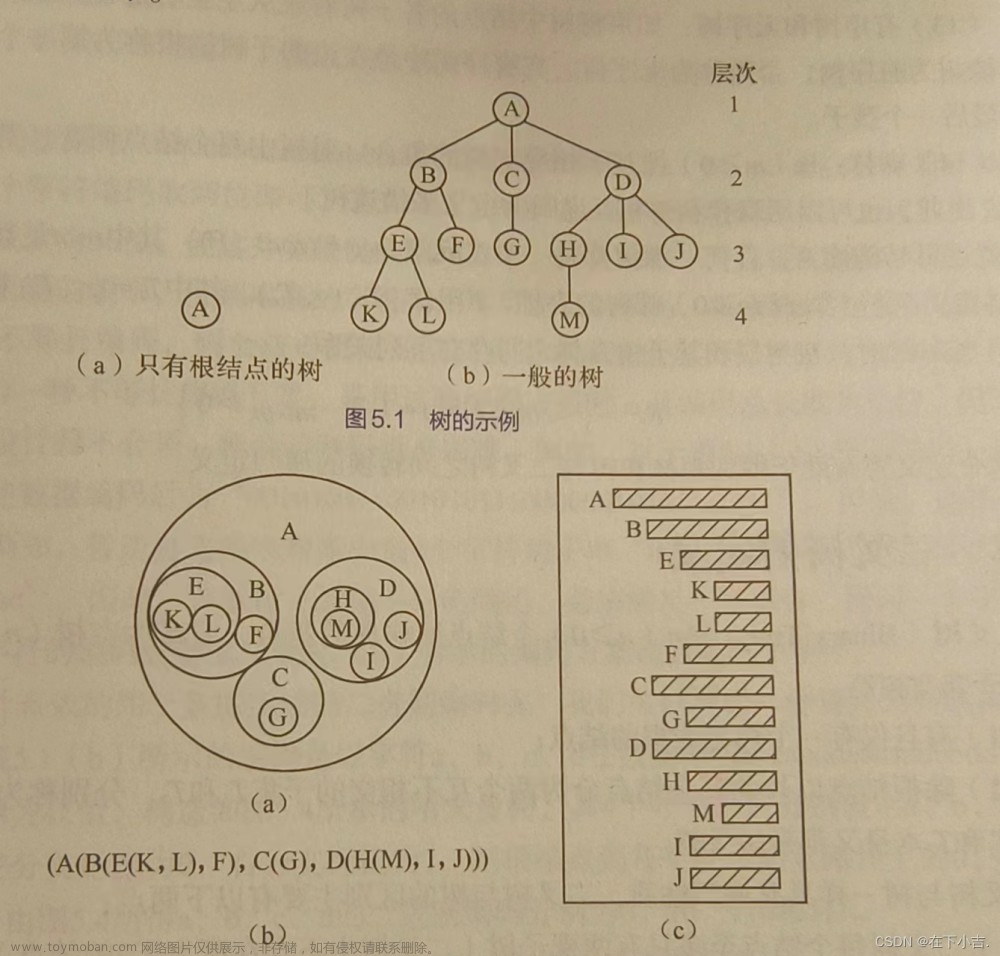
【二叉树】大学有棵树叫高数,数据结构也有棵二叉树-代码详解-Toy模板网

这篇具有很好参考价值的文章主要介绍了【二叉树】大学有棵树叫高数,数据结构也有棵二叉树-代码详解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

二叉树

普通二叉树增删查改没有什么价值，因为用来存数据，太复杂了

价值体现

1.搜索二叉树(最多查找高度次) ，平衡搜索二叉树，ALV树红黑树 B 树 ->最坏情况O(N)

2.哈夫曼树

二叉树结构

以存放字符为例子

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* right;//指向左孩子
	struct BinaryTreeNode* left;//指向右孩子
	BTDataType data;//存放数据
}BTNode;

快速构建一颗二叉树

树的结构

【二叉树】大学有棵树叫高数,数据结构也有棵二叉树-代码详解

BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	else
	{
		newnode->data = x;
		newnode->left = NULL;
		newnode->right = NULL;
	}
	return newnode;
}


BTNode* BuyTree()
{
	//构建一颗二叉树
    //1.创建结点
	BTNode* nodeA = BuyNode('A');
	BTNode* nodeB = BuyNode('B');
	BTNode* nodeC = BuyNode('C');
	BTNode* nodeD = BuyNode('D');
	BTNode* nodeE = BuyNode('E');
	BTNode* nodeF = BuyNode('F');

	//2.链接
	nodeA->left = nodeB;
	nodeA->right = nodeC;

	nodeB->left = nodeD;

	nodeC->left = nodeE;
	nodeC->right = nodeF;

	return nodeA;
}
//        A
//	   B        C
//	D   NULL  E  F

前序遍历

前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。

前序遍历：根 - 左子树 - 右子树

//前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return ;
	}
	printf("%c ", root->data);//根
	PreOrder(root->left);//左子树
	PreOrder(root->right);//右子树
}

图解

【二叉树】大学有棵树叫高数,数据结构也有棵二叉树-代码详解

中序遍历

中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。

小技巧：把整棵二叉树投影到一条直线的顺序就是中序遍历的结果

中序遍历：左子树 - 根- 右子树

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);//左子树
	printf("%c ", root->data);//根
	InOrder(root->right);//右子树
}

后序遍历

后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后

后序遍历：左子树 - 右子树 -根

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);//遍历左子树
	PostOrder(root->right);//遍历右子树
	printf("%c ", root->data);//根
}

层序遍历

借助队列的特点：先进先出

核心思想：上一层带下一层

实现

1.根节点进队列

2.当前结点出来时，把它的左孩子和右孩子都带进去队列，这样上一层结点出的时候，带入下一层的结点

3.当队列为空，说明最后一层没有结点了，遍历结束

【二叉树】大学有棵树叫高数,数据结构也有棵二叉树-代码详解

//队列存放的是二叉树结点的地址
//层序遍历
void LevelOrder(BTNode* root)
{
	//空树就直接返回
	if (root == NULL)
	{
		return;
	}
	Queue q;
	QueueInit(&q);

	//根节点先入队列
	QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);//得到队头的节点

		QueuePop(&q);//出队头数据

		printf("%c ", front->data);

		//把左孩子和右孩子都带进队列
		//因为左孩子和右孩子不一定存在，所以要判断
		if (front->left)
		{
			QueuePush(&q, front->left);//入的是结点的地址
		}

		if (front->right)
		{
			QueuePush(&q, front->right);//入的是结点的地址
		}
	}
	printf("\n");
	//使用完队列之后要记得销毁
	QueueDestory(&q);
}

注意点

1.队列声明的问题

如果写成这样：err

【二叉树】大学有棵树叫高数,数据结构也有棵二叉树-代码详解

原因：**编译器不认识BTNode **

解决方法：在前面先声明。编译器的查找语法是往上找

解决：加一个前置声明

【二叉树】大学有棵树叫高数,数据结构也有棵二叉树-代码详解

声明只是告诉告诉编译器这个是结构体

队列中存放的是二叉树结点指针

2.Pop只是把指向结点的指针出队，二叉树结点并没有被删除

计算二叉树结点个数

二叉树可以为空树所以不用断言

空树结点个数：0

方法1：遍历计数思想

使用局部变量 —不可行

int  BinaryTreeSize(BTNode* root)
{
    //如果是空树返回0
    if(root == NULL)
    {
        return 0;
    }
    int count = 0;
    count++;
    BinaryTreeSize(root->left);//递归左子树计数
    BinaryTreeSize(root->right);//递归右子树计数
    return count;
}

每次递归开辟新的栈帧，所以count变量不是同一个,并不是对同一个count进行++

方法2：使用static 或者全局变量 —可行

//方式2：全局变量
int count = 0;
int  BinaryTreeSize(BTNode* root)
{
    //如果是空树返回0
    if(root == NULL)
    {
        return 0;
    }
    //方式1：使用static修饰  静态变量
    //static int count = 0;
       
    //本质是前序遍历
    count++;
    BinaryTreeSize(root->left);//递归左子树计数
    BinaryTreeSize(root->right);//递归右子树计数
    return count;
}

这种方式可行，但是如果再次调用此函数就会发生错误。因为count的值会叠加

方法3：在外部传址，然后遍历

int  BinaryTreeSize(BTNode* root,int* pn)
{
    if(root == NULL)
    {
        return 0;
    }
    (*pn)++;
        BinaryTreeSize(root->left,pn);//递归左子树计数
    BinaryTreeSize(root->right,pn);//递归右子树计数
}

方法4：通过返回值带回

二叉树结点个数 = 左子树结点个数 + 右子树的结点个数 + 根本身(1)

//二叉树结点个数
int  BinaryTreeSize(BTNode* root)
{
	//结点个数 = 根 + 左子树结点个数 + 右子树结点个数
    //如果根为空(空树)->返回0
	return root == NULL ? 0 : BinaryTreeSize(root->left)
		+ BinaryTreeSize(root->right) + 1;
}

求叶子结点个数

叶子结点的特点：左子树和右子树都为空

如何求叶子结点个数

思路：二叉树的叶子结点个数 = 左子树的叶子结点个数 + 右子树的叶子结点个数

//二叉树叶子结点个数
int  BinaryTreeLeafSize(BTNode* root)
{
	//如果空树->没有叶子结点，返回0
	if (root == NULL)
	{
		return 0;
	}
	//如果左子树和右子树都为空->就是叶子
	if ((root->left == NULL) && (root->right == NULL))
	{
		return 1;
	}
    //遍历左子树和右子树求叶子结点
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

求第K层结点个数

核心思路：

求第k层结点 ->转化求左子树的第K-1层结点个数 + 右子树的第K-1层结点个数

【二叉树】大学有棵树叫高数,数据结构也有棵二叉树-代码详解

//求第K层结点个数
int BinaryTreeLevelSize(BTNode* root,int k)
{
	//求第K层结点个数 == >转化为求第K-1层的左子树和右子树的结点个数
	if (root == NULL)
	{
		return 0;
	}
    //当递归到k = 1层时，就是要求的那一层的结点个数,如果是结点就会返回1，否则就是NULL，在上面返回0
	if (1 == k)  //防止写成k = 1
	{
		return 1;
	}
    //递归左子树和右子树的k-1层
	return BinaryTreeLevelSize(root->left, k - 1)
		+ BinaryTreeLevelSize(root->right, k - 1);
	
}

求二叉树的深度

思路：当前数的高度/深度 = 左子树的深度和右子树的深度的较大者 + 1

【二叉树】大学有棵树叫高数,数据结构也有棵二叉树-代码详解

不断递归下去，然后把左子树和右子树的高度较大者返回给上一层，就是左子树/右子树的高度

然后根结点再+1就是树的高度

效率低的写法：

//二叉树的高度/深度
int BinaryTreeDepth(BTNode* root)
{ 
	//二叉树的深度 = 左子树的深度和右子树的深度的较大者 +1(根节点)

    //空树返回0
	if (root == NULL)
	{
		return 0;
	}

	return BinaryTreeDepth(root->left) > BinaryTreeDepth(root->right)? BinaryTreeDepth(root->left)  + 1 : BinaryTreeDepth(root->right) + 1;//返回左子树和右子树的较大者+1
}

由于递归算出左树和右树的深度没有保存结果，还得再算一次,效率太低

效率高的写法

保存左树的高度和右树的高度

//二叉树的高度/深度
int BinaryTreeDepth(BTNode* root)
{ 
	//二叉树的深度 = 左子树的深度和右子树的深度的较大者 +1(根节点)

    //空树返回0
	if (root == NULL)
	{
		return 0;
	}
	int LeftDepth = BinaryTreeDepth(root->left);//计算左子树的高度
	int RightDepth = BinaryTreeDepth(root->right) ;//计算右子树的高度

	return LeftDepth > RightDepth ? LeftDepth + 1 : RightDepth + 1;//返回左子树和右子树的较大者+1
    
    //或者写成：
    //return fmax(BinaryTreeDepth(root->left),BinaryTreeDepth(root->right));
}

fmax和fmin

作用：返回两个浮点参数种较大/较小的一个要引用#include<math.h>头文件

查找值为x的结点

思路

1.如果是空树(根为空) 返回NULL

2.如果root结点不是我们要找的，先到左树去找，左树找不到，再去右树找

3.如果左树和右树都找不到，说明树中没有值为x的结点 ->返回NULL

错误想法

BTNode* BinaryTreeFind(BTNode* root,BTDataType x)
{
    //空树返回NULL
    if(root == NULL)
    {
        return NULL;
    }
    if(root ->data == x)
    {
        return root;
    }
    BinaryTreeFind(root->left,x);
    BinaryTreeFind(root->right,x);
}

报错

不是所有路径都有返回值

递归图解

【二叉树】大学有棵树叫高数,数据结构也有棵二叉树-代码详解

原因：递归返回的是上一层调用的地方，这样不一定能返回到最外层

递归带返回值的不可以写成这样，带返回值的递归：后面都要有返回值

注意：如果在左子树或者右子树找到了就会返回地址，找不到就返回NULL

所以如果左子树不为空，或者右子树不为空，说明找到了

效率低的写法

if(BinaryTreeFind(root->left,x))
{
    return BinaryTreeFind(root->left,x);
}
if(BinaryTreeFind(root->right,x))
{
    return BinaryTreeFind(root->right,x);
}

写成这样效率太低没保存结果导致要多算一遍

保存左树和右树的返回值

按照前序遍历的顺序查找

下一层递归的结果返给上一层，然后上一层依据这个结果判断要不要去右子树找…不断迭代，直到把整棵树都找完/在左树/右树/根找到了

递归图解

【二叉树】大学有棵树叫高数,数据结构也有棵二叉树-代码详解

在左子树找不到->去右子树找

整颗树都找不到->返回NULL

//查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root,BTDataType x)
{
	//空树返回NULL
	if (root == NULL)
	{
		return NULL;
	}
	//思路： 先判断根的值是不是x 不是的话 去左子树找  左子树找不到再去右子树找 (类似前序遍历)
	if (root->data == x)
	{
		return root;
	}
	//去左子树寻找
	BTNode* left = BinaryTreeFind(root->left,x);
	//如果左子树不为空 说明找到了
	if (left)
	{
		return left;
	}
	
	//左子树找不到就去右子树寻找
	BTNode* right = BinaryTreeFind(root->right, x);
	//如果右子树不为空 说明找到了
	if (right)
	{
		return right;
	}


	//注意！！！如果在整棵树都找不到 ->返回NULL
	return NULL;
}

效率低的写法

	//去左子树寻找
	BTNode* left = BinaryTreeFind(root->left,x);
	//左子树找不到就去右子树寻找
	BTNode* right = BinaryTreeFind(root->right, x);

	//如果左子树不为空 说明找到了
	if (left)
	{
		return left;
	}
	
	//如果右子树不为空 说明找到了
	if (right)
	{
		return right;
	}

这样写效率也低。因为如果在左子树找到了，就不用在右子树找了。

关于二叉树递归应该注意的问题：

1.带返回值的递归结果不能舍弃：

如查找值x的结点时的递归

2.防止重复递归

如：计算叶子结点个数

解决方法:把值保存起来

3.防止多查找

如：查找值x的结点时的递归，左子树找到了，就不需要在右子树查找

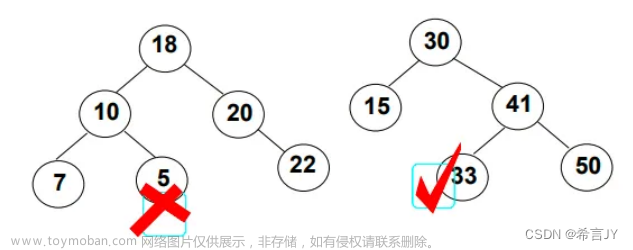
判断二叉树是否是完全二叉树

完全二叉树和非完全二叉树的区别：

层序遍历时：

完全二叉树的非空结点是连续的

非完全二叉树的非空结点是不连续的

思路

【二叉树】大学有棵树叫高数,数据结构也有棵二叉树-代码详解

层序遍历：
- 当遇到空指针跳出循环，检查后面的元素,如果后面有一个结点不是空，说明不是完全二叉树
- 如果后面的元素全部都是空指针->就是完全二叉树
后面的数据全部为空才是完全二叉树，后面空结点连续不一定是完全二叉树

注意：

完全二叉树也可以是空的(没有结点) 二叉排序树自然也可以是空的满二叉树同样可以是空的

//判断是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	//空树是完全二叉树
	if (root == NULL)
	{
		return true;
	}

	//层序遍历 遇到空结点则跳出

	Queue q;//创建队列，队列存放的是二叉树结点的指针 
	QueueInit(&q);//队列初始化
	QueuePush(&q, root);//先入根节点
	
	while (!QueueEmpty(&q))
	{
		BTNode* front =QueueFront(&q);
		QueuePop(&q);
		//如果遇到空了，就可以跳出，比较后面的结点
		if (front == NULL)
		{
			break;
		}
		//否则把左孩子和右孩子带进来,空结点也要带进队列
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}

	//遇到空指针了，break/队列为空跳出，判断后面的元素
	//1.剩下的全是空，则是完全二叉树
	//2.剩下的存在非空，说明不是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//如果有一个不为空->不是完全二叉树，返回false
		if (front !=NULL )
		{
			//返回都要先销毁：
			QueueDestory(&q);
			return false;
		}
	}

	//注意：最后要销毁队列
	QueueDestory(&q);

	//如果全部都为空，while跳出循环
	return true;
}

二叉树销毁

如果传一级指针，root结点置空了也没有用，要在外部再置空

free(root)有用，释放的是root指向的空间的内容

但是 root = NULL 没用，因为传的是一级指针，相当于传值，并不会真实改变root的指向

前序：如果先释放根就找不到左右了要先保存左右

中序：释放左之后释放根，就找不到右了

所以使用后序的方式释放更好，先释放左再释放右，最后释放根

//二叉树的销毁
void BinaryTreeDestory(BTNode* root)
{
	//可以为空树，所以不用断言空树直接返回
    if(root == NULL)
    {
        return;
    }
    
	//使用后序销毁,防止找不到根
	free(root->left);
	free(root->right);
	free(root);
    root = NULL;//没作用，在外部再置空
}

//外部
BTNode* root = BuyTree();
BinaryTreeDestory(root);
root = NULL;

方式2：传二级指针

void BinaryTreeDestory(BTNode** root)
    
    
//外部
  BTNode* root = BuyTree();
  BinaryTreeDestory(&root);

BinaryTree.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* right;//指向左孩子
	struct BinaryTreeNode* left;//指向右孩子
	BTDataType data;//存放数据
}BTNode;

//前序遍历
void PreOrder(BTNode* root);

//中序遍历
void InOrder(BTNode* root);

//后序遍历
void PostOrder(BTNode* root);

//二叉树的销毁
void BinaryTreeDestory(BTNode* root);

//二叉树叶子结点个数
int  BinaryTreeLeafSize(BTNode* root);

//二叉树结点个数
int  BinaryTreeSize(BTNode* root);


//求第K层结点个数
int BinaryTreeLevelSize(BTNode* root, int k);

//二叉树的高度/深度
int BinaryTreeDepth(BTNode* root);

//查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);

BinaryTree.c

#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include"BTree.h"

//前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return ;
	}
	printf("%c ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}

//二叉树的销毁
void BinaryTreeDestory(BTNode* root)
{
	assert(root);
	//保存根
	BTNode* cur = root;
	//使用后序销毁
	free(root->left);
	free(root->right);
	free(root);
}

//二叉树结点个数
int  BinaryTreeSize(BTNode* root)
{
	//结点个数 = 根 + 左子树结点个数 + 右子树结点个数
	return root == NULL ? 0 : BinaryTreeSize(root->left)
		+ BinaryTreeSize(root->right) + 1;
}

//二叉树叶子结点个数
int  BinaryTreeLeafSize(BTNode* root)
{
	//叶子结点：做左子树和右子树都为空
	if (root == NULL)
	{
		return 0;
	}
	//如果左子树和右子树都为空->就是叶子
	if ((root->left == NULL) && (root->right == NULL))
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}


//求第K层结点个数
int BinaryTreeLevelSize(BTNode* root,int k)
{
	//求第K层结点个数 == >转化为求第K-1层的左子树和右子树的结点个数
	if (root == NULL)
	{
		return 0;
	}
	if (1 == k)  //防止写成k = 1
	{
		return 1;
	}
	return BinaryTreeLevelSize(root->left, k - 1)
		+ BinaryTreeLevelSize(root->right, k - 1);
	
}

//二叉树的高度/深度
int BinaryTreeDepth(BTNode* root)
{ 
	//二叉树的深度 = 左子树的深度和右子树的深度的较大者 +1(根节点)

	if (root == NULL)
	{
		return 0;
	}
	int LeftDepth = BinaryTreeDepth(root->left) ;
	int RightDepth = BinaryTreeDepth(root->right) ;

	return LeftDepth > RightDepth ? LeftDepth + 1 : RightDepth + 1;
}

//查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root,BTDataType x)
{
	//空树返回NULL
	if (root == NULL)
	{
		return NULL;
	}
	//思路： 先判断根的值是不是x 不是的话 去左子树找  左子树找不到再去右子树找 (类似前序遍历)
	if (root->data == x)
	{
		return root;
	}
	//去左子树寻找
	BTNode* left = BinaryTreeFind(root->left,x);
	//如果左子树不为空 说明找到了
	if (left)
	{
		return left;
	}
	
	//左子树找不到就去右子树寻找
	BTNode* right = BinaryTreeFind(root->right, x);
	//如果右子树不为空 说明找到了
	if (right)
	{
		return right;
	}


	//注意！！！如果在整棵树都找不到 ->返回NULL
	return NULL;
}

test.c

#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include"BTree.h"


BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	else
	{
		newnode->data = x;
		newnode->left = NULL;
		newnode->right = NULL;
	}
	return newnode;
}

BTNode* BuyTree()
{
	//构建一颗二叉树
    //1.创建结点
	BTNode* nodeA = BuyNode('A');
	BTNode* nodeB = BuyNode('B');
	BTNode* nodeC = BuyNode('C');
	BTNode* nodeD = BuyNode('D');
	BTNode* nodeE = BuyNode('E');
	BTNode* nodeF = BuyNode('F');

	//2.链接
	nodeA->left = nodeB;
	nodeA->right = nodeC;

	nodeB->left = nodeD;

	nodeC->left = nodeE;
	nodeC->right = nodeF;

	return nodeA;

//        A
//	   B        C
//	D   NULL  E  F
}
int main()
{
	BTNode* root = BuyTree();
	PreOrder(root); //测试前序
	printf("\n");
	InOrder(root);//测试中序
	printf("\n");

	PostOrder(root);//测试后序
	printf("\n");
	printf("TreeSize = %d\n", BinaryTreeSize(root));
	printf("TreeLeafSize = %d\n", BinaryTreeLeafSize(root));

	printf("以A为根结点，第%d层结点个数为:%d\n", 2, BinaryTreeLevelSize(root, 2));
	printf("以A为根结点，第%d层结点个数为:%d\n", 3, BinaryTreeLevelSize(root, 3));
	printf("二叉树的高度为：%d\n",BinaryTreeDepth(root));

	
	BinaryTreeDestory(root);
	return 0;
}

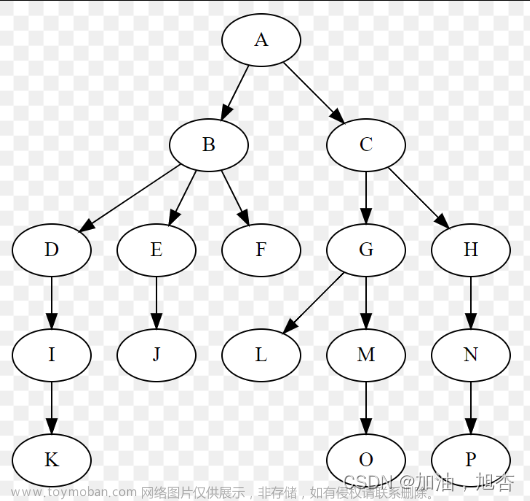
层序遍历+判断完全二叉树(test2.C)

构建出的树的结构

【二叉树】大学有棵树叫高数,数据结构也有棵二叉树-代码详解文章来源地址https://www.toymoban.com/news/detail-400445.html

#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include<stdio.h>
#include"Queue.h"


BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	else
	{
		newnode->data = x;
		newnode->left = NULL;
		newnode->right = NULL;
	}
	return newnode;
}

BTNode* BuyTree()
{
	//构建一颗二叉树
	//1.创建结点
	BTNode* nodeA = BuyNode('A');
	BTNode* nodeB = BuyNode('B');
	BTNode* nodeC = BuyNode('C');
	BTNode* nodeD = BuyNode('D');
	BTNode* nodeE = BuyNode('E');
	BTNode* nodeF = BuyNode('F');

	//2.链接
	nodeA->left = nodeB;
	nodeA->right = nodeC;

	nodeB->left = nodeD;

	nodeC->left = nodeE;
	nodeC->right = nodeF;

	return nodeA;
}
//        A
//	   B        C
//	D   NULL  E  F

//队列存放的是二叉树结点的地址
//层序遍历
void LevelOrder(BTNode* root)
{
	//空树就直接返回
	if (root == NULL)
	{
		return;
	}
	Queue q;
	QueueInit(&q);

	//根节点先入队列
	QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);//得到队头的节点

		QueuePop(&q);//出队头数据

		printf("%c ", front->data);

		//把左孩子和右孩子都带进队列
		//因为左孩子和右孩子不一定存在，所以要判断
		if (front->left)
		{
			QueuePush(&q, front->left);//入的是结点的地址
		}

		if (front->right)
		{
			QueuePush(&q, front->right);//入的是结点的地址
		}
	}
	printf("\n");
	//使用完队列之后要记得销毁
	QueueDestory(&q);
}

//判断是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	//空树是完全二叉树
	if (root == NULL)
	{
		return true;
	}

	//层序遍历 遇到空结点则跳出

	Queue q;//创建队列，队列存放的是二叉树结点的指针 
	QueueInit(&q);//队列初始化
	QueuePush(&q, root);//先入根节点
	
	while (!QueueEmpty(&q))
	{
		BTNode* front =QueueFront(&q);
		QueuePop(&q);
		//如果遇到空了，就可以跳出，比较后面的结点
		if (front == NULL)
		{
			break;
		}
		//否则把左孩子和右孩子带进来,空结点也要带进队列
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
	}

	//遇到空指针了，break/队列为空跳出，判断后面的元素
	//1.剩下的全是空，则是完全二叉树
	//2.剩下的存在非空，说明不是完全二叉树
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//如果有一个不为空->不是完全二叉树，返回false
		if (front !=NULL )
		{
			//返回都要先销毁：
			QueueDestory(&q);
			return false;
		}
	}

	//注意：最后要销毁队列
	QueueDestory(&q);

	//如果全部都为空，while跳出循环
	return true;
}
int main()
{
	BTNode* root = BuyTree();
	LevelOrder(root);
	bool tmp = BinaryTreeComplete(root);
	if (tmp)
	{
		printf("yes\n");
	}
	else
	{
		printf("No\n");
	}
	return 0;
}

Queue.c

#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include"Queue.h"

//初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = NULL;
	pq->tail = NULL;

}

//销毁
void QueueDestory(Queue* pq)
{
	assert(pq);
	//链表要遍历销毁结点，不能直接销毁
	QueueNode* cur = pq->head;
	while (cur)
	{
		//保存下一个结点
		QueueNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = NULL;
	pq->tail = NULL;
}

//队尾入数据
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	//相当于尾插

	//构建新结点
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	newnode->next = NULL;
	newnode->data = x;
	//情况1：链表为空
	if (pq->tail == NULL)
	{
		pq->head = pq->tail = newnode;
	}

	//情况2：
	//tail newnode 
	else
	{
		pq->tail->next = newnode; //尾插
	//注意如果一开始没有数据，pq->tail = NULL，此时会出错，相当于对空指针解引用
	//所以没有数据时需要单独判断
		pq->tail = newnode;//指向新的尾
	}

}

//队头出数据
void QueuePop(Queue* pq)
{
	assert(pq);
	//情况1：链表为空
	/*if (pq->head == NULL)
	{
		return -1;
	}*/
	assert(!QueueEmpty(pq));

	//情况2
	QueueNode* next = pq->head->next;//保存下一个结点
	free(pq->head);//释放队头
	pq->head = next;//next成为新的队头

	//注意！！！！如果一直删，删最后一个时候 此时next为NULL的,如果不把tail也置空，就会造成野指针
	if (pq->head == NULL)
	{
		pq->tail = NULL;
	}
}

//取队头数据
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	//链表为空
	/*if (pq->head == NULL)
	{
		return -1;
	}*/
	assert(!QueueEmpty(pq));
	return pq->head->data;
}

//取队尾数据
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->tail->data;
}

//队列的长度
int QueueSize(Queue* pq)
{
	assert(pq);
	//方法1：遍历统计
	//方法2：定义结构体时添加一个size变量，入数据：size++ 出数据size -- 用size标志队列长度

	//遍历统计
	QueueNode* cur = pq->head;
	int count = 0;
	while (cur)
	{
		count++;
		cur = cur->next;
	}
	return count;
}

//判断队列是否为空
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	/*if (pq -> head == NULL)
	{
		return true;
	}
	else
	{
		return false;
	}*/
	return pq->head == NULL;
}

Queue.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

//队列 - 先进先出 

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* right;//指向左孩子
	struct BinaryTreeNode* left;//指向右孩子
	BTDataType data;//存放数据
}BTNode;


typedef BTNode* QDataType;  //队列存放的是二叉树结点的地址

//队列中的结构体
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QueueNode;

//存放指向结构体的两个指针
typedef struct Queue
{
	QueueNode* head;//指向的头
	QueueNode* tail;//指向的尾
}Queue;

//初始化
void QueueInit(Queue* pq);

//销毁
void QueueDestory(Queue* pq);

//队尾入数据
void QueuePush(Queue* pq, QDataType x);

//队头出数据
void QueuePop(Queue* pq);

//取队头数据
QDataType QueueFront(Queue* pq);

//取队尾数据
QDataType QueueBack(Queue* pq);

//队列的长度
int QueueSize(Queue* pq);

//判断队列是否为空
bool QueueEmpty(Queue* pq);