典型相关分析（Canonical Correlation Analysis，CCA）原理及Python、MATLAB实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了典型相关分析（Canonical Correlation Analysis，CCA）原理及Python、MATLAB实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

随着对CCA的深入研究，是时候对CCA进行一下总结了。

~~本菜鸡~~主要研究方向为故障诊断，故会带着从应用角度进行理解。

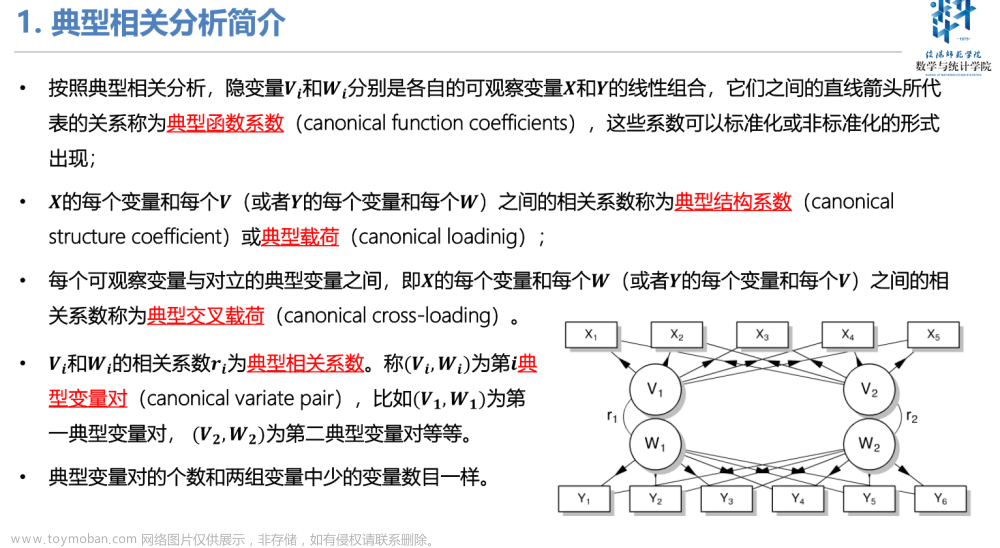
典型相关分析

基本原理

从字面意义上理解CCA，我们可以知道，简单说来就是对不同变量之间做相关分析。较为专业的说就是，一种度量两组变量之间相关程度的多元统计方法。

关于相似性度量距离问题，在这里有一篇Blog可以参考参考。

首先，从基本的入手。

当我们需要对两个变量 $X ， Y$ 进行相关关系分析时，则常常会用到相关系数来反映。学过概率统计的小伙伴应该都知道的吧。还是解释一下。

相关系数：是一种用以反映变量之间相关关系密切程度的统计指标。相关系数是按积差方法计算，同样以两变量与各自平均值的离差为基础，通过两个离差相乘来反映两变量之间相关程度；着重研究线性的单相关系数。
$Y)=\frac{\operatorname{Cov}(X, Y)}{\sqrt{\operatorname{Var}[X] \operatorname{Var}[Y]}}$
其中， $C o v (X, Y)$ 表示 $X, Y$ 的协方差矩阵， $V a r [X]$ 为 $X$ 的方差， $V a r [Y]$ 为 $Y$ 的方差.

复习了一下大学本科概率统计知识，那么，如果我们需要分析的对象是两组或者多组向量，又该怎么做呢？

CCA的数学表达

这里举例两组变量 $A(a_1,a_2,...,a_n),B(b_1,b_2,...,b_m)$ ，那么我们的公式会是这样：
$R(X_i,Y_j)=\sum_{i=1,j=1}^{n,m} \frac{Cov(X_i,Y_j)}{\sqrt{Var[X_i]Var[Y_j]}}$
我们会得到一个这样的矩阵：
$\begin{bmatrix} R(X_1,Y_1) &... & R(X_1,Y_{m-1}) & R(X_1,Y_m)\\R(X_2,Y_1) & ...& R(X_2,Y_{m-1})& R(X_2,Y_m)\\ ...& ...& ...&... \\ R(X_n,Y_1) & ...& ...&R(X_n,Y_m) \end{bmatrix}$

这样的话，我们把每个变量的相关系数都求了出来，不知道会不会和我一样觉得这样很繁琐呢。如果我们能找到两组变量之间的各自的线性组合，那么我们就只分析讨论线性组合之间的相关分析。

典型相关系数：是先对原来各组变量进行主成分分析，得到新的线性关系的综合指标，再通过综合指标之间的线性相关系数来研究原各组变量间相关关系。

现在我们利用主成分分析（PCA）的思想，可以把多个变量与多个变量之间的相关转化成两个变量之间的相关。

先得到两组变量 $A^T,B^T)$ 的协方差矩阵
$\Sigma=\left[\begin{array}{l} \Sigma_{11} \ \Sigma_{12} \\ \Sigma_{21} \ \Sigma_{22} \end{array}\right]$
其中， $\Sigma_{11} = Cov(A),\Sigma_{22} = Cov(B),\Sigma_{12}=\Sigma_{12}^T = Cov(A,B)$ .

把上面两组变量 $A(a_1,a_2,...,a_n),B(b_1,b_2,...,b_m)$ 分别组合成两个变量U、V，则用线性表示
$\begin{matrix} U=t_1a_1+t_2a_2+...+t_na_n,\\ \\V=h_1b_1+h_2b_2+...+h_mb_m \end{matrix}$

然后，找出最大可能的相关系数 ${t_k}=(t_1,t_2,...,t_n)^T,{h_k}=(h_1,h_2,...,h_m)^T$ ,

使得， $R(U,V)\longrightarrow Max$ ，这样，就得到了典型相关系数；而其中的 $U, V$ 为典型相关变量。

典型相关分析最朴素的思想：首先分别在每组变量中找出第一对典型变量，使其具有最大相关性，然后在每组变量中找出第二对典型变量，使其分别与本组内的第一对典型变量不相关，第二对本身具有次大的相关性。如此下去，直到进行到K步，两组变量的相关系被提取完为止，可以得到K组变量。

So，

注意：此时的 $(U, V)$ 若不能反映两组变量之间的相关关系，我们需要继续构造下一组关系变量来表示，具体可构造 $K$ 对这样的关系

直到 $R(U,V)\longrightarrow Max$ 为止
$\begin{matrix} U_k={t_k^T}{A}=t_{1k}a_1+t_{2k}a_2+...+t_{nk}a_n\\ \\ V_k={h_k^T}{B}=h_{1k}b_1+h_{2k}b_2+...+h_{mk}b_m \end{matrix}$

其中，我们需要一个约束条件满足，使得 $R(U,V)\longrightarrow Max$

$\begin{matrix} Var(U_k)=Var({t_k^T}{A})={t_k^T}\Sigma_{11}t_k=1\\ \\ Var(V_k)=Var({h_k^T}{A})={h_k^T}\Sigma_{22}h_k=1\\ \\ Cov（U_k,U_i）=Cov(U_k,V_i)=Cov(V_i,U_k)=Cov(V_k,V_i)=0(1<=i<k) \end{matrix}$
典型相关系数公式 $R_{(U,V)}$
$R_{(U,V)}=\frac{\operatorname{Cov}(U, V)}{\sqrt{\operatorname{Var}[U] \operatorname{Var}[V]}}=Cov(U,V)={t_k}^TCov(A,B)h_k={t_k}^T\Sigma_{12} h_k$

在此约束条件下， $t_k,h_k$ 系数得到最大，则使得 $R_{(U,V)}$ 最大。

典型相关系数及变量的求法

下面一起来求 $t_1,h_1$ （这里只例举第一典型相关系数）

（一起来复习高数–拉格朗日乘数法）

前提条件，我们有个计算公式，约束条件也有了，故这是一个求解条件极值题呀！！！

列出我们的拉格朗日函数：
$\phi\left(t_{1}, h_{1}\right)=t_{1}^T \Sigma_{12} h_{1}-\frac{\lambda}{2}\left(t_{1}^T \Sigma_{11} t_{1}-1\right)-\frac{v}{2}\left(h_{1}^T \Sigma_{22} h_{1}-1\right)$
其中， $\lambda,v$ 表示拉格朗日乘子参数。

由上述典型相关系数公式 $R_{(U,V)}$ 可知，我们只需求其系数 $t_1,h_1$ 的最大值，即可

对 $\phi(t_1,h_1)$ 做一阶偏导运算：
$\left\{\begin{array}{l} \frac{\partial \phi}{\partial t_{1}}=\sum_{12} h_{1}-\lambda \sum_{11} t_{1}=0 \\ \\ \frac{\partial \phi}{\partial h_{1}}=\sum_{21} t_{1}-v \sum_{22} h_{1}=0 \end{array}\right.$
也就是
$\left\{\begin{array}{l} \sum_{12} h_{1}-\lambda \sum_{11} t_{1}=0 \\ \\ \sum_{21} t_{1}-v \sum_{22} h_{1}=0 \end{array}\right.$
将上式分别左乘 $t_1,h_1$ 得，
$\left\{\begin{array}{l} \ t_{1}\Sigma_{12} h_{1}-\lambda t_{1}\Sigma_{11} t_{1}=0 \\ \\ \ h_{1}\Sigma_{21} t_{1}-v h_{1} \Sigma_{22} h_{1}=0 \end{array}\right.$
由于约束条件可知 $Var(U_1)=Var(V_1)=1$ ，解得，
$\left\{\begin{array}{l} \ t_{1}\Sigma_{12} h_{1}=\lambda \\ \\ \ h_{1}\Sigma_{21} t_{1} =v \end{array}\right.$
此时，我们来对比一下上面列出的求解 $R_{(U,V)}$ 公式，有没有，是不是，一模一样，我们的拉格朗日乘子 $\lambda,v=t_{1}\Sigma_{12} h_{1}=R_{(U,V)}$ ，也就是说， $\lambda,v$ 即为我们要求解的典型相关系数。

我们由式 $\left\{\begin{array}{l} \sum_{12} h_{1}-\lambda \sum_{11} t_{1}=0 \\ \\ \sum_{21} t_{1}-v \sum_{22} h_{1}=0 \end{array}\right.$ ,可得
$\lambda t_1 = \Sigma _{11}^{-1}\Sigma_{12} h_{1}$
由于 $\lambda=v$ ，再将此代入 $\sum_{21} t_{1}-v \sum_{22} h_{1}=0$ 中，可得
$\begin{array}{l} \Sigma_{12} \Sigma_{22}^{-1} \Sigma_{21} t_{1}-\lambda^{2} \Sigma_{11} t_{1}=0 \\ \\ \Sigma_{11}^{-1} \Sigma_{12} \Sigma_{22}^{-1} \Sigma_{21} t_{1}-\lambda^{2} t_{1}=0 \end{array}$
上面的式子是不是很熟悉 $AX=\lambda X$ ,

$\Sigma_{11}^{-1} \Sigma_{12} \Sigma_{22}^{-1} \Sigma_{21} = A \\ t_1=X \\ \lambda=\lambda^2$
故， $\Sigma_{11}^{-1} \Sigma_{12} \Sigma_{22}^{-1} \Sigma_{21}$ 的特征值为 $\lambda^2$ ，特征向量为 $t_1$ 。

到此，我们可求得相应的 $t_1,h_1$ 及 $R_{(U,V)}$ 。

典型相关分析应用

基于 CCA 的故障检测方法

对于CCA应用在故障检测中，基于 CCA 的故障检测方法可以视为基于 PCA 和基于 PLS 故障检测方法的一种扩展。

基本思想：是利用典型相关关系构建一个残差发生器，通过对残差信号的评价做出故障检测的相应决策。该方法中提出了 4 个统计量，将输入空间分为两个部分，即与输出空间相关的子空间和与输出空间不相关的子空间；同理，将输出空间分为两个部分，即与输入空间相关的子空间和与输入空间不相关的子空间。

设 $u_{obs}∈Ｒ^l$ 和 $y_{obs}∈Ｒ^m$ 表示测量的过程输入和输出向量， $l$ 和 $m$ 分别表示相应的数据维数。对两个向量进行去均值，可得

$\boldsymbol{u} = \boldsymbol{u}_{\mathrm{obs}}-\boldsymbol{\mu}_{u} \tag{1}$
$\boldsymbol{y} = \boldsymbol{y}_{\mathrm{obs}}-\boldsymbol{\mu}_{y} \tag{2}$
式中: $μ_u$ 和 $μ_y$ 分别表示输入变量均值和输出变量均值。假设采样得到 N 个过程数据，并组成如下输入输出数据集

$\boldsymbol{U}=[\boldsymbol{u}(1), \boldsymbol{u}(2), \cdots, \boldsymbol{u}(N)] \in \mathbf{R}^{l \times N}, \boldsymbol{Y}=[\boldsymbol{y}(1), \boldsymbol{y}(2), \cdots, \boldsymbol{y}(N)] \in \mathbf{R}^{m \times N}$
式中： $u (i) ， y (i) ， (i = 1 ， \dots ， N)$ 是按式(1)(2)中心化后的输入输出向量，相应的平均值
$\boldsymbol{\mu}_{u} \approx \frac{1}{N} \sum_{i=1}^{N} \boldsymbol{u}_{\mathrm{obs}}(i), \boldsymbol{\mu}_{y} \approx \frac{1}{N} \sum_{i=1}^{N} \boldsymbol{y}_{\mathrm{obs}}(i),$

并且，协方差矩阵 $Σ_u、 Σ_y$ 和输入输出的互协方差矩阵 $Σ_{uy}$ 分别为:
$\boldsymbol{\Sigma}_{u} \approx \frac{1}{N-1} \sum_{i=1}^{N}\left(\boldsymbol{u}_{\mathrm{obs}}(i)-\boldsymbol{\mu}_{u}\right)\left(\boldsymbol{u}_{\mathrm{obs}}(i)-\boldsymbol{\mu}_{u}\right)^{\mathrm{T}}=\frac{\boldsymbol{U} \boldsymbol{U}^{\mathrm{T}}}{N-1}\tag{3}$
$\boldsymbol{\Sigma}_{y} \approx \frac{1}{N-1} \sum_{i=1}^{N}\left(\boldsymbol{y}_{\mathrm{obs}}(i)-\boldsymbol{\mu}_{y}\right)\left(\boldsymbol{y}_{\mathrm{obs}}(i)-\boldsymbol{\mu}_{y}\right)^{\mathrm{T}}=\frac{\boldsymbol{Y} \boldsymbol{Y}^{\mathrm{T}}}{N-1}\tag{4}$
$\boldsymbol{\Sigma}_{u y} \approx \frac{1}{N-1} \sum_{i=1}^{N}\left(\boldsymbol{u}_{\mathrm{obs}}(i)-\boldsymbol{\mu}_{u}\right)\left(\boldsymbol{y}_{\mathrm{obs}}(i)-\boldsymbol{\mu}_{y}\right)^{\mathrm{T}}=\frac{\boldsymbol{U} \boldsymbol{Y}^{\mathrm{T}}}{N-1}\tag{5}$
结合 CCA 方法，可得:
$\left(\frac{\boldsymbol{U} \boldsymbol{U}^{\mathrm{T}}}{N-1}\right)^{-1 / 2}\left(\frac{\boldsymbol{U} \boldsymbol{Y}^{\mathrm{T}}}{N-1}\right)\left(\frac{\boldsymbol{Y} \boldsymbol{Y}^{\mathrm{T}}}{N-1}\right)^{-1 / 2}=\boldsymbol{\Sigma}_{u}^{-1 / 2} \boldsymbol{\Sigma}_{u y} \boldsymbol{\Sigma}_{y}^{-1 / 2}=\boldsymbol{\Gamma}_{s} \boldsymbol{\Sigma} \boldsymbol{\Psi}_{s}^{\mathrm{T}}, \boldsymbol{\Sigma}=\left[\begin{array}{ll} \boldsymbol{\Lambda}_{\kappa} & 0 \\ 0 & 0 \end{array}\right]\tag{6}$
式中: κ 为主元个数， $κ ≤ min(l，m); Σ_κ= diag(ρ1， …， ρκ)$ 为典型相关系数值。
令 $\boldsymbol{J}_{s}=\boldsymbol{\Sigma}_{u}^{-1 / 2} \boldsymbol{\Gamma}(:, 1: \kappa), \boldsymbol{L}_{s}=\boldsymbol{\Sigma}_{y}^{-1 / 2} \boldsymbol{\Psi}(:, 1: \kappa), \boldsymbol{J}_{\mathrm{res}}=\boldsymbol{\Sigma}_{u}^{-1 / 2} \boldsymbol{\Gamma}(:, \kappa+1: l), \boldsymbol{L}_{\mathrm{res}}=\boldsymbol{\Sigma}_{y}^{-1 / 2} \boldsymbol{\Psi}(:, \kappa+1: m)$ ,

由 CCA 方法可知， $J^T_su$ 和 $L^T_sy$ 具有密切的相关性。

但是在实际系统中，测量变量难免受到噪声影响，两者之间的相关性可表示为:
$\boldsymbol{L}_{s}^{\mathrm{T}} \boldsymbol{y}(k)=\boldsymbol{\Lambda}_{\kappa}^{\mathrm{T}} \boldsymbol{J}_{s}^{\mathrm{T}} \boldsymbol{u}(k)+\boldsymbol{v}_{s}(k)\tag{7}$
式中: $v_s$ 为噪声项，并且与 $J^T_su$ 弱相关。基于此，残差向量
$\boldsymbol{r}_{1}(k)=\boldsymbol{L}_{s}^{\mathrm{T}} \boldsymbol{y}(k)-\boldsymbol{\Lambda}_{\kappa}^{\mathrm{T}} \boldsymbol{J}_{s}^{\mathrm{T}} \boldsymbol{u}(k)\tag{8}$

其中的 ${\Lambda}_{\kappa}^{\mathrm{T}}$ 为系数矩阵，上面介绍了CCA的数学运算，这里应该能理解，只不过多加了一个噪声向量。

假设输入输出数据服从高斯分布。已知线性变换不改变随机变量的分布，所以残差信号 $r_1$ 也服
从高斯分布，其协方差矩阵：
$\boldsymbol{\Sigma}_{r_1}=\frac{1}{N-1}\left(\boldsymbol{L}_{s}^{\mathrm{T}} \boldsymbol{Y}-\boldsymbol{\Lambda}_{\kappa}^{\mathrm{T}} \boldsymbol{J}_{s}^{\mathrm{T}} \boldsymbol{U}\right)\left(\boldsymbol{L}_{s}^{\mathrm{T}} \boldsymbol{Y}-\boldsymbol{\Lambda}_{\kappa}^{\mathrm{T}} \boldsymbol{J}_{s}^{\mathrm{T}} \boldsymbol{U}\right)^{\mathrm{T}}=\frac{\boldsymbol{I}_{\kappa}-\boldsymbol{\Lambda}_{\kappa}^{2}}{N-1}{ }^{}\tag{9}$
同理，还可以得到另一残差向量
$\boldsymbol{r}_{2}(k)=\boldsymbol{L}_{s}^{\mathrm{T}} \boldsymbol{y}(k)-\boldsymbol{\Lambda}_{\kappa}^{\mathrm{T}} \boldsymbol{J}_{s}^{\mathrm{T}} \boldsymbol{u}(k)\tag{10}$
其协方差矩阵
$\boldsymbol{\Sigma}_{r_2}=\frac{1}{N-1}\left(\boldsymbol{L}_{s}^{\mathrm{T}} \boldsymbol{Y}-\boldsymbol{\Lambda}_{\kappa}^{\mathrm{T}} \boldsymbol{J}_{s}^{\mathrm{T}} \boldsymbol{U}\right)\left(\boldsymbol{L}_{s}^{\mathrm{T}} \boldsymbol{Y}-\boldsymbol{\Lambda}_{\kappa}^{\mathrm{T}} \boldsymbol{J}_{s}^{\mathrm{T}} \boldsymbol{U}\right)^{\mathrm{T}}=\frac{\boldsymbol{I}_{\kappa}-\boldsymbol{\Lambda}_{\kappa}^{2}}{N-1}{ }^{}\tag{11}$
由式(9)(11) 可以看出，残差 r1和 r2的协方差相同。对于故障检测，可构造如下两个统计量:
$T_{1}^{2}(k)=(N-1) \boldsymbol{r}_{1}^{\mathrm{T}}(k)\left(\boldsymbol{I}_{\kappa}-\boldsymbol{\Lambda}_{\kappa}^{2}\right)^{-1} \boldsymbol{r}_{1}(k)\tag{12}$
$T_{2}^{2}(k)=(N-1) \boldsymbol{r}_{2}^{\mathrm{T}}(k)\left(\boldsymbol{I}_{\kappa}-\boldsymbol{\Lambda}_{\kappa}^{2}\right)^{-1} \boldsymbol{r}_{2}(k)\tag{13}$
注意到统计量 $T^2_1$ 用于检测发生在输出子空间且输入相关的那部分故障，为了检测与输入不相关的那部分故障，可构造一个统计量
$T_{3}^{2}=\boldsymbol{y}^{\mathrm{T}} \boldsymbol{L}_{\mathrm{res}} \boldsymbol{L}_{\mathrm{res}}^{\mathrm{T}} \boldsymbol{y}\tag{14}$
同理，为了检测发生在输入空间且与输出不相关的那部分故障，可构造另一统计量
$T_{4}^{2}=\boldsymbol{u}^{\mathrm{T}} \boldsymbol{L}_{\mathrm{res}} \boldsymbol{L}_{\mathrm{res}}^{\mathrm{T}} \boldsymbol{u}\tag{15}$
由以上分析可知，通过确定主元个数 κ，可以得到4 个统计量 $T^2_1$ 、 $T^2_2$ 、 $T^2_3$ 和 $T^2_4$ 进行故障检测。

关于过程故障监控的统计量 $T^2$ ，在深度学习、机器学习、故障诊断领域用的较多，这里可参考 $T^2$ 的相关内容。
应用部分参考自一篇Paper $\longrightarrow$ [1]. CHEN Zhiw en,DING S X,ZHANG Kai,et al.Canonical correlation analysis- based fault detection methods with application to alumina evaporation process[J].Control Engineering Practice,2016,46:51- 58．

Python代码：

## 通过sklearn工具包内置的CCA实现
import numpy as np
from sklearn.cross_decomposition import CCA
from icecream import ic   # ic用于显示，类似于print

A = [[3, 4, 5, 6, 7] for i in range(2000)] 
B = [[8, 9, 10, 11, 12] for i in range(2000)] 
# 注意在A、B中的数为输入变量及输出变量参数

# 建模
cca = CCA(n_components=1)  # 若想计算第二主成分对应的相关系数，则令cca = CCA(n_components=2)
# 训练数据
cca.fit(X, Y)
# 降维操作
X_train_r, Y_train_r = cca.transform(X, Y)
#输出相关系数
ic(np.corrcoef(X_train_r[:, 0], Y_train_r[:, 0])[0, 1])  #如果想计算第二主成分对应的相关系数 print(np.corrcoef(X_train_r[:, 1], Y_train_r[:, 1])[0, 1])

另有一个包含可视化CCA的Python代码在这里。

Matlab代码：

function[ccaEigvector1, ccaEigvector2] = CCA(data1, data2)


dataLen1 = size(data1, 2);

dataLen2 = size(data2, 2);

 

% Construct the scatter of each view and the scatter between them

data = [data1 data2];

covariance = cov(data);

% Sxx = covariance(1 : dataLen1, 1 : dataLen1) + eye(dataLen1) * 10^(-7);

Sxx = covariance(1 : dataLen1, 1 : dataLen1);

% Syy = covariance(dataLen1 + 1 : size(covariance, 2), dataLen1 + 1 : size(covariance, 2)) ...

% + eye(dataLen2) * 10^(-7);

Syy = covariance(dataLen1 + 1 : size(covariance, 2), dataLen1 + 1 : size(covariance, 2));

Sxy = covariance(1 : dataLen1, dataLen1 + 1 : size(covariance, 2));

% Syx = Sxy';

 
% using SVD to compute the projection

Hx = (Sxx)^(-1/2);

Hy = (Syy)^(-1/2);
 

H = Hx * Sxy * Hy;

[U, D, V] = svd(H, 'econ');

ccaEigvector1 = Hx * U;

ccaEigvector2 = Hy * V;

% make the canonical correlation variable has unit variance

ccaEigvector1 = ccaEigvector1 * diag(diag((eye(size(ccaEigvector1, 2)) ./ sqrt(ccaEigvector1' * Sxx * ccaEigvector1))));

ccaEigvector2 = ccaEigvector2 * diag(diag((eye(size(ccaEigvector2, 2)) ./ sqrt(ccaEigvector2' * Syy * ccaEigvector2))));

end