离散数学笔记整理（个人向）

1. 集合

1.1. 概念

• 等势：A、B两集合间存在一一对应的关系，则称A与B等势，记为 A ~ B。
• 可数集合：与自然数集合N等势的集合。集合基数为阿列夫零。包括：正奇数集合，质数集合，有理数集合Q。
• 不可数集合：与开区间(0, 1)等势的集合。集合基数为阿列夫。

集合A的基数记为card A

1.2. 特殊集合

自然数集N，有理数集Q，实数集R，空集∅，全集E，A的幂集P(A) = {x | x ⊆ A}

当A = ∅时，P(A) = {∅}

1.3. 集合运算

• 异或（对称差）：去掉两个集合交集的元素，再并起来

2. 命题逻辑

2.1. 联结词

1. 蕴涵联结词：P → Q

   • 如果P，则Q
   • 因为P，所以Q
   • 只要P，就Q
   • P仅当Q
   • 只有Q，才P
   • 除非Q，才P
   • 除非Q，否则¬P

2. 优先级：否定、合取∧、析取∨、蕴涵、等价

   ps. 当两个命题不同时成立时，异或可以用析取表示

2.2. 命题公式

分类：重言式（永真）、矛盾式（永假）、可满足式（有真）

2.3. 等价关系

• 等值式：若A ↔ B是重言式，则记为等值式A ⇔ B，也即A与B等价。
• 吸收律：G ∧ (G ∨ H) = G；G ∨ (G ∧ H) = G
• 蕴涵式：G → H = ¬G ∨ H
• 等价式：G ↔ H = (G → H) ∧ (H → G)

2.4. 范式

• 文字：命题变元或命题变元的否定
• 子句：文字析取构成
• 短语：文字合取构成
• 析取范式：由短语析取构成
• 合取范式：由子句合取构成
• 主析取范式：极小项，文字默认为真，真值表找1
• 主合取范式：极大项，文字默认为假，真值表找0

2.5. 推理

基本推理形式

• 推理有效：前提都为真，则结论为真。
• 判定定理：A₁，A₂，…，An → B为重言式，当且仅当A₁，A₂，…，An ⇒ B有效。
• 证明有效：
  1. 真值表法
  2. 等值演算法
  3. 主析取范式法（包含所有极小项则为重言式）

自然演绎法

• 概念：给若干前提，推出一个结论

• 推理定律：

  1. 附加律：A ⇒ A ∨ B或B ⇒ A ∨ B
  2. 简化律：A ∧ B ⇒ A或A ∧ B ⇒ B
  3. 假言推理：A → B，A ⇒ B
  4. 拒取式：A → B，¬B ⇒ ¬A
  5. 析取三段论：A ∨ B，¬B ⇒ A
  6. 假言三段论：A → B，B → C ⇒ A → C
  7. 构造性二难：A → B，C → D，A ∨ C ⇒ B ∨ D
  8. 破坏性二难：A → B，C → D，¬B ∨ ¬D ⇒ ¬A ∨ ¬C
  9. 合取引入：A，B ⇒ A ∧ B

• 推理规则（自然推理系统）：

  1. 规则P（前提引入规则）：推导过程中，可随时引入前提集合中任一个集合。
  2. 规则T（结论引入规则）：推导过程中，可随时引入由一个或多个前提推导出来的中间结果。
  3. 规则CP（置换规则）：如果能由前提集合Γ与公式P推出结论S，则能由Γ推出P → S。
  4. 上面八条推理定律形成的规则

• 证明推理：

  1. 直接证明法
  2. 附加前提证明法：用规则CP
  3. 归谬证明法（反证法）：将结论否定式作为前提，用直接证明法推出矛盾式。原理如下：
     ① 若证A₁，A₂，…，An ⇒ B
     ② 即证A₁，A₂，…，An → B为重言式
     ③ 又由蕴涵式：¬(A₁ ∧ A₂ ∧ … ∧ An) ∨ B为重言式
     ④ 由反证法：A₁ ∧ A₂ ∧ … ∧ An ∧ ¬B为矛盾式。

3. 谓词逻辑

3.1. 概念

• 个体、谓词、量词

• ∀x(P(x) → Q(x))：在个体域D中的任意x，如果其有性质P，则其就有性质Q。

  1. x是个体变元
  2. ∀x是全称量词（全称用→，存在用∧）
  3. P、Q是谓词，也被称为原子公式

  例：所有人都会说话。P：x是人。Q：x会说话。

• 公式：全称合式公式，原子公式是合式公式，¬P，P∨Q，P∧Q，P→Q，P↔Q都为合式公式，带量词的合式公式也是合式公式。

• 约束变元：个体变元x在使用变元x量词的辖域内，则称x为约束变元。

• 自由变元：不在辖域内则成为自由变元。

• 闭式：一个公式内无自由变元，则称该公式为闭式。

3.2. 谓词公式

分类：永真式（逻辑有效式）、矛盾式（永假式）、可满足式

3.3. 公式等价关系

• 等价：若公式P ↔ Q是永真式，则P ⇔ Q是等值式，也即公式P与公式Q等价。
• 共有：命题公式的等价关系在谓词公式中依然成立。
• 特有：P、Q含有变元x，S不含变元x
  1. 改名规则：∀xP(x) = ∀yP(y)；存在量词同理
  2. 量词转换律：¬∀xP(x) = ∃x¬P(x)；¬∃xP(x) = ∀x¬P(x)
  3. 量词辖域扩展/收缩律：
     • ∀x(P(x) ∧ S) = ∀xP(x) ∧ S；析取同理，存在量词同理。
     • ∀x(P(x) → S) = ∃xP(x) → S；存在量词同理。
     • ∀x(S → P(x)) = S → ∀xP(x)；存在量词同理。
  4. 量词分配律：
     • ∀x(P(x) ∧ Q(x)) = ∀xP(x) ∧ ∀xQ(x)
     • ∃x(P(x) ∨ Q(x)) = ∃xP(x) ∨ ∃xQ(x)
  5. 无法用量词分配的情况：
     • ∀xP(x) ∨ ∀xQ(x) = ∀x(∀y)(P(x) ∨ Q(y))
     • ∃xP(x) ∧ ∃xQ(x) = ∃x∃y(P(x) ∧ Q(y))

3.4. 范式

• 前束范式：将¬内移到原子公式前，量词在公式最前端。利用谓词公式等价关系将一个公式转化成前束范式。

  ps. 根据量词的辖域可以利用改名规则

3.5. 推理

推理形式

• 判定定理：类比于命题推理，A₁，A₂，…，An → B为永真式，当且仅当A₁，A₂，…，An ⇒ B有效。

推理定律

1. 命题的推理定律仍适用于谓词推理
2. 每个谓词逻辑的基本等值式，都可以推出两条推理定律，如由¬∀xP(x) = ∃x¬P(x)：
   ¬∀xP(x) ⇒ ¬P(x)；¬P(x) = ¬∀xP(x)
3. 两条特殊的定律：
   • ∀xP(x) ∨ ∀xQ(x) ⇒ ∀x(P(x) ∨ Q(x))
   • ∃x(P(x) ∧ Q(x)) ⇒ ∃xP(x) ∧ ∃xQ(x) 合取的存在推出存在的合取

推理规则（自然推理系统）

1. 命题中的所有推理规则
2. UI（全称消去规则，用于消去全称量词）：∀xP(x) ⇒ P©，c为任意个体常量；或∀xP(x) ⇒ P(y)，不产生歧义即可。
3. EI（存在消去规则）：
   • ∃xP(x) ⇒ P©，c为使P©为真的特定个体常量
   • ∃xP(x, y) ⇒ P(f(y), y)
4. UG（全称引入规则，用于引入全称量词）：P(y) ⇒ ∀xP(x)，不产生歧义即可
5. EG（存在引入规则）：P© ⇒ ∃xP(x)，c为特定个体常量；或P(x) ⇒ ∃yP(y)

• 推理过程：消去量词；命题推理；如果结论中有量词，则最后引入量词。
  如果消去量词同时用到了UI和EI，先用EI，再用UI（因为EI中的个体常量必须满足P© = 1，若先用UI，得到的个体常量不一定满足该条件）。
  若一个变量用EI规则消去量词，则其引入量词时只能用EG规则；而采用UI规则消去的，引入量词时UG和EG都可用。这是由规则的性质决定的。

4. 二元关系

4.1. 概念

• 有序对：<x, y>称为有序对，或序偶。

• 笛卡尔积：若有集合A，B，则集合A×B = {<x, y>|(x∈A)∧(y∈B)}是集合A与B的笛卡尔积。

  笛卡尔积不满足交换律与结合律，但对并交运算满足分配律。
  ∅与任意集合的笛卡尔积都是空集。

• 二元关系：要么是空集，要么是元素为有序对的集合，记为R。若<x, y>∈R，则记作xRy。A与B间关系的种类为$2^{|A|\cdot |B|}$，A上的关系的种类为$2^{|A|²}$。
  R的定义域domR，值域ranR，域fldR = domR ∪ ranR；A称为前域，B为后域。

• 几个重要关系：

  1. R = ∅，则R为空关系
  2. R = A×B，则R为A到B的全关系，记为$E_A$
  3. R = $I_A$ = {<x, x>|x∈A}，则R为A上的恒等关系

• 关系表示：枚举、图形、关系矩阵（是布尔矩阵）

4.2. 关系运算

• 布尔矩阵运算：交∧、并∨、积⊙（矩阵乘法）

• 关系运算：

  1. 并∪、交∩、差-、补。
  2. 复合R ◦ S：<x, y> ◦ <y, z> = <x, z>，是从A到C的关系；R和S关系矩阵作布尔积运算，得到结果即为R ◦ S的关系矩阵。
  3. 逆$R^{-1}$：<x, y>变为<y, x>；R的关系矩阵转置即为R的逆。
  4. 限制 R $\uparrow$ A = {<x, y> | x ∈ A ∧ xRy}
  5. 像 R[A] = ran(R | A)

• 运算性质：

  1. 复合运算结合律与同一律（$I_A$ ◦ R = R ◦ $I_A$ = R）
  2. 复合分配律：
     • R ◦ (S ∪ T) = R ◦ S ∪ R ◦ T，左复合同理
     • R ◦ (S ∩ T) ⊆ R ◦ S ∩ R ◦ T，左复合同理
  3. 逆运算：
     • $(R◦S{)}^{-1}$ = $S^{-1}$ ◦ $R^{-1}$
     • $(R\cup S{)}^{-1}$ = $R^{-1}$ ∪ $S^{-1}$，交和差同理
     • domR = $ran{R}^{-1}$，反之同理
  4. 幂运算：
     • R⁰ = $I_A$
     • $R^{m+n}$ = $R^m$ ◦ $R^n$
     • $(R^m{)}^n$ = $R^{mn}$
     • 收敛性
       

4.3. 关系性质

• 五个性质
  

  一个关系能同时具有多个性质，如$I_A$同时具有自反性，对称性，反对称性，传递性。

• 性质的保守性

  1. R，S自反，$R^{-1}$、R ∩ S、R ∪ S、R ◦ S也自反
  2. R，S反自反，$R^{-1}$、R ∩ S、R ∪ S、R - S也反自反
  3. R，S对称，$R^{-1}$、R ∩ S、R ∪ S、R - S也对称
  4. R，S反对称，$R^{-1}$、R ∩ S、R - S也反对称
  5. R，S传递，$R^{-1}$、R ∩ S也传递

• 闭包

  1. 定义：为使关系R满足所需要的性质，向R中尽可能少的添加元素，得到关系R’，使R’满足该性质，R’即为闭包。自反闭包记为r®，对称闭包记为s®，传递闭包记为t®。
  2. 用关系运算求闭包：
     • r® = R ∪ $I_A$
     • s® = R ∪ $R^{-1}$
     • t®利用上述收敛性公式求

4.4. 特殊关系

等价关系

• 等价关系：A上自反，对称，传递的关系。

• 等价类：设R为A上的一个等价关系，x∈R，则满足{y | y ∈ A ∧ xRy}的集合称为x的等价类，记为$[x{]}_R$，可简记为[x]。即x的等价类就是所有满足xRy的，y的集合。

• 等价类的性质：

  1. [x]非空
  2. 若xRy，则[x] = [y]；否则[x] ∩ [y] = ∅
  3. ∪{[x] | x ∈ A} = A

• 商集：{ $[x{]}_R$ | x ∈ A}，称为A关于R的商集，记作A / R。即A所有等价类的集合。

• 集合的划分：将集合的元素划分，商集就是对A的一个划分，也称由R导出的等价划分。
  一个集合有多种划分，不同等价关系导出不同的划分；且可由划分确定一个等价关系，假设有划分{S₁, S₂, …, $S_n$}，则对应的等价关系为{(S₁ × S₁) ∪ (S₂ × S)₂ ∪ … ∪ ($S_n\times S_n$)}。

偏序关系

• 偏序关系：A上自反，反对称，传递的关系R，记为≼，并将<a, b> ∈ ≼记为a ≼ b，<A, ≼>称为偏序集。该关系一般用于排序，因此是反对称的，典型的关系就是实数集上的小于等于关系。

• 可比：x ≼ y或y ≼ x则称x与y可比。

• 覆盖：当x ≼ y，且不存在z，使得x ≼ z ≼ y，则称y覆盖x。

• 哈斯图：本质就是采用一些规则化简关系图

  1. 取消每个点自环（因为自反性）
  2. 取消由传递性产生的边
  3. 重新排列每条边，使得箭头方向均朝上，然后去掉箭头（因为反对称性）

• 特殊元素：设<A, ≼>是偏序集，B是A的一个子集

  1. 最大元与最小元：∃b ∈ B，对∀x ∈ B，都有x ≼ b（b ≼ x），则称b为最大元（最小元）。

     必须与集合内其他元素都可比，且最大或最小。
     从哈斯图上看，单独的最高点（最低点）才是最大元（最小元）。

  2. 极大元与极小元：∃b ∈ B，对∀x ∈ B，不存在b ≺ x（x ≺ b），则称b为极大元（极小元）。

     在与其可比元素构成的集合内最大或最小。
     从哈斯图上看，只要处于子集的最高点（最低点），就都是极大元（极小元）。

  3. 上界与下界：∃a ∈ A，对∀x ∈ B，都有x ≼ a（a ≼ x），则称a为B的上界（下界）。a可以有多个。
  4. 上确界和下确界：上界（下界）的最小元（最大元），它们是唯一的。

• 拟序关系：A上反自反，反对称，传递的关系，用≺表示

• 全序关系：若偏序集<A, ≼>任意的x和y都可比，则称“≼”为全序关系，<A, ≼>为全序集，或线序集（因为哈斯图的元素排成一条线）

4.5. 函数

• 定义：设f是集合A到B的关系，且对∀x ∈ A，都存在惟一的y ∈ B，使得<x, y> ∈ f，则称f是A到B的函数，记为 f: A → B。

  定义域（原像）domf = A；值域（像）ranf = B。

• 函数的两个前提：domf中任意元素都有像；domf中同一元素有且仅有一个像。

• 关系与函数的区别：

  区别	种数	基数	第一元素
  关系	$2^{\Vert A\Vert \times \Vert B\Vert }$	0 ~ |A|×|B|	可重复
  函数	$\Vert B{\Vert }^{\Vert A\Vert }$	|A|	不可重复

• 特殊函数：

  1. 特征函数：设A为集合，对∀A’ ⊆ A，A’的特征函数 χ A ′ : A → { 0 , 1 } \chi_{A'}:A\to\{0,1\} χA′​:A→{ 0,1}定义为
     $${\chi }_{A^{\prime }}(a)=\{\begin{array}{l}1,a\in A^{\prime }\\ 0,a\in A-A^{\prime }\end{array}$$

• 函数类型：

  1. 单射：x与y一一对应；单射 ⇔ 对∀x₁，x₂ ∈ A，若x₁ ≠ x₂，则f(x₁) ≠ f(x₂)。
  2. 满射：ranf = B；满射 ⇔ 对∀y ∈ B，一定∃x ∈ A，使得f(x) = y。
  3. 双射：f单射且满射。

• 函数运算

  1. 复合：设有函数 f: A → B，g: B → C，则 f ◦ g: A → C。
     • f ◦ g(x) 也记为g(f(x))
     • dom(f ◦ g) = domf；ran(f ◦ g) = ranf
     • 复合运算不满足交换律，但满足结合律
     • 复合的保守性：相同类型的函数复合后还是同一类型
  2. 逆：$f^{-1}$: B → A
     • $f^{-1}$存在 ⇔ f是双射函数。（其实就是高数上的严格单调函数必有反函数）
     • $f◦f^{-1}=I_A$；$f^{-1}◦f=I_B$
  3. B上A：从A到B全体函数的集合，记为$B^A$

5. 图（G = <V, E>）

5.1. 概念

• 分类：有向图和无向图，多重图和线图（简单图是无环的线图），赋权图和无权图。

  环就是自环；圈是回路

• 各种图
  1. 零图：孤立结点组成的图。
  2. 平凡图：只有一个结点的零图。
  3. 子图：G₁ = <V₁, E₁>，V₁ ⊆ V，E₁ ⊆ E，则G₁为G的子图。
     • 生成子图：V₁ = V，E₁ ⊆ E
     • 导出子图：V₁ ⊆ V，E₁是以V₁中两个点为端点的边集
  4. 完全图：任意两点都有边相连，记为$K_n$（有向情况下为两条相反的边）。
  5. 补图：设简单图G = <V, E>，完全图G’ = <V, E₁>，则补图G₁ = <V, E₁ - E>。即从完全图的边集中删去简单图的边集。
  6. 同构图：若存在双射函数 f: V → V’，且对应边集相同，则称为同构图，记为G ≌ G’。

     简单而言就是一个图顶点挪动位置后形成的新图，都算同构图。文章来源地址https://www.toymoban.com/news/detail-400558.html

  7. 正则图：对∀v ∈ V，都有d(v) = k，则称G为 k-正则图。
  8. 竞赛图：为无向完全图的每条边分配方向所形成的图。
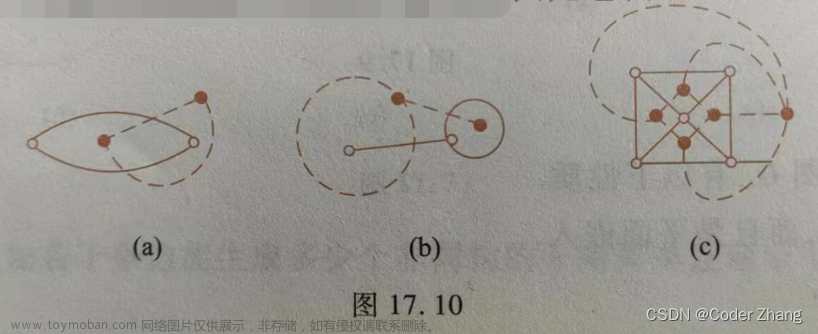
  9. 轮图：在n-1阶的圈内放置一个顶点，与各顶点相连，组成的就是n阶轮图，记为$W_n$
• 度：顶点的度记为d(v)，出度为 d + d^{+} d

到了这里，关于离散数学笔记整理（个人向）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！