1.numpy
主要用于高维的数组运算,拥有运算速度快的数学库;Numpy支持常见的数组和矩阵操作。Numpy使用ndarray对象来处理多维数组,该对象是一个快速而灵活的大数据容器。
安装
windows:
升级 pip:
python3 -m pip install -U pip
安装 Numpy库:(Ubuntu一样)
pip install numpy
下载完成后可以在Python文件中
import numpy print(numpy.__version__)来测试是否安装成功
2.ndarray
ndarray是一个n为数组,是相同类型的items的集合。使用ndarray的计算速度大于使用list,并且数组越大,ndarray的优势越大,所以为了节省时间使用ndarray进行存储数据。
import numpy as np
# 创建ndarray
# 一维数组
a = np.array([1,2,3,4])
# 二维数组
b = np.array([[1,2],[3,4]])
# 三位数组
c = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])
ndarray在存储数据的时候,因为ndarray中的所有元素的类型都是相同的,所以数据与数据的地址都是连续的,批量操作数组元素时速度更快。这是而Python列表中的元素类型是任意的,存储类似数据结构中的链表。在科学计算中,Numpy的ndarray就可以省掉很多循环语句,代码使用方面比Python原生list简单的多。numpy内置了并行运算功能(向量化运算),当系统有多个核心时,做某种计算时,numpy会自动做并行计算。
(1)ndarray属性
| 属性 | 含义 |
|---|---|
| ndarray.shape | 数组维度的元组 |
| ndarray.ndim | 数组维数 |
| ndarray.size | 数组中的元素数量 |
| ndarray.itemsize | 一个数组元素的长度(字节) |
| ndarray.dtype | 数组元素的类型 |
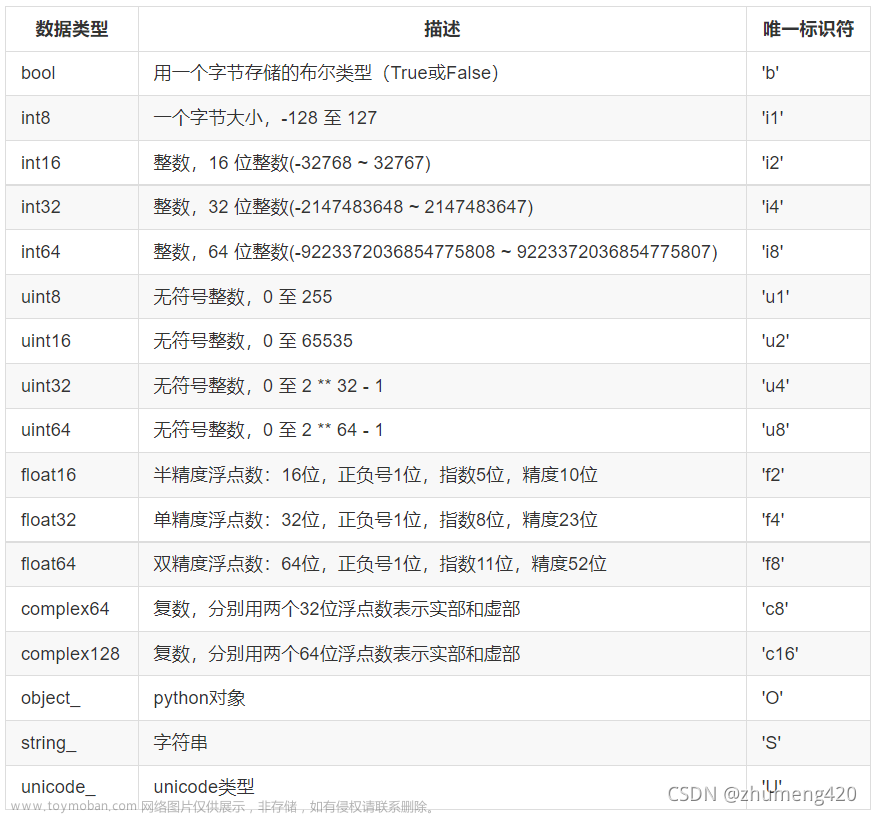
(2)ndarray类型
因为并不像python的列表一样可以存放不同类型的值,而是和c语言一样存放相同类型的值,所以在创建数组时就需要指定类型
a = np.array([[1,2],[3,4],[5,6]], dtype=np.int32)
a = np.array([['hello'],['world']], dtype=np.string_)
dtype参数是指定数组类型,若不指定则若数组中为整数时数组类型默认为int64,若数组中为小数时默认为float64
| 名称 | 描述 | 简写 |
|---|---|---|
| np.bool | 用一个字节存储的布尔类型(True或False) | ‘b’ |
| np.int8 | 一个字节大小,-128 至 127 | ‘i’ |
| np.int16 | 整数,-32768 至 32767 | ‘i2’ |
| np.int32 | 整数,-2^31 至 2^32 -1 | ‘i4’ |
| np.int64 | 整数,-2^63 至 2^63 - 1 | ‘i8’ |
| np.uint8 | 无符号整数,0 至 255 | ‘u’ |
| np.uint16 | 无符号整数,0 至 65535 | ‘u2’ |
| np.uint32 | 无符号整数,0 至 2^32 - 1 | ‘u4’ |
| np.uint64 | 无符号整数,0 至 2^64 - 1 | ‘u8’ |
| np.float16 | 半精度浮点数:16位,正负号1位,指数5位,精度10位 | ‘f2’ |
| np.float32 | 单精度浮点数:32位,正负号1位,指数8位,精度23位 | ‘f4’ |
| np.float64 | 双精度浮点数:64位,正负号1位,指数11位,精度52位 | ‘f8’ |
| np.complex64 | 复数,分别用两个32位浮点数表示实部和虚部 | ‘c8’ |
| np.complex128 | 复数,分别用两个64位浮点数表示实部和虚部 | ‘c16’ |
| np.object_ | python对象 | ‘O’ |
| np.string_ | 字符串 | ‘S’ |
| np.unicode_ | unicode类型 | ‘U’ |
3.生成数组
(1)生成全0或者全1数组
- np.ones(shape, dtype):生成全1的数组
- np.ones_like(a, dtype) :将数组a变为全1
- np.zeros(shape, dtype):生成全0的数组
- np.zeros_like(a, dtype) :将数组a变为全0
np.ones([2,3])
# array([[1., 1., 1.],
# [1., 1., 1.]])
np.zeros([2,3])
# array([[0., 0., 0.],
# [0., 0., 0.]])
a=[1,2,3,4]
np.zeros_like(a)
# array([0, 0, 0, 0])
b=np.ones([2,3])
np.zeros_like(b)
# array([[0., 0., 0.],
# [0., 0., 0.]])
(2)从现有数组生成
- np.array(object, dtype):从现有的数组当中创建
- np.asarray(a, dtype):相当于索引的形式,并没有真正的创建一个新的
a = np.array([[1,2,3],[4,5,6]])
a1 = np.array(a)
a2 = np.asarray(a)
print("a=",id(a))
print("a1=",id(a1))
print("a2=",id(a2))
# a= 1962211796784
# a1= 1962211788720
# a2= 1962211796784
(3)生成固定范围的数组
- np.linspace (start, stop, num, endpoint):创建等差数组 — 指定数量
- start:序列的起始值
- stop:序列的终止值
- num:要生成的等差数列数量,默认为50
- endpoint:序列中是否包含stop值,默认为ture
- np.arange(start,stop, step, dtype):创建等差数组 —指定步长
- step:步长,默认值为1
- np.logspace(start,stop, num,base,endpoint):创建等比数列
- num:要生成的等比数列数量,默认为50
- base:指定对数的底,默认为10
# 等差数列指定数量
a=np.linspace(1,10,5,endpoint=True)
# 等差数列指定步长
b=np.arange(1,10,3)
# 等比数列
c=np.logspace(start=0,stop=4,num=5,base=3)
print(a)
print(b)
print(c)
# [ 1. 3.25 5.5 7.75 10. ]
# [1 4 7]
# [ 1. 3. 9. 27. 81.]
(4)生成随机数组
需要导入np.random模块
- 简单随机数: 产生简单的随机数据,可以是任何维度
- 排列:将所给对象随机排列
- 分布:产生指定分布的数据,如高斯分布等
- 生成器:种随机数种子,根据同一种子产生的随机数是相同的
①正态分布
正态分布是一种概率分布。正态分布是具有两个参数μ和σ的连续型随机变量的分布,记作N(μ,σ )。在我们生活、生产还有科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述。
-
μ:服从正态分布的随机变量的均值,决定了其分布图像位置,当μ=0时其图像中心在坐标轴中心0点
-
σ:此随机变量的标准差,决定了分布图像的幅度,即是瘦高还是矮胖,越小越瘦高,越大越矮胖
当μ=0,σ=1时,称为标准正态分布
方差公式:σ^2

标准差:σ

正态分布创建
-
np.random.randn(d0, d1, …, dn)从标准正态分布中返回一个或多个样本值 ,参数为维度,即(2,3)为两行三列
-
np.random.normal(loc=0.0,scale=1.0, size=None):-
loc:μ此概率分布的均值(对应着整个分布的中心centre)
-
scale:σ此概率分布的标准差(对应于分布的宽度,scale越大越矮胖,scale越小,越瘦高)
-
size:输出样本数目,为int或元组(tuple)类型,例如,size=(m,n,k), 则输出
m*n*k个样本,缺省时输出1个值。
-
-
np.random.standard_normal(size=None)返回指定形状的标准正态分布的数组。
# 从标准正态分布中生成一个两行三列的数组
np.random.randn(2,3)
#array([[ 0.68407956, -0.88465943, 1.8113405 ],[-0.91357418, -0.98786321, 0.53993901]])
np.random.normal(0.0, 1, 5)
# array([-0.37305115, -0.47308456, 0.59911597, -0.35238895, 1.03690121])
np.random.standard_normal(size=5)
# array([ 1.20745242, 0.32335983, 1.01082709, -2.10252691, 0.60383283])
# 1.生成均匀分布的随机数
x1 = np.random.normal(1.75, 1, 100000000)
x2 = np.random.normal(-2, 0.5, 100000000)
# 创建一个标准正态分布进行比对
y= np.random.normal(0, 1, 100000000)
# 2.创建画布
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,5),dpi=100)
# 3.绘制直方图
axes[0].hist(x1, 1000)
axes[0].hist(y, 1000,color='r')
axes[1].hist(x2, 1000)
axes[1].hist(y, 1000,color='r')
# 4.图像保存不变
plt.savefig("./images/正态分布test1.png")
# 3)显示图像
plt.show()

③均匀分布
-
np.random.rand(d0, d1, ..., dn)- 返回**[0.0,1.0)**内的一组均匀分布的数。
-
np.random.uniform(low=0.0, high=1.0, size=None)-
功能:从一个均匀分布**[low,high)中随机采样,注意定义域是左闭右开**,即包含low,不包含high. 并且指的是x轴
-
low: 采样下界,float类型,默认值为0; -
high: 采样上界,float类型,默认值为1; -
size:输出样本数目,为int或元组(tuple)类型,例如,size=(m,n,k), 则输出
m*n*k个样本,缺省时输出1个值。 -
返回值:ndarray类型,其形状和参数size中描述一致。
-
-
np.random.randint(low, high=None, size=None, dtype='l')-
low: int生成的数值最低要大于等于low。(hign = None时,生成的数值要在[0, low)区间内)
-
high: int (可选)如果使用这个值,则生成的数值在[low, high)区间。
-
size:
输出样本数目,为int或元组(tuple)类型,例如,size=(m,n,k), 则输出m*n*k个样本,缺省时输出1个值。
-
np.random.randint(500,1000, size=10)
# array([664, 612, 887, 687, 987, 808, 776, 772, 635, 860])
np.random.uniform(-1, 1, 5)
# array([-0.6000072 , 0.15313873,-0.59614837, 0.17145161, 0.97448999)
import matplotlib.pyplot as plt
# 生成均匀分布的随机数
x1 = np.random.uniform(-1, 1, 100000)
x2 = np.random.randint(500,1000, size=100000)
# 2.创建画布
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,5),dpi=100)
# 3.绘制直方图
axes[0].hist(x1, 1000)
# axes[0].hist(y, 1000,color='r')
axes[1].hist(x2, 1000)
# axes[1].hist(y, 1000,color='r')
# 4.图像保存不变
plt.savefig("./images/正态分布test1.png")
# 3)显示图像
plt.show()

4.数组索引、切片
# 三维数组
a = np.array([[[1,2,3],[4,5,6]], [[7,8,9],[10,11,12]]])
# 1.索引,按维度,第2行第1列
print("a[1,0]=",a[1,0])
# a[1,0]= [7 8 9]
# 2.切片,第1行到第2行
print("a[1:3]=",a[1:3])
# a[1:3]= [[[ 7 8 9]
# [10 11 12]]]
# 3.索引和切片结合,第1行到第2行的第2列
print("a[0:2,1]=",a[0:2,1])
# a[0:2,1]= [[ 4 5 6]
# [10 11 12]]
# 4.索引和切片结合,第1行到第2行的第1列到第2列
print("a[0:2,0:2]=",a[0:2,0:2])
# a[0:2,0:2]= [[[ 1 2 3]
# [ 4 5 6]]
# [[ 7 8 9]
# [10 11 12]]]
5.数组形状改变
-
对象.reshape()- 没有进行行列互换,新产生一个ndarray
a = np.array([[1,2],[3,4]])
b = a.reshape([1,4])
# a=array([[1,2],[3,4]])
# b=array([[1,2,3,4]])
-
对象.resize()- 没有进行行列互换,修改数组本身的形状(需要保持元素个数前后相同)
a = np.array([[1,2,3],[4,5,6]])
a.resize([3,2])
a
# array([[1, 2],
# [3, 4],
# [5, 6]])
a = np.array([[1,2],[3,4]])
a.resize([1,4])
a
# array([[1, 2, 3, 4]])
-
对象.T- 进行了行列互换
a = np.array([1,2,3],[4,5,6])
a.T
# array([[1, 4],
# [2, 5],
# [3, 6]])
# 查看数组维度
a.shape
# (2, 3)即2行3列
a.T.shape
# (3, 2)即3行2列
6.数组合并去重
即将数组所有元素进行合并并去重
a=np.array([[1,2],[2,3],[3,4]])
np.unique(a)
# array([1, 2, 3, 4])
7.ndarray运算
(1)逻辑运算
- 直接进行大于,小于的判断
- 合适之后,可以直接进行赋值
a=np.array([1,3,5,7,9,2,4,6,8])
# 逻辑判断,判断是否大于5
a>5
# array([False, False, False, True, True, False, False, True, True])
# BOOL赋值, 将满足条件的设置为指定的值-布尔索引
a[a>5]=0
a
# array([1, 3, 5, 0, 0, 2, 4, 0, 0])
(2)判断函数
-
np.all():判断所有元素是否成立
-
np.any():判断是否有任意元素成立
a=np.array([1,3,5,7,9,2,4,6,8])
np.all(a>5)
# False
np.any(a>5)
# True
(3)三元运算np.where
当遇到复杂的运算时,可以使用np.where进行运算。复合逻辑需要结合np.logical_and和np.logical_or使用
a=np.array([1,3,5,7,9,2,4,6,8])
# 1.判断所有元素是否大于5,若大于则设置为1,否则设置为0
np.where(a>5,1,0)
# array([0, 0, 0, 1, 1, 0, 0, 1, 1])
# 2.判断所有元素是否大于5并且小于7,若成立则设置为1,否则设置为0
np.where(np.logical_and(a>5,a<7),1,0)
# array([0, 0, 0, 0, 0, 0, 0, 1, 0])
# 3.判断所有元素是否小于5或大于7,若成立则设置为1,否则设置为0
np.where(np.logical_or(a<5,a>7),1,0)
array([1, 1, 0, 0, 1, 1, 1, 0, 1])
(4)统计运算
-
np.max():最大值 -
np.min():最小值 -
np.median():中位数 -
np.mean():算术平均值 -
np.std():标准差是一组数据平均值分散程度的一种度量。 -
np.var():方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数,即mean((x - x.mean())** 2)。 -
np.ptp():计算数组中元素最大值与最小值的差(最大值 - 最小值)。 -
np.argmax(axis=): 最大元素对应的下标 -
np.argmin(axis=):最小元素对应的下标
8.数组与数,数组与数组
a=[1,2]
a+1
# 报错,因为列表只能连接列表
a=np.array([1,2])
a+1
# [2,3] # 是值的相加
a=[1,2]
b=[2]
a+b
# [1, 2, 2] # 是数组(列表)的拼接
a=np.array([1,2])
b=np.array([2])
a+b
# array([3, 4]) # 是值的相加
a=np.array([1,2])
b=np.array([2,3])
a+b
# array([3, 5]) # 是值的相加
NumPy 广播(Broadcast)
在np.array数组中,当参与运算的数组形状(shape)不同时,会将它们进行扩展,使得shape相同,再进行运算。
如下图:

9.线性代数
NumPy 提供了线性代数函数库 linalg,该库包含了线性代数所需的所有功能
| 函数 | 描述 |
|---|---|
dot |
两个数组的点积,即元素对应相乘。 |
vdot |
两个向量的点积 |
inner |
两个数组的内积 |
matmul |
两个数组的矩阵积 |
determinant |
数组的行列式 |
solve |
求解线性矩阵方程 |
inv |
计算矩阵的乘法逆矩阵 |
a=np.array([[1,2],[3,4]])
b=np.array([2,2])
np.dot(a,b)
# array([ 6, 14])
np.matmul(a,b)
# array([ 6, 14])
注意:二者都是矩阵乘法。 np.matmul中禁止矩阵与标量的乘法。 在矢量乘矢量的內积运算中,np.matmul与np.dot没有区别。
,即元素对应相乘。 |
|vdot| 两个向量的点积 |
|inner| 两个数组的内积 |
|matmul| 两个数组的矩阵积 |
|determinant| 数组的行列式 |
|solve| 求解线性矩阵方程 |
|inv| 计算矩阵的乘法逆矩阵 |文章来源:https://www.toymoban.com/news/detail-400631.html
a=np.array([[1,2],[3,4]])
b=np.array([2,2])
np.dot(a,b)
# array([ 6, 14])
np.matmul(a,b)
# array([ 6, 14])
注意:二者都是矩阵乘法。 np.matmul中禁止矩阵与标量的乘法。 在矢量乘矢量的內积运算中,np.matmul与np.dot没有区别。文章来源地址https://www.toymoban.com/news/detail-400631.html
到了这里,关于Numpy数组和矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!

![系统学习Numpy(一)——numpy的安装与基础入门[向量、矩阵]](https://imgs.yssmx.com/Uploads/2024/02/594520-1.png)