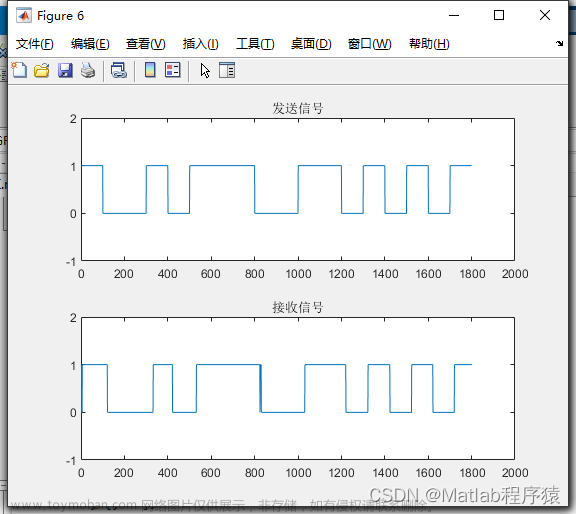
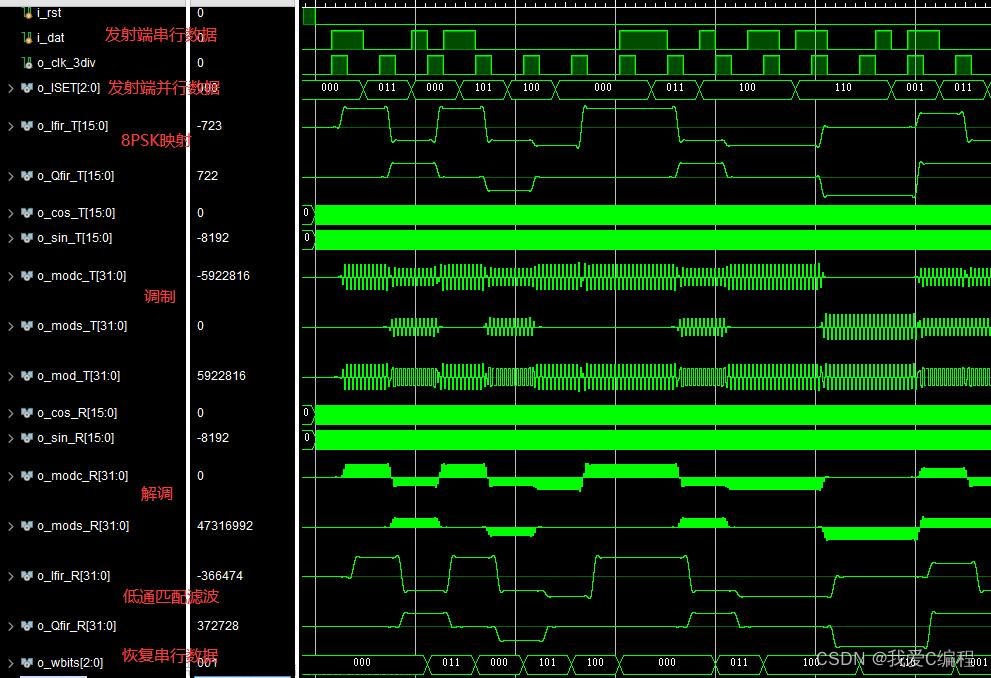
一、代码解析
使用audioread读取音频信号，将采样率设置为100kHz，并利用awgn函数为信号添加高斯白噪声。
%% 读取信号添加高斯白噪声并播放
fs1=1e5; %设定采样率为100kHz
[x1,fs] = audioread('xiaomi1.wav'); % 输入第一路信号
x1=resample(x1,fs1,fs); %对采样率进行调整
fs=fs1;
snr=20; % 设置告诉白噪声与信号的信噪比
px_dBW=0; %信号指定功率
x1=awgn(x1,snr,px_dBW); % 调用awgn函数为信号添加高斯白噪声
[x2,fs] = audioread('xiaomi2.wav');
x2=x2*4; %对第二段音频本身响度低，响度进行增强
x2=resample(x2,fs1,fs);
fs=fs1;
x2=awgn(x2,snr,px_dBW);
分别绘制两路音频信号的时频域图。
%% 绘制信号时域和频域图
figure(1);
subplot(221);
N1=length(x1);
N2=length(x2);
N=max(N1,N2); %取两路信号中较长的那路长度作为下面信号操纵的长度，保证信号长度一致
x1=[x1;zeros(N-N1,1)]; %对较短的信号进行补零
x2=[x2;zeros(N-N2,1)];
t=(0:N-1)/fs;% 计算时间坐标
plot(t,x1);
xlabel("时间");
ylabel("幅度");
title("第一路信号时域图");
subplot(223);
y=abs(fftshift(fft(x1))); %快速傅里叶变换的幅值
f=(0:N-1)*fs/N-fs/2; %将横坐标转化，并对齐零点，显示为频率f
plot(f,y);
xlabel('频率');
ylabel('幅度');
title("第一路信号频域图");
subplot(222);
plot(t,x2);
xlabel("时间");
ylabel("幅度");
title("第二路信号时域图");
subplot(224);
y=abs(fftshift(fft(x2))); %快速傅里叶变换的幅值
plot(f,y);
xlabel('频率');
ylabel('幅度');
title("第二路信号频域图");
结果如下：
设置两路不同频率的载波，这里设置频率分别为35kHz和25kHz，载波频率可以根据需要进行更改，但是注意需要满足奈奎斯特采样定理，即信号频率不能超过采样频率的1/2，我们在开始设置了采样频率为100kHz，所以我们整个操作过程中所有频率的信号都不能大于50kHz。
%% 配置载波
f1=3.5e4; %第一路载波
y1=sin(2*pi*f1*t);
f2=2.5e4; %第二路载波
y2=sin(2*pi*f2*t);
对音频信号进行AM调制，并显示调制后信号的时频域图。
%% 用AM调制方式将信号分别叠加到载波上
x1=x1+1;
z1=x1.*y1';
figure(2);
subplot(221);
plot(t,z1);
xlabel("时间");
ylabel("幅度");
title("第一路信号与载波叠加的时域图");
subplot(223);
y = abs(fftshift(fft(z1))); %快速傅里叶变换的幅值
plot(f,y);
xlabel('频率');
ylabel('幅度');
title("第一路信号与载波叠加的频域图");
x2=x2+1;
z2=x2.*y2';
subplot(222);
plot(t,z2);
xlabel("时间");
ylabel("幅度");
title("第二路信号与载波叠加的时域图");
subplot(224);
y = abs(fftshift(fft(z2))); %快速傅里叶变换的幅值
plot(f,y);
xlabel('频率');
ylabel('幅度');
title("第二路信号与载波叠加的频域图");
结果如下：
两路信号在空间中直接进行混叠。
%% 信号在空间中叠加
z=z1+z2;
接收到信号后，利用滤波器滤出两路载波，这里设置截止频率均为30kHz的切比雪夫二型滤波器，分别为低通和高通。滤波器函数生成方法见后文。
%% 信号分离
z1=filter(Chebyshev_two_high_15_100000_30000,z); %以30kHz为界，分开两路信号
z2=filter(Chebyshev_two_low_15_100000_30000,z);
对滤出的两路信号分别进行相干解调，因为经过了调制和解调后，信号的幅度和中心点会发生偏移，这里进行调整，将信号中心重新放回0上，并将最大幅度调整为1，即与最开始输入的音频信号保持一致。
相干解调后，信号频谱再次搬移，会得到分别得到中心频率为0和2倍载波频率的共3路信号，使用低筒滤波器滤除载波信号，仅保留中心频率为0的信号（即为需要的音频信号）。使用低通滤波器依然为切比雪夫二型。并绘制最终解调恢复的两路音频信号的时频域图。
%% 相干解调
r1=z1.*y1'; %对第一路信号使用相干解调方法进行解调
r1=2*(r1-0.5); %中心回归零位并调整与原信号幅度一致
r1=filter(Chebyshev_two_low_10_100000_20000,r1); %设计切比雪夫二型低通滤波器进行滤波，滤除载波信号，保留音频信号
figure(3);
subplot(221);
plot(t,r1);
xlabel("时间");
ylabel("幅度");
title("解调出的第一路音频时域图");
subplot(223);
z = abs(fftshift(fft(r1))); %快速傅里叶变换的幅值
plot(f,z);
xlabel('频率');
ylabel('幅度');
title("解调出的第一路音频频域图");
r2=z2.*y2'; %对第二路信号使用相干解调方法进行解调
r2=2*(r2-0.5); %中心回归零位并调整与原信号幅度一致
r2=filter(Chebyshev_two_low_10_100000_20000,r2); %设计切比雪夫二型低通滤波器进行滤波，滤除载波信号
subplot(222);
plot(t,r2);
xlabel("时间");
ylabel("幅度");
title("解调出的第二路音频时域图");
subplot(224);
z = abs(fftshift(fft(r2))); %快速傅里叶变换的幅值
plot(f,z);
xlabel('频率');
ylabel('幅度');
title("解调出的第二路音频频域图");
结果如下：
结尾设置对解调音频的播放，可以用以比较解调出的音频信号与原始音频信号。
%% 暂停等待播发，按任意键结束程序
sound(r1,fs); %播放解调出的第一路音频
pause;
clear sound
sound(r2,fs); %播放解调出的第二路音频
pause;
clear all
二、滤波器的设置
可以在命令行输入fdatool打开，也可以从下面的方法进入。
进入matlab，选择APP，注意这里的路径需要为matlab安装目录下的bin文件夹，不然有可能报错。
在APP下拉菜单里面找到“信号处理与通信”里面的“Filter Designer”，点击打开
打开后在如下图所示的界面中第一栏可以选择滤波器类型（低通、高通、带通等）以及滤波方法（巴特沃斯、切比雪夫、椭圆等），每种滤波方法特性不一样。第二栏指定滤波的阶数，可以指定也可以采用系统给出的最小阶数。第三栏设置采样频率和截止频率。第四栏一般不管。
如下图设置为低通、切比雪夫二型、15阶、采样48000Hz、截止12000Hz的滤波器，选定参数后，点击最下方的Design Filter可以显示当前滤波器的特性曲线，点击上方状态栏的不同图标可以更换去向类型。
将滤波器导出为函数，点击左上角File按钮，如下图选择，即可导出.m格式的Function文件，保存到同一文件夹下，就可以进行调用。使用filter函数调用，示例如下：
z1=filter(Chebyshev_two_high_15_100000_30000,z); %以30kHz为界，分开两路信号
文章来源：https://www.toymoban.com/news/detail-400806.html
完整代码分享
双路音频信号的AM调制与解调文章来源地址https://www.toymoban.com/news/detail-400806.html
到了这里，关于基于matlab实现双路音频信号的AM调制与解调的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
