奇异值分解(SVD)和np.linalg.svd()函数用法-Toy模板网

这篇具有很好参考价值的文章主要介绍了奇异值分解(SVD)和np.linalg.svd()函数用法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、简介

奇异值分解是一种十分重要但又难以理解的矩阵处理技术，在机器学习中是最重要的分解没有之一的存在。那么，奇异值分解到底是在干什么呢？

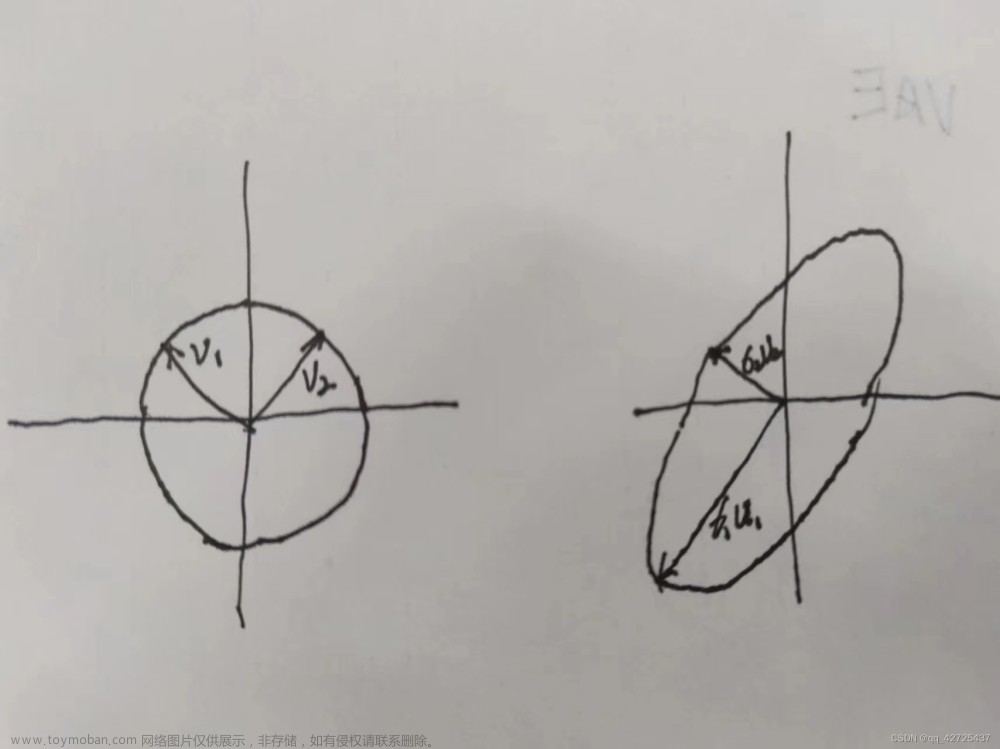
矩阵 A 表示的是高维数据，通常情况下高维数据分布并不是雨露均沾的，而往往是厚此薄彼，集中分布在某些维度上，如下图

奇异值分解(SVD)和np.linalg.svd()函数用法

虽然原始数据的的确确是二维数据，但是其实主要集中分布在直线 L (一维空间)附近，在这里，SVD(奇异值分解)其实就是在寻找直线 L ，然后将数据映射到直线 L 上，实现数据降维的过程，即如下图

奇异值分解(SVD)和np.linalg.svd()函数用法

于是，通过SVD(奇异值分解)，就可以利用降维后的数据近似地替代原始数据。所以，SVD(奇异值分解)其实就是在寻找数据分布的主要维度，将原始的高维数据映射到低维子空间中实现数据降维。

二、概念

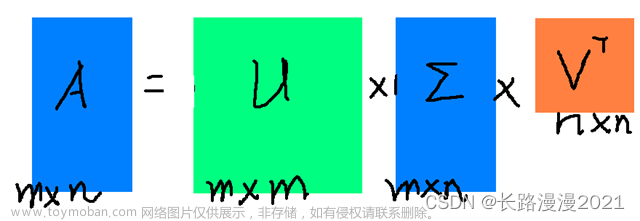
奇异值分解（singular Value Decomposition），简称SVD，线性代数中矩阵分解的方法。假如有一个矩阵A，对它进行奇异值分解，可以得到三个矩阵：

矩阵除了对角元素不为0，其他元素都为0，并且对角元素是从大到小排列的，前面的元素比较大，后面的很多元素接近0。这些对角元素就是奇异值。

中有n个奇异值，但是由于排在后面的很多接近0，所以我们可以仅保留比较大的r个奇异值：

实际应用中，我们仅需保留着三个比较小的矩阵，就能表示A，不仅节省存储量，在计算的时候更是减少了计算量。SVD在信息检索（隐性语义索引）、图像压缩、推荐系统、金融等领域都有应用。

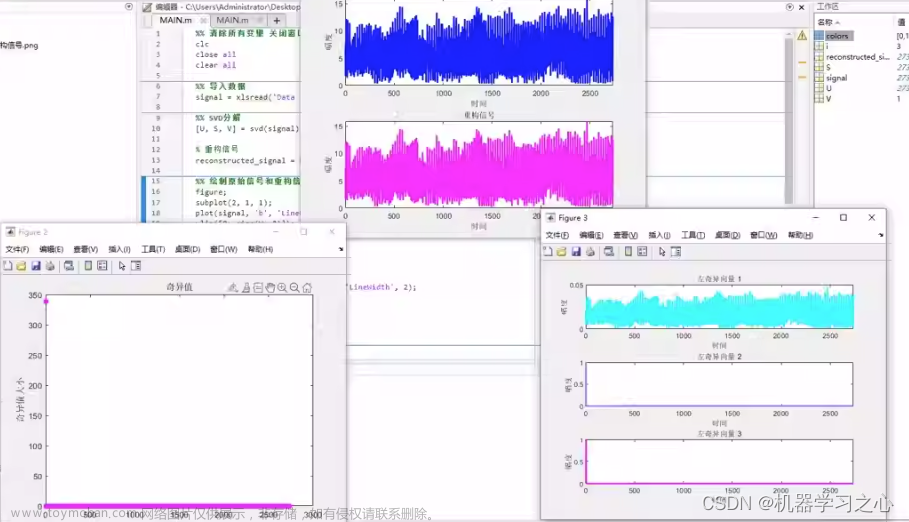
SVD一个重要的应用就是图像压缩存储，因为数字图像本身就是个矩阵，通过一个近似的低秩矩阵替代原矩阵，可以大大减少存储量。SVD还有很多用途，比如机器学习中的主成分分析，这才是直接利用低维矩阵 M 替代原矩阵 A 实现降维。

三、np.linalg.svd(a,full_matrices=1,compute_uv=1)用法描述

参数：
a是一个形如(M,N)矩阵

full_matrices的取值是为0或者1，默认值为1，这时u的大小为(M,M)，v的大小为(N,N) 。否则u的大小为(M,K)，v的大小为(K,N) ，K=min(M,N)。

compute_uv的取值是为0或者1，默认值为1，表示计算u,s,v。为0的时候只计算s。

返回值：

总共有三个返回值u,s,v
u大小为(M,M)，s大小为(M,N)，v大小为(N,N)。

A = u*s*v

其中s是对矩阵a的奇异值分解。s除了对角元素不为0，其他元素都为0，并且对角元素从大到小排列。s中有n个奇异值，一般排在后面的比较接近0，所以仅保留比较大的r个奇异值。

例子：

>>> from numpy import *
>>> data = mat([[1,2,3],[4,5,6]])
>>> U,sigma,VT = np.linalg.svd(data)
>>> print U
[[-0.3863177  -0.92236578]
 [-0.92236578  0.3863177 ]]
>>> print sigma
[9.508032   0.77286964]
>>> print VT
[[-0.42866713 -0.56630692 -0.7039467 ]
 [ 0.80596391  0.11238241 -0.58119908]
 [ 0.40824829 -0.81649658  0.40824829]]

因为sigma是除了对角元素不为0，其他元素都为0。所以返回的时候，作为一维矩阵返回。本来sigma应该是由3个值的，但是因为最后一个值为0，所以直接省略了。

四、例子

>>> a = np.random.randn(9, 6) + 1j*np.random.randn(9, 6)
>>> b = np.random.randn(2, 7, 8, 3) + 1j*np.random.randn(2, 7, 8, 3)

基于全 SVD 的重构，2D 案例：

>>> u, s, vh = np.linalg.svd(a, full_matrices=True)
>>> u.shape, s.shape, vh.shape
((9, 9), (6,), (6, 6))
# numpy的allclose方法，比较两个array是不是每一元素都相等，默认在1e-05的误差范围内
>>> np.allclose(a, np.dot(u[:, :6] * s, vh))
True

>>> smat = np.zeros((9, 6), dtype=complex)
>>> smat[:6, :6] = np.diag(s)
>>> np.allclose(a, np.dot(u, np.dot(smat, vh)))
True

基于简化 SVD 的重建，2D 案例：

>>> u, s, vh = np.linalg.svd(a, full_matrices=False)
>>> u.shape, s.shape, vh.shape
((9, 6), (6,), (6, 6))
>>> np.allclose(a, np.dot(u * s, vh))
True
>>> smat = np.diag(s)
>>> np.allclose(a, np.dot(u, np.dot(smat, vh)))
True

基于全SVD、4D案例的重构：

>>> u, s, vh = np.linalg.svd(b, full_matrices=True)
>>> u.shape, s.shape, vh.shape
((2, 7, 8, 8), (2, 7, 3), (2, 7, 3, 3))
>>> np.allclose(b, np.matmul(u[..., :3] * s[..., None, :], vh))
True
>>> np.allclose(b, np.matmul(u[..., :3], s[..., None] * vh))
True

基于简化 SVD 的重建，4D 案例：

>>> u, s, vh = np.linalg.svd(b, full_matrices=False)
>>> u.shape, s.shape, vh.shape
((2, 7, 8, 3), (2, 7, 3), (2, 7, 3, 3))
>>> np.allclose(b, np.matmul(u * s[..., None, :], vh))
True
>>> np.allclose(b, np.matmul(u, s[..., None] * vh))
True