Java系列文章目录

Write once,Runanywhere.🔥🔥🔥
本派文章详细斐波那契数列、青蛙跳台阶、汉诺塔(C语言Java通用)、递归练习题。
💥 💥 💥如果你觉得我的文章有帮助到你,还请【关注➕点赞➕收藏】,得到你们支持就是我最大的动力!!!
💥 💥 💥
⚡版权声明:本文由【马上回来了】原创、在CSDN首发、需要转载请联系博主。
版权声明:本文为CSDN博主「马上回来了」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。

🚀🚀🚀 新的知识开始喽🚀🚀🚀
1.斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)。
1.1 递归实现斐波那契数列
//递归实现斐波那契数列
//1 1 2 3 5 8 13 21 34 55 89
public static void main(String[] args) {
int n = 11;//求第十一个斐波那契数
int ret = fabonacci(n);
System.out.println(ret);
}
public static int fabonacci(int n){
if(n==1 || n==2){//递归的初始条件
return 1;
}else {
return fabonacci(n-1)+fabonacci(n-2);//递归的递推公式
}
}
但是用递归来实现斐波那契数列并不高效,因为计算n时每一个数字都要往前递推,看下面代码:
//递归实现斐波那契数列
//1 1 2 3 5 8 13 21 34 55 89
public static void main(String[] args) {
int n = 39;//求第39个斐波那契数
int ret = fabonacci(n);
System.out.println(ret);
System.out.println("n = 3被计算的次数:"+count);
}
public static int count = 0;
public static int fabonacci(int n){
if(n==1 || n==2){
return 1;
}else {
if(n == 3){
count++;
}
return fabonacci(n-1)+fabonacci(n-2);
}
}
}

1.2 循环实现斐波那契数列
上面的代码在计算第39个斐波那契数时,n=3被计算了太多次,效率不高,因此我们一般用循环(迭代)来实现斐波那契数列,看下面代码:
//循环实现斐波那契数列
// 1 1 2 3 5 8 13 21 34 55 89
public static void main(String[] args) {
int f1 = 1;
int f2 = 1;
int fn = 0;
Scanner in = new Scanner(System.in);
int n = in.nextInt();//输入n=8
while (n>2){
fn = f1+f2;
f1 = f2;
f2 = fn;
n--;
}
System.out.println(fn);
}

2.青蛙跳台阶

2.1问题叙述
青蛙每次跳台阶都有两种方式,一步跳一阶楼梯,一步跳两阶楼梯,问现在有n阶楼梯,青蛙跳完这n阶楼梯有几种方法?
2.2 .问题分析
当n=1时,一步跳一阶只有1种跳。
当n=2时,可以一步先只跳一阶,还剩下一阶,则剩下的跳法就是剩下这一个台阶的跳法;或者直接一步跳两阶,因此只有2种跳法。
当n=3时,先第一步跳一阶,还剩两阶,因此把这个台阶跳完的方法取决于这剩下的两个阶的跳法,也就是n=2的跳法,因此第一步跳一阶的跳法有2种;然后第一步跳两阶,还剩下一阶,也就是还剩下n=1的台阶的跳法,因此第一步跳两阶的跳法只有一种,总共有3中跳法。
当n=4时,第一步先跳一阶,还剩下三阶,把这个台阶跳完的方法取决于剩下的这三个台阶即n=3的跳法;第一步跳两阶,还剩下两阶即n=2的跳法,所以总的跳法=(n=2)+(n=3)=5种。
当n=5时,以此类推。
我们可以得出以下规律:
| 台阶数n | 跳法f |
|---|---|
| 1 | f(1)=1 |
| 2 | f(2)=2 |
| 3 | f(3)=f(3-1)(第一步跳一阶,剩下两阶)+f(3-2)(第一步跳l两阶,剩下一阶)=1+2=3 |
| 4 | f(4)=f(4-1)+f(4-2)=f(3)+f(2)=3+2=5 |
| n | f(n-1)+f(n-2) |
通过对结果的观察不能发现其实青蛙跳台阶问题就是一个斐波那契数列,因此代码实现斐波那契数列一样。
2.3 青蛙跳台阶进阶
现在青蛙每一步有三种跳法:
1.一步一阶
2.一步两阶
3.一步三阶
求青蛙跳n阶台阶有几种跳法?
分析:
n=1时,一步一阶1种;
n=2时,先一步一阶,还剩一阶,因此有1种跳法;先一步两阶,跳完,2种;
n=3时,先一步一阶,还剩两阶,剩下的两阶的跳法总数,就是第一步只跳一阶跳完整个台阶的方法,n=2有2种;先一步两阶,还剩一阶,n=1有1种;直接一步阶,跳完,有4种。
n=4时,以此类推,先一步一阶,还剩三阶,n=3有4种;先一步两阶,还剩两阶,n=2有2种;先一步三阶,n=1有1种,总共有4+2+1=7种。
n=5……
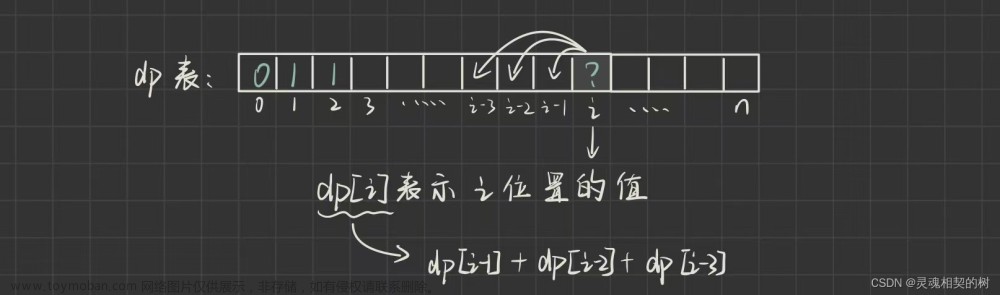
通过观察可以得出递推公式:
n<=3时,f(1) = 1,f(2) = 2,f(3)=4
n>3时,f(n)=f(n-1)+f(n-2)+f(n-3)
与原斐波那契数列相比,这里变成了从第四个数开始,每一位等于前面的三个数之和。原因在于增加了n=3时的初始条件。
1 2 4 7 13……
所以在弄懂了上面的原理之后,现在又给你出一道题:
现在青蛙每一步有k种跳法:
1.一步一阶
2.一步两阶
3.一步三阶
……
k.一步k阶
求青蛙跳n阶台阶有几种跳法?
我们很快就能得出,只是将初始条件由n=3改成了n=k,所以很快就能得出递推公式:
n<=k时,f(1) = 1,f(2) = 2,f(3)=4,……f(k)=假设K种
n>k时,f(n)=f(n-1)+f(n-2)+f(n-3)+……+f(n-k)
3.汉诺塔
汉诺塔C语言实现
之前我已经讲解过了C语言实现汉诺塔,可以点进去观看一下。
关键在于:
将每次都将n个盘子看做(n-1)+1,然后将(n-1)个盘子移到中间柱子y上,然后将剩下的一个盘子移到目标柱子z上,然后又将在y柱上的(n-1)个盘子又看做是(n-2)+1,将(n-2)个盘子移到中间柱子x上,然后将剩下的1个盘移到目标柱z上,以此类推,直到n=1为止。。代码让人难理解的地方就是因为,起始柱,中间柱,目标柱在每次递归的时候都在发生变化。
这里再用java实现一遍,看代码:
//汉诺塔
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();//输入你要移动的盘子数 n=3
hanoi(n,'X','Y','Z');
}
//移动
public static void move(char pos1,char pos2){
System.out.println(pos1+"->"+pos2);
}
public static void hanoi(int n,char pos1,char pos2,char pos3){
if(n==1){//只有1个盘子
move(pos1,pos3);//直接x->z
}else{
hanoi(n-1,pos1,pos3,pos2);//将n-1个盘子借助Z移到Y上
move(pos1,pos3);//将剩下的1个盘子从X移到Z上
hanoi(n-1,pos2,pos1,pos3);//将Y上的n-1个盘子再移到Z上
}
}
运行结果:
4 递归练习题
4.1按顺序打印一个数字的每一位(例如 1234 打印出 1 2 3 4) (递归)
//写一个递归方法,输入一个非负整数,返回组成它的数字之和
// 1921
public static void main(String[] args) {
int year = 1921;
print(year);
}
public static void print(int n){
if(n < 10){
System.out.print(n+" ");
}else{
print(n/10);
System.out.print(n%10+" ");
}
}

4.2 写一个递归方法,输入一个非负整数,返回组成它的数字之和
//写一个递归方法,输入一个非负整数,返回组成它的数字之和
// 1234=1+2+3+4=10
public static void main(String[] args) {
int n = 1234;
int ret = seadd(n);
System.out.println(ret);
}
public static int seadd(int n){
if(n<10){//起始条件
return n;//直接返回n的值
}else{
return n%10+seadd(n/10);//递推公式 假设n=12 则这里返回的值:12%10+1=3
}
}

4.3 递归求 1 + 2 + 3 + … + 10
//递归求 1 + 2 + 3 + ... + 10
public static void main(String[] args) {
int n = 10;
int ret = add(n);
System.out.println(ret);
}
public static int add(int n){
if(n==1){//起始条件
return 1;
}else{
return n+add(n-1);//递推公式 当n=2时,return 2+1 =3
}
}

4. 4递归求 N 的阶乘
//递归求 N 的阶乘
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();//输入你要求的阶乘 n=5
int ret = fac(n);
System.out.println(ret);
}
public static int fac(int n){
if(n == 1){//初始条件
return 1;
}else {
return n*fac(n-1);//递推公式:当n=2时,return: 2*1=2
}
}

🌏🌏🌏今天的你看懂这里又学到了很多东西吧🌏🌏🌏文章来源:https://www.toymoban.com/news/detail-401254.html

🌔 🌔 🌔下次见喽🌔 🌔 🌔 文章来源地址https://www.toymoban.com/news/detail-401254.html
文章来源地址https://www.toymoban.com/news/detail-401254.html
到了这里,关于斐波那契数列、青蛙跳台阶、汉诺塔(C语言Java通用)、递归练习题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!