数据结构（Java）最小生成树（普里姆、克鲁斯卡尔算法）-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构（Java）最小生成树（普里姆、克鲁斯卡尔算法）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、概念

最小生成树(Minimum Cost Spanning Tree)，简称MST。

1) 给定一个带权的无向连通图 , 如何选取一棵生成树 , 使树上所有 边上权的总和为最小 ,就叫最小生成树

2) N 个顶点，一定有 N-1 条边

3) 包含全部顶点

4) N-1 条边都在图中

（好像不能形成闭合回路）

数据结构（Java）最小生成树（普里姆、克鲁斯卡尔算法）

求最小生成树的算法主要是普里姆算法和克鲁斯卡尔算法

二、普里姆算法Prim

1) 普利姆 (Prim) 算法求最小生成树，也就是在包含 n 个顶点的连通图中，找出只有 (n-1) 条边包含所有 n 个顶点的连通子图，也就是所谓的 极小连通子图

2) 普利姆的算法思路如下 :

(1) 设 G=(V,E) 是连通网， T=(U,D) 是最小生成树， V,U 是顶点集合， E,D 是边的集合

(2) 若从顶点 u 开始构造最小生成树，则从集合 V 中取出顶点 u 放入集合 U 中，标记顶点 v的visited[u]=1

(3) 若集合 U 中顶点 ui 与集合 V-U 中的顶点 vj 之间存在边，则寻找这些边中权值最小的边，但不能构成回路，将顶点 vj 加入集合 U 中，将边（ ui,vj ）加入集合 D 中，标记 visited[ vj ]=1

(4) 重复步骤②，直到 U 与 V 相等，即所有顶点都被标记为访问过，此时 D 中有 n-1 条边

我们直接用案例来理解这个算法。

修路问题：

数据结构（Java）最小生成树（普里姆、克鲁斯卡尔算法）

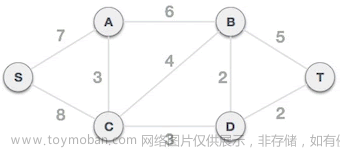
1)有胜利乡有7个村庄(A, B, C, D, E, F, G) ，现在需要修路把7个村庄连通

2) 各个村庄的距离用边线表示 ( 权 ) ，比如 A – B 距离 5 公里

3) 问：如何修路保证各个村庄都能连通，并且总的修建公路总里程最短 ?

prim算法的解析：

比如我们从G点出发，标记已访问，用temp变量存储已访问的顶点，

temp.add(G) -> {G}

首先找出与G邻接且二者间权最小并且未被访问的点，也就是 A，

temp.add(A) -> {G,A}

再找与<G,A>邻接且互相之间权最小并且未被访问的点，就找到了 B，

temp.add(B) -> {G,A,B}

以此类推，temp集合每次都增加一个顶点，相当于每次要比较与temp集合邻接且互相之间权最小并且未被访问的点。

直到所有顶点都被访问，也就是temp长度等于顶点数，结束。

数据结构（Java）最小生成树（普里姆、克鲁斯卡尔算法）

我把这个算法比喻成一个魔法宝石不断吸取周围能量，它最初很小，只有一个顶点。柿子专挑软的捏，它每次都从周围吸取一条与之邻接且权最小的边，转化为顶点不断壮大自己，然后再接着从外界吸收，直到它身边没有可以吸收的顶点了。

三、克鲁斯卡尔算法Kruskal

1) 克鲁斯卡尔 (Kruskal) 算法，是用来求加权连通图的最小生成树的算法。

2) 基本思想 ：按照权值从小到大的顺序选择 n-1 条边，并保证这 n-1 条边不构成回路

3) 具体做法 ：首先构造一个只含 n 个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止

可以看到这个算法的关键是 对边进行排序 、 把最小的边加入生成树 、 判断是否产生回路 。

前两个问题都好解决，关键是第三个问题如何解决呢？

我们要用一个数组来记录每个顶点的终点，就是能与之连通的最大顶点，这个数组会自动更新。感觉是这个算法的精髓。后面再写

同样的，我们用案例理解此算法：

数据结构（Java）最小生成树（普里姆、克鲁斯卡尔算法）

1)有北京有新增7个站点(A, B, C, D, E, F, G) ，现在需要修路把7个站点连通

2) 各个站点的距离用边线表示 ( 权 ) ，比如 A – B 距离 12 公里

3) 问：如何修路保证各个站点都能连通，并且总的修建公路总里程最短 ?

数据结构（Java）最小生成树（普里姆、克鲁斯卡尔算法）

四、代码演示

4.1 图的定义

class Graph {
    protected List<String> vertex;//存放顶点
    protected int[][] edges;//存放边
    protected boolean[] isVisited;//是否被访问
    protected int numOfEdges;

    public Graph(int n) {
        this.vertex = new ArrayList<>(n);
        this.edges = new int[n][n];
        this.isVisited = new boolean[n];
    }

    //常用方法
    // 1. 获取节点个数
    protected int getNumOfVertex() {
        return vertex.size();
    }

    // 2. 打印邻接矩阵
    protected void printGraph() {
        System.out.print(" ");
        for (String s : vertex) System.out.print("  " + s);
        System.out.println();
        for (int r = 0; r < vertex.size(); r++) {
            System.out.print(vertex.get(r) + " ");
            for (int c = 0; c < vertex.size(); c++) {
                System.out.print(String.format("%2d",edges[r][c]) + " ");
            }
            System.out.println();
        }
    }

    // 3. 获取边的数目
    protected int getNumOfEdges() {
        return numOfEdges;
    }

    // 4. 获取某条边的权值
    protected int getWeightOfEdges(int v1, int v2) {
        return edges[v1][v2];
    }

    // 5. 添加节点
    protected void addVertex(String v) {
        vertex.add(v);
    }

    // 6. 添加边（双向）
    protected void addEdge(int v1, int v2, int weight) {
        edges[v1][v2] = weight;
        edges[v2][v1] = weight;
        numOfEdges++;
    }

    // 7.获取顶点索引对应的值
    protected String getValueByIndex(int i) {
        return vertex.get(i);
    }
}

4.2 普里姆算法求最小生成树

  public static void prim(Graph graph, int v) {
        List<String> result = new ArrayList<>();//存放每次修的路径
        List<Integer> temp = new ArrayList<>();//存放每次遍历到的顶点索引
        temp.add(v);//先把初始点加进去
        graph.isVisited[v] = true;//标记为已访问
        int minRoute = Integer.MAX_VALUE;//暂存最短路径长度
        int nextVertex = 0;//暂存下一个顶点的索引(被连的顶点)
        int curVertex = 0;//暂存当前的顶点索引
        //temp满了说明所有点都连在一起了
        while (temp.size() < graph.getNumOfVertex()) {
            for (int j = 0; j < temp.size(); j++) {//每次从temp中取所有元素，集合在不断变大
                for (int i = 0; i < graph.getNumOfVertex(); i++) {//每次和所有顶点比较路径大小
                    if (graph.edges[temp.get(j)][i] != 0 && !graph.isVisited[i] && graph.edges[temp.get(j)][i] < minRoute) {
                        //对于路径不等零，而且没被访问的若干顶点，用中间变量记下最小的那个
                        minRoute = graph.edges[temp.get(j)][i];
                        nextVertex = i;
                        curVertex= temp.get(j) ;
                    }
                }
            }
            graph.isVisited[nextVertex] = true;//把最小的顶点标记已访问
            minRoute = Integer.MAX_VALUE;
            temp.add(nextVertex);//本次访问过的最小顶点加入集合中
            result.add(graph.getValueByIndex(curVertex) + " <-> " + graph.getValueByIndex(nextVertex));//记录每次哪两个顶点相连了
        }
        //输出最终结果
        System.out.println("各顶点间的连接线：");
        for (String e : result) System.out.println(e);
        System.out.println("顶点加入的先后次序：");
        for(Integer e:temp) System.out.print(graph.getValueByIndex(e)+" ");
    }

测试：

@Test
    public void testPrim() {
        Graph graph = new Graph(7);
        graph.addVertex("A");
        graph.addVertex("B");
        graph.addVertex("C");
        graph.addVertex("D");
        graph.addVertex("E");
        graph.addVertex("F");
        graph.addVertex("G");
        graph.addEdge(0, 1, 5);
        graph.addEdge(0, 2, 7);
        graph.addEdge(0, 6, 2);
        graph.addEdge(1, 6, 3);
        graph.addEdge(1, 3, 9);
        graph.addEdge(2, 4, 8);
        graph.addEdge(3, 5, 4);
        graph.addEdge(4, 5, 5);
        graph.addEdge(4, 6, 4);
        graph.addEdge(5, 6, 6);
        System.out.println("边的数量： " + graph.getNumOfEdges());
        System.out.println("顶点的数量： " + graph.getNumOfVertex());
        System.out.println("邻接矩阵：");
        graph.printGraph();
        minTree.prim(graph, 0);
    }



边的数量： 10
顶点的数量： 7
邻接矩阵：
   A  B  C  D  E  F  G
A  0  5  7  0  0  0  2 
B  5  0  0  9  0  0  3 
C  7  0  0  0  8  0  0 
D  0  9  0  0  0  4  0 
E  0  0  8  0  0  5  4 
F  0  0  0  4  5  0  6 
G  2  3  0  0  4  6  0 
各顶点间的连接线：
A <-> G
G <-> B
G <-> E
E <-> F
F <-> D
A <-> C
顶点加入的先后次序：
A G B E F D C

数据结构（Java）最小生成树（普里姆、克鲁斯卡尔算法）

4.3 克鲁斯卡尔算法求最小生成树

 public static void Kruskal(Graph graph) {
        int[] ends=new int[graph.getNumOfVertex()];//用于存放顶点的终点信息
        List<String> result = new ArrayList<>();//存放每次连接的路径
        //1、把顶点都存到一个新的数组中，然后权值从小到大排序。
        // 数组元素第一个是权，后两个是两个顶点。因为无向图对称，所以只要右上部分
        int[][] edgeData=new int[graph.getNumOfEdges()][3];
        for(int i=0,count=0;i< graph.getNumOfVertex() && count< graph.getNumOfEdges();i++){
            for(int j=i+1;j< graph.getNumOfVertex();j++){
                if(graph.edges[i][j]!=0) {
                    edgeData[count][0]=graph.edges[i][j];
                    edgeData[count][1]=i;
                    edgeData[count][2]=j;
                    count++;
                }
            }
        }
        Arrays.sort(edgeData, (e1,e2)->e1[0]-e2[0]);//先按第一列元素升序排序，如果第一列相等再按第二列元素升序；
        //2、依次取出edgeData中权值较小的边，判断其两个顶点的终点，如果构不成回路就加入，否则不加
        for(int i=0;i< edgeData.length;i++){
            int v1=getEnd(ends,edgeData[i][1]);
            int v2=getEnd(ends,edgeData[i][2]);
            if(v1!=v2){
                ends[v1]=v2;//v1的终点设为v2
                //记录哪两个顶点相连
                result.add("<"+ graph.getValueByIndex(edgeData[i][1])+","+graph.getValueByIndex(edgeData[i][2])+">");
            }
        }
        //3、输出最终结果
        System.out.println("各顶点间的连接线：");
        for (String e : result) System.out.println(e);
    }
    //获取某个顶点的终点，更新ends数组。这是精髓
    private static int getEnd(int[] ends,int index) {
        //如果当前顶点有终点，那就让它循环指向终点，相当于有一个指针;没有的话返回它自己
        while (ends[index]!=0) index=ends[index];
        return index;
    }
    }

测试：

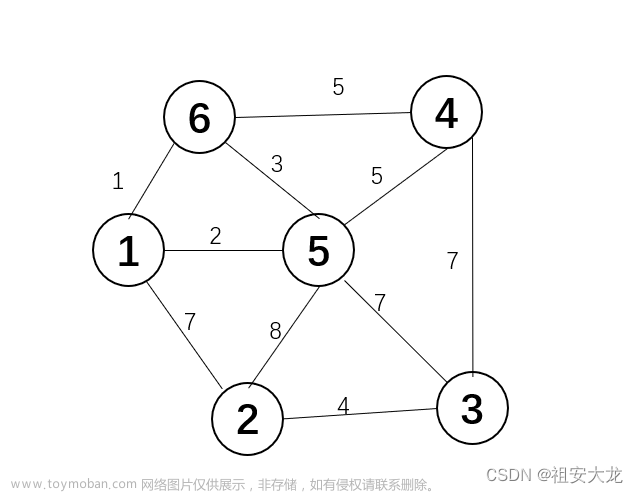
 @Test
    public void testKruskal() {
        Graph graph = new Graph(7);
        graph.addVertex("A");
        graph.addVertex("B");
        graph.addVertex("C");
        graph.addVertex("D");
        graph.addVertex("E");
        graph.addVertex("F");
        graph.addVertex("G");
        graph.addEdge(0, 1, 12);
        graph.addEdge(0, 5, 16);
        graph.addEdge(0, 6, 14);
        graph.addEdge(1, 2, 10);
        graph.addEdge(1, 5, 7);
        graph.addEdge(2, 3, 3);
        graph.addEdge(2, 4, 5);
        graph.addEdge(2, 5, 6);
        graph.addEdge(3, 4, 4);
        graph.addEdge(4, 5, 2);
        graph.addEdge(4, 6, 8);
        graph.addEdge(5, 6, 9);
        System.out.println("边的数量： " + graph.getNumOfEdges());
        System.out.println("顶点的数量： " + graph.getNumOfVertex());
        System.out.println("邻接矩阵：");
        graph.printGraph();
        minTree.Kruskal(graph);
    }



边的数量： 12
顶点的数量： 7
邻接矩阵：
   A  B  C  D  E  F  G
A  0 12  0  0  0 16 14 
B 12  0 10  0  0  7  0 
C  0 10  0  3  5  6  0 
D  0  0  3  0  4  0  0 
E  0  0  5  4  0  2  8 
F 16  7  6  0  2  0  9 
G 14  0  0  0  8  9  0 
各顶点间的连接线：
<E,F>
<C,D>
<D,E>
<B,F>
<E,G>
<A,B>

数据结构（Java）最小生成树（普里姆、克鲁斯卡尔算法）