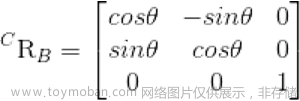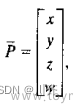一、解的存在性与多重性
逆运动学是一个非线性的求解问题,相对于正运动学较为复杂,主要是因为可解性探究、多重解以及多重解的选择等问题。例如,形如【机器人学】正运动学详解-6.4 一个简单例子中所用的六自由度机器人,其逆运动学可以描述为:假设我们已经知道其次变换矩阵 R T H ^RT_H RTH中的16个元素,求解得到6个关节变量 θ 1 \theta_1 θ1~ θ 6 \theta_6 θ6。由于矩阵 R T H ^RT_H RTH中有4个元素为常量,因此我们可以根据矩阵相等的条件得到12个等式,但是我们要注意到这12个方程之间有着相互约束,根据旋转矩阵得到的9个元素中,实际只有3个相互独立,再结合位置矢量的3个方程,那么我们将足够得到非齐次方程的解,这就是逆运动学。
- 解的存在性
解的存在性取决于该机器人的工作空间,通俗地说,就是机器人基座固定的情况下末端执行器所能够运动到的空间范围。但是我们应该看到,对于逆运动学,不仅要求位置矢量在工作空间内,姿态也达到要求才能算作逆运动学的解。机器人的工作空间主要分成3类,包括可达工作空间、灵活工作空间和次工作空间。可达工作空间是指机器人正常运行时,末端执行器坐标系的原点能在空间活动的最大范围;灵活工作空间是指在总工作空间内,末端执行器可以任意姿态达到的点;次工作空间是指总工作空间中去除灵活工作空间后所余下的部分构成的工作空间。
当一个机器人少于6自由度时,它在三维空间内不能达到全部位姿,特别是在工作空间的边界,一般来说能达到的位姿较少。
- 多重解问题
如果逆运动学只对位置有要求或者欧拉角只有部分要求时,容易出现有多个解的情况。这时,我们首先需要将所有这些解都得到,另外,我们还需要根据一定的原则来选择其中的解,常用的选择原则有“最短路程”、“最小能量”等,“最短行程”下的解即为在关节的运动范围内选择一组使得各个关节角的变化量最小的解。根据“最短行程”的原则来选择运动学逆解时也存在多种选择方式,例如对各关节的变化量进行不同的加权,使得选择的解尽量移动靠近末端执行器的连杆。“最小能量”即选择一组使得关节角变化所需能量最小的解。
二、逆运动学的几何解法
本文将提供一个经典的几何解法案例:
一个三杆平面机械臂中,末端执行器的位姿为
X
3
X_3
X3与
X
0
X_0
X0之间的夹角
ϕ
\phi
ϕ,位置矢量为
[
x
y
0
]
T
\left[\begin{matrix}x&y&0\end{matrix}\right]^T
[xy0]T,杆件1和2的长度分别为
L
1
L_1
L1和
L
2
L_2
L2,求解
θ
1
\theta_1
θ1~
θ
3
\theta_3
θ3.
根据三角形几何关系和余弦定理,我们可以得到:
x
2
+
y
2
=
L
1
2
+
L
2
2
−
2
L
1
L
2
cos
(
180
+
θ
2
)
=
L
1
2
+
L
2
2
+
2
L
1
L
2
cos
(
θ
2
)
(1)
\begin{aligned} x^2+y^2&=L_1^2+L_2^2-2L_1L_2\cos(180+\theta_2)\\ &=L_1^2+L_2^2+2L_1L_2\cos(\theta_2) \end{aligned}\tag{1}
x2+y2=L12+L22−2L1L2cos(180+θ2)=L12+L22+2L1L2cos(θ2)(1)
因此,
cos
θ
2
=
x
2
+
y
2
−
L
1
2
−
L
2
2
2
L
1
L
2
(2)
\cos\theta_2=\frac{x^2+y^2-L_1^2-L_2^2}{2L_1L_2}\tag{2}
cosθ2=2L1L2x2+y2−L12−L22(2)
如果
∣
x
2
+
y
2
−
L
1
2
−
L
2
2
2
L
1
L
2
∣
>
1
|\frac{x^2+y^2-L_1^2-L_2^2}{2L_1L_2}|>1
∣2L1L2x2+y2−L12−L22∣>1,无解;
如果 x 2 + y 2 − L 1 2 − L 2 2 2 L 1 L 2 = ± 1 \frac{x^2+y^2-L_1^2-L_2^2}{2L_1L_2}=\pm1 2L1L2x2+y2−L12−L22=±1,那么 θ 2 = π 2 ∓ π 2 \theta_2=\frac{\pi}{2}\mp\frac{\pi}{2} θ2=2π∓2π;
如果 ∣ x 2 + y 2 − L 1 2 − L 2 2 2 L 1 L 2 ∣ < 1 |\frac{x^2+y^2-L_1^2-L_2^2}{2L_1L_2}|<1 ∣2L1L2x2+y2−L12−L22∣<1,那么 θ 2 = ± arccos [ x 2 + y 2 − L 1 2 − L 2 2 2 L 1 L 2 ] \theta_2=\pm \arccos\left[\frac{x^2+y^2-L_1^2-L_2^2}{2L_1L_2}\right] θ2=±arccos[2L1L2x2+y2−L12−L22]。
根据几何关系易得:
β = arctan y x \beta=\arctan\frac{y}{x} β=arctanxy
cos ψ = x 2 + y 2 + L 1 2 − L 2 2 2 L 1 x 2 + y 2 \cos\psi=\frac{x^2+y^2+L_1^2-L_2^2}{2L_1\sqrt{x^2+y^2}} cosψ=2L1x2+y2x2+y2+L12−L22,那么可得: ψ = arccos x 2 + y 2 + L 1 2 − L 2 2 2 L 1 x 2 + y 2 \psi=\arccos\frac{x^2+y^2+L_1^2-L_2^2}{2L_1\sqrt{x^2+y^2}} ψ=arccos2L1x2+y2x2+y2+L12−L22。
如果 θ 2 ≤ 0 \theta_2\le0 θ2≤0,那么 θ 1 = β + ψ \theta_1=\beta+\psi θ1=β+ψ;
如果 θ 2 > 0 \theta_2>0 θ2>0,那么 θ 1 = β − ψ \theta_1=\beta-\psi θ1=β−ψ;
最后, θ 3 = ϕ − θ 1 − θ 2 \theta_3=\phi-\theta_1-\theta_2 θ3=ϕ−θ1−θ2。
三、逆运动学的代数解法
为了简化模型与学习方便,本方法将以【机器人学】正运动学详解-6.4 一个简单例子的前4个自由度形成的机械臂作为例子,结合之前所学正运动学中的修改DH法,对逆运动学的代数解法进行一个方法示例。
只看前四个节点,那么对其建系建模如下:
DH表:
| # | θ \theta θ | d d d | a a a | α \alpha α |
|---|---|---|---|---|
| 0—1 | θ 1 \theta_1 θ1 | 0 | 0 | 0° |
| 1—2 | θ 2 \theta_2 θ2 | 0 | 0 | 90° |
| 2—3 | θ 3 \theta_3 θ3 | 0 | a 2 a_2 a2 | 0° |
| 3—4 | θ 4 \theta_4 θ4 | 0 | a 3 a_3 a3 | 0° |
因此我们可以得到相邻坐标系的齐次变换矩阵:
0
T
1
=
[
c
θ
1
−
s
θ
1
0
0
s
θ
1
c
θ
1
0
0
0
0
1
0
0
0
0
1
]
,
1
T
2
=
[
c
θ
2
−
s
θ
2
0
0
0
0
−
1
0
s
θ
2
c
θ
2
0
0
0
0
0
1
]
2
T
3
=
[
c
θ
3
−
s
θ
3
0
a
2
s
θ
3
c
θ
3
0
0
0
0
1
0
0
0
0
1
]
,
3
T
4
=
[
c
θ
4
−
s
θ
4
0
a
3
s
θ
4
c
θ
4
0
0
0
0
1
0
0
0
0
1
]
(3)
\begin{aligned} &^0T_1=\left[\begin{matrix}c\theta_1&-s\theta_1&0&0\\ s\theta_1&c\theta_1&0&0\\ 0&0&1&0\\ 0&0&0&1\end{matrix}\right],^1T_2=\left[\begin{matrix}c\theta_2&-s\theta_2&0&0\\0&0&-1&0\\ s\theta_2&c\theta_2&0&0\\0&0&0&1\end{matrix}\right]\\ &^2T_3=\left[\begin{matrix}c\theta_3&-s\theta_3&0&a_2\\ s\theta_3&c\theta_3&0&0\\ 0&0&1&0\\0&0&0&1\end{matrix}\right],^3T_4=\left[\begin{matrix}c\theta_4&-s\theta_4&0&a_3\\ s\theta_4&c\theta_4&0&0\\ 0&0&1&0\\0&0&0&1\end{matrix}\right] \end{aligned}\tag{3}
0T1=⎣
⎡cθ1sθ100−sθ1cθ10000100001⎦
⎤,1T2=⎣
⎡cθ20sθ20−sθ20cθ200−1000001⎦
⎤2T3=⎣
⎡cθ3sθ300−sθ3cθ3000010a2001⎦
⎤,3T4=⎣
⎡cθ4sθ400−sθ4cθ4000010a3001⎦
⎤(3)
因此,该机器人的手(末端执行器)所在坐标系
{
H
}
\{H\}
{H}相对于机器人基座
{
R
}
\{R\}
{R}的齐次变换矩阵
R
T
H
^RT_H
RTH为:
R
T
H
=
0
T
1
×
1
T
2
×
2
T
3
×
3
T
4
=
[
c
1
c
234
−
c
1
s
234
s
1
c
1
(
a
2
c
2
+
a
3
c
23
)
s
1
c
234
−
s
1
s
234
−
c
1
s
1
(
a
2
c
2
+
a
3
c
23
)
s
234
c
234
0
a
2
s
2
+
a
3
s
23
0
0
0
1
]
=
[
n
x
o
x
a
x
p
x
n
y
o
y
a
y
p
y
n
z
o
z
a
z
p
z
0
0
0
1
]
(4)
\begin{aligned} ^RT_H&=^0T_1\times^1T_2\times^2T_3\times^3T_4\\ &=\left[\begin{matrix} c_1c_{234}&-c_1s_{234}&s_1&c_1(a_2c_2+a_3c_{23})\\ s_1c_{234}&-s_1s_{234}&-c_1&s_1(a_2c_2+a_3c_{23})\\ s_{234}&c_{234}&0&a_2s_2+a_3s_{23}\\ 0&0&0&1 \end{matrix}\right]\\ &=\left[\begin{matrix} n_x&o_x&a_x&p_x\\ n_y&o_y&a_y&p_y\\ n_z&o_z&a_z&p_z\\ 0&0&0&1 \end{matrix}\right] \end{aligned}\tag{4}
RTH=0T1×1T2×2T3×3T4=⎣
⎡c1c234s1c234s2340−c1s234−s1s234c2340s1−c100c1(a2c2+a3c23)s1(a2c2+a3c23)a2s2+a3s231⎦
⎤=⎣
⎡nxnynz0oxoyoz0axayaz0pxpypz1⎦
⎤(4)
列出方程组:
{
n
x
=
c
1
c
234
(
a
)
n
y
=
s
1
c
234
(
b
)
n
z
=
s
234
(
c
)
o
x
=
−
c
1
s
234
(
d
)
o
y
=
−
s
1
s
234
(
e
)
o
z
=
c
234
(
f
)
a
x
=
s
1
(
g
)
a
y
=
−
c
1
(
h
)
a
z
=
0
(
i
)
p
x
=
c
1
(
a
2
c
2
+
a
3
c
23
)
(
j
)
p
y
=
s
1
(
a
2
c
2
+
a
3
c
23
)
(
k
)
p
z
=
a
2
s
2
+
a
3
s
23
(
l
)
(5)
\begin{equation} \left\{ \begin{array}{lr} n_x=c_1c_{234}&(a)\\ n_y=s_1c_{234}&(b)\\ n_z=s_{234}&(c)\\ o_x=-c_1s_{234}&(d)\\ o_y=-s_1s_{234}&(e)\\ o_z=c_{234}&(f)\\ a_x=s_1&(g)\\ a_y=-c_1&(h)\\ a_z=0&(i)\\ p_x=c_1(a_2c_2+a_3c_{23})&(j)\\ p_y=s_1(a_2c_2+a_3c_{23})&(k)\\ p_z=a_2s_2+a_3s_{23}&(l)\\ \end{array} \right. \end{equation}\tag{5}
⎩
⎨
⎧nx=c1c234ny=s1c234nz=s234ox=−c1s234oy=−s1s234oz=c234ax=s1ay=−c1az=0px=c1(a2c2+a3c23)py=s1(a2c2+a3c23)pz=a2s2+a3s23(a)(b)(c)(d)(e)(f)(g)(h)(i)(j)(k)(l)(5)
因此,我们可以得到:
θ
1
=
{
±
π
2
a
y
=
0
,
a
x
=
±
1
a
t
a
n
2
(
a
x
,
−
a
y
)
a
y
≠
0
(6)
\theta_1= \left\{\begin{array}{lr} \pm\frac{\pi}{2}&a_y=0,a_x=\pm1\\ atan2(a_x,-a_y)&a_y\neq0 \end{array} \right. \tag{6}
θ1={±2πatan2(ax,−ay)ay=0,ax=±1ay=0(6)
θ 234 = θ 2 + θ 3 + θ 4 = { ± π 2 o z = 0 , n z = ± 1 a t a n 2 ( n z , o z ) o z ≠ 0 (7) \theta_{234}=\theta_2+\theta_3+\theta_4= \left\{\begin{array}{lr} \pm\frac{\pi}{2}&o_z=0,n_z=\pm1\\ atan2(n_z,o_z)&o_z\neq0 \end{array} \right. \tag{7} θ234=θ2+θ3+θ4={±2πatan2(nz,oz)oz=0,nz=±1oz=0(7)
令
m
=
a
2
c
2
+
a
3
c
23
=
{
p
x
−
a
y
a
y
≠
0
p
y
a
x
a
y
=
0
m=a_2c_2+a_3c_{23}=\left\{\begin{array}{lr}\frac{p_x}{-a_y}&a_y\neq0\\\frac{p_y}{a_x}&a_y=0\end{array} \right.
m=a2c2+a3c23={−aypxaxpyay=0ay=0,
n
=
a
2
s
2
+
a
3
s
23
=
p
z
n=a_2s_2+a_3s_{23}=p_z
n=a2s2+a3s23=pz,那么:
m
2
+
n
2
=
a
2
2
+
a
3
2
+
2
a
2
a
3
c
2
c
23
+
2
a
2
a
3
s
2
s
23
=
a
2
2
+
a
3
2
+
2
a
2
a
3
c
3
(8)
m^2+n^2=a_2^2+a_3^2+2a_2a_3c_2c_{23}+2a_2a_3s_2s_{23}=a_2^2+a_3^2+2a_2a_3c_3\tag{8}
m2+n2=a22+a32+2a2a3c2c23+2a2a3s2s23=a22+a32+2a2a3c3(8)
θ 3 = ± arccos ( m 2 + n 2 − a 2 2 − a 3 2 2 a 2 a 3 ) (9) \theta_3=\pm\arccos\left(\frac{m^2+n^2-a_2^2-a_3^2}{2a_2a_3}\right)\tag{9} θ3=±arccos(2a2a3m2+n2−a22−a32)(9)
根据
m
m
m和
n
n
n可得:
{
c
23
=
m
−
a
2
c
2
a
3
s
23
=
n
−
a
2
s
2
a
3
(10)
\begin{equation} \left\{\begin{array}{lr} c_{23}=\frac{m-a_2c_2}{a_3}\\\\ s_{23}=\frac{n-a_2s_2}{a_3} \end{array} \right. \end{equation}\tag{10}
⎩
⎨
⎧c23=a3m−a2c2s23=a3n−a2s2(10)
根据正余弦函数的规律,可知:
(
m
−
a
2
c
2
)
2
+
(
n
−
a
2
s
2
)
2
=
m
2
+
n
2
+
a
2
2
−
2
a
2
(
m
c
2
+
n
s
2
)
=
a
3
2
(11)
(m-a_2c_2)^2+(n-a_2s_2)^2=m^2+n^2+a_2^2-2a_2(mc_2+ns_2)=a_3^2\tag{11}
(m−a2c2)2+(n−a2s2)2=m2+n2+a22−2a2(mc2+ns2)=a32(11)
假设
α
=
a
t
a
n
2
(
m
,
n
)
\alpha=atan2(m,n)
α=atan2(m,n),那么:
m
2
+
n
2
sin
(
θ
2
+
α
)
=
m
2
+
n
2
+
a
2
2
−
a
3
2
2
a
2
(12)
\sqrt{m^2+n^2}\sin(\theta_2+\alpha)=\frac{m^2+n^2+a_2^2-a_3^2}{2a_2}\tag{12}
m2+n2sin(θ2+α)=2a2m2+n2+a22−a32(12)
θ 2 = π 2 ± ( π 2 − arcsin m 2 + n 2 + a 2 2 − a 3 2 2 a 2 m 2 + n 2 ) − α (13) \theta_2=\frac{\pi}{2}\pm\left(\frac{\pi}{2}-\arcsin\frac{m^2+n^2+a_2^2-a_3^2}{2a_2\sqrt{m^2+n^2}}\right)-\alpha\tag{13} θ2=2π±(2π−arcsin2a2m2+n2m2+n2+a22−a32)−α(13)文章来源:https://www.toymoban.com/news/detail-401488.html
最终,
θ
4
\theta_4
θ4可以根据上述表达式得到:
θ
4
=
θ
234
−
θ
2
−
θ
3
(14)
\theta_4=\theta_{234}-\theta_2-\theta_3\tag{14}
θ4=θ234−θ2−θ3(14)文章来源地址https://www.toymoban.com/news/detail-401488.html
到了这里,关于【机器人学】逆运动学的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!