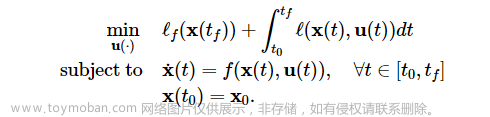本文编辑:调皮哥的小助理
众所周知,通常雷达在检测目标时如果目标是靠近雷达做径向运动,目标速度的速度就是正的。反之,如果目标是远离雷达做径向运动的,那么目标的速度就是负的。
但是线性调频连续波(FMCW)雷达却不是这样的,刚好和上述结论相反。即目标靠近雷达做径向运动,则目标速度为负;目标远离雷达做径向运动,目标速度为正。
这个结论是如何来的,为何调频连续波雷达和一般的脉冲雷达不一样呢?下面针对这个问题,我们一起来研究一下。首先为了弄清楚脉冲雷达和调频连续波雷达测速原理的区别,先对脉冲雷达的测速原理进行梳理。
1.脉冲雷达测速原理
脉冲雷达测速靠的是多普勒频移,公式推导过程如下:
(1)多普勒频率公式推导方法一
假设,雷达与目标之间的距离为R,则在雷达到达目标并且返回的双程路径2R中,波长λ的总数为2R/λ,每个波长对应2π(rad)的相位变化,因此双路程2R的总相位变化就是:
ϕ = 2 π ⋅ 2 R λ = 4 π R λ \phi=2 \pi \cdot \frac{2 R}{\lambda}=\frac{4 \pi R}{\lambda} ϕ=2π⋅λ2R=λ4πR
如果目标相对雷达做径向运动,那么R和相位的值就会随着时间的变化而变化。求出相位与时间的导数,便可得到相位随时间的变化率,即角频率。
ω = Δ ϕ Δ t = 4 π λ ⋅ Δ R Δ t = 4 π v λ = 2 π f d \omega=\frac{\Delta \phi}{\Delta t}=\frac{4 \pi}{\lambda} \cdot \frac{\Delta R}{\Delta t}=\frac{4 \pi v}{\lambda}=2 \pi f_d ω=ΔtΔϕ=λ4π⋅ΔtΔR=λ4πv=2πfd
其中,距离变化率对时间的导数就是目标的径向速度,相位随着时间的变化率就是角频率w=2πfd,这里的fd就是多普勒频移。
故而最终得到目标径向运动的速度和多普勒频率之间的关系如下:
f d = 2 v λ f_d=\frac{2 v}{\lambda} fd=λ2v
其中,fd为目标的多普勒频率,v为目标径向运动的速度,λ为发射信号波长。由上述公式可以得到,目标径向运动的速度由目标的多普勒频率决定。即:
v = λ f d 2 v=\frac{\lambda f_d}{2} v=2λfd
(2)脉冲雷达目标径向运动速度与多普勒频率的正负关系
由上述推导的公式可知,当目标靠近雷达时,多普勒频率为正,则目标速度为正;当目标远离雷达时,多普勒频率为负,则目标速度为负。
那么为什么是这样呢?下面来证明这个结论是否正确。上述推导的多普勒频率与目标径向运动速度的关系的公式,是一种比较简单的方法,但是这种方法用于推导脉冲雷达目标径向运动速度与多普勒频率的正负关系还不是很严谨。
下面用另一种方式来推导多普勒频率公式的方法来证明该结论。首先,假设发射信号频率为ft,则发射信号模型可以表示为:
s t ( t ) = A t sin ( 2 π f t t ) s_t(t)=A_t \sin \left(2 \pi f_t t\right) st(t)=Atsin(2πftt)
则接收信号可以表示为:
s r ( t ) = A r sin [ 2 π f t ( t − T R ) ] s_r(t)=A_r \sin \left[2 \pi f_t\left(t-T_R\right)\right] sr(t)=Arsin[2πft(t−TR)]
其中At和Ar分别表示接收和发射信号的幅度。往返的时TR=2R/c。如果目标靠近雷达运动,则距离就会发生变化R=R0-vt,其中v是目标的径向速度。故而可以将接收信号表示为:
s r ( t ) = A r sin [ 2 π f t ( t − T R ) ] = A r sin { 2 π f t ( t − 2 ( R 0 − v t ) c ) } = A r sin { 2 π f t ( 2 v c + 1 ) t − 4 π R 0 f t c } \begin{aligned} s_r(t) &=A_r \sin \left[2 \pi f_t\left(t-T_R\right)\right] \\ &=A_r \sin \left\{2 \pi f_t\left(t-\frac{2\left(R_0-v t\right)}{c}\right)\right\} \\ &=A_r \sin \left\{2 \pi f_t\left(\frac{2 v}{c}+1\right) t-\frac{4 \pi R_0 f_t}{c}\right\} \end{aligned} sr(t)=Arsin[2πft(t−TR)]=Arsin{2πft(t−c2(R0−vt))}=Arsin{2πft(c2v+1)t−c4πR0ft}
其中可以推导出,目标的多普勒频移为:
2
π
f
t
(
2
v
c
+
1
)
t
=
2
π
f
0
t
2 \pi f_t\left(\frac{2 v}{c}+1\right) t=2 \pi f_0 t
2πft(c2v+1)t=2πf0t
f
0
=
f
t
(
2
v
c
+
1
)
=
2
v
f
t
c
+
f
t
=
2
v
λ
+
f
t
=
f
d
+
f
t
f_0=f_t\left(\frac{2 v}{c}+1\right)=\frac{2 v f_t}{c}+f_t=\frac{2 v}{\lambda}+f_t=f_d+f_t
f0=ft(c2v+1)=c2vft+ft=λ2v+ft=fd+ft
f
d
=
f
0
−
f
t
=
2
v
λ
f_d=f_0-f_t=\frac{2 v}{\lambda}
fd=f0−ft=λ2v
上述等式为多普勒频移的定义式,即为多普勒频率一般定义为接收频率和发射频率的差值。故而目标靠近雷达做径向运动速度与多普勒频率的正负关系如下:
v = λ f d 2 v=\frac{\lambda f_d}{2} v=2λfd
假设目标向后运动,则距离就会发生变化R=R0+vt,其中v是目标的径向速度。故而又可以将接收信号表示为:
s r ( t ) = A r sin [ 2 π f t ( t − T R ) ] = A r sin { 2 π f t ( t − 2 ( R 0 + v t ) c ) } = A r sin { 2 π f t ( 1 − 2 v c ) t − 4 π R 0 f t c } \begin{aligned} s_r(t) &=A_r \sin \left[2 \pi f_t\left(t-T_R\right)\right] \\ &=A_r \sin \left\{2 \pi f_t\left(t-\frac{2\left(R_0+v t\right)}{c}\right)\right\} \\ &=A_r \sin \left\{2 \pi f_t\left(1-\frac{2 v}{c}\right) t-\frac{4 \pi R_0 f_t}{c}\right\} \end{aligned} sr(t)=Arsin[2πft(t−TR)]=Arsin{2πft(t−c2(R0+vt))}=Arsin{2πft(1−c2v)t−c4πR0ft}
其中可以推导出,目标的多普勒频移为:
2
π
f
t
(
1
−
2
v
c
)
t
=
2
π
f
0
t
2 \pi f_t\left(1-\frac{2 v}{c}\right) t=2 \pi f_0 t
2πft(1−c2v)t=2πf0t
f
0
=
f
t
(
1
−
2
v
c
)
=
f
t
−
2
v
c
f
t
=
f
t
−
2
v
λ
=
f
t
−
f
d
f_0=f_t\left(1-\frac{2 v}{c}\right)=f_t-\frac{2 v}{c} f_t=f_t-\frac{2 v}{\lambda}=f_t-f_d
f0=ft(1−c2v)=ft−c2vft=ft−λ2v=ft−fd
f
d
=
f
0
−
f
t
=
−
2
v
λ
f_d=f_0-f_t=-\frac{2 v}{\lambda}
fd=f0−ft=−λ2v
上述等式即可推导出,多普勒频率为负,则故而目标远离雷达做径向运动速度与多普勒频率的正负关系如下::
v = − λ f d 2 v=-\frac{\lambda f_d}{2} v=−2λfd
由此可知脉冲雷达的速度与多普勒频率的关系是:当目标靠近雷达时,多普勒频率为正,目标速度为正;当目标远离雷达时,多普勒频率为负,目标速度为负。
2.调频连续波雷达测速原理
调频连续波雷达刚好相反,即当目标靠近雷达时,目标速度为负;当目标远离雷达时,目标速度为正。
脉冲雷达测速利用的是多普勒频移,调频连续波用的是脉冲之间的初相位差。对于两个相邻周期的信号,由于周期间隔时间Tc较短,距离分辨率有限,两个周期的距离维FFT谱中的峰值位置基本没有发生变化(近似值)。中频信号的初相近似为:
ϕ 0 = 4 π R λ \phi_0=\frac{4 \pi R}{\lambda} ϕ0=λ4πR
即周期间的微小距离变化会引起中频信号初相的变化,由傅里叶变换特性可知,信号的初相体现在 峰值处的复数值对应的相位。计算相邻周期的初相位差,可以获得目标的速度。
Δ ϕ = 4 π v T c λ v = λ Δ ϕ 4 π T c \begin{aligned} \Delta \phi &=\frac{4 \pi v T_c}{\lambda} \\ v &=\frac{\lambda \Delta \phi}{4 \pi T_c} \end{aligned} Δϕv=λ4πvTc=4πTcλΔϕ
故而,调频连续波的速度与脉冲之间的初相位差有关,其正负由初相位差的正负来决定。当目标靠近雷达时,目标与雷达之间的距离R逐渐减小,当前脉冲信号的初相与上一周期脉冲的初相差值,等效于当前距离与上一个周期的距离的差值,因此随着雷达的靠近,距离差值为负,相位差也为负,故而速度为负。
同理,当目标远离雷达时,目标与雷达之间的距离R逐渐增大,当前脉冲信号的初相与上一周期脉冲的初相差值,等效于当前距离与上一个周期的距离的差值,因此随着雷达的远离,距离差值为正,相位差也为正,故而速度为正。
3.示例
通常我们用MATLAB做信号处理时,需要对目标的速度进行分析,而目标的运动方向与速度的关系,是做调频连续波雷达必须搞清楚的关键点。
如图3-1是实际采集的数据做分析得到的图,是两个目标面向运动。两个目标分别由近及远、由远及近移动,速度一快一慢,移动较为平稳时开始采集信号。
可以看到两个目标的距离分别为 2.038m和 4.407m,速度分别为 1.202m/s 和-1.603m/s。两个目标峰值大小不同,是因为数据采集时刻两者与雷达的距离不同,距离雷达较近的目标反射回波能量较大,信噪比高,处理结果峰值越高,反之,距离雷达较远的目标反射回波的能量较小,信噪比低,峰值较低。上述这个过程就是速度维FFT。
(图3-1 双目标面向运动效果)文章来源:https://www.toymoban.com/news/detail-401596.html
感谢阅读,希望对你有帮助,记得给调皮哥点赞!文章来源地址https://www.toymoban.com/news/detail-401596.html
到了这里,关于雷达原理 | 讨论调频连续波雷达目标运动方向与速度正负的关系?的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!