0. 关于本项目
首先附上本项目的GitHub仓库
本项目使用STM32F103C8T6作为主控,Keil5开发,Mahony算法进行姿态解算的平衡车。项目中给出了MPU6050、ICM20602、ICM42605三种主流IMU的驱动。目前仅实现了直立平衡,在设计设加入了BlueTooth模块,手机遥控部分还在开发中(新建文件夹) (°ー°〃)
首先需要的前提知识有:
- Keil5的使用
- STM32有一定了解
- 电机驱动的原理,使用
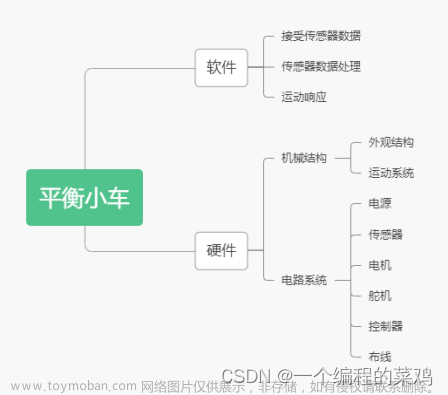
1. 硬件
1.1 器件购买
要制作一台平衡小车,需要用到的硬件材料有:轮子、带编码器的直流电机、电机排线、面包板、杜邦线、STM32、稳压模块、蓝牙模块、电机驱动模块、陀螺仪模块、超声波模块、电池、底盘、螺栓、铜柱、固定轧带、开关等。下面是物料表:
| 类型 | 链接 | 数量 |
|---|---|---|
MG513P20_12V 电机 |
直流减速电机带光电霍尔编码器码盘测速 | 1 |
| 电池 | 2S锂电池及充电器 | 1 |
5V DCDC稳压 |
DCDC降压模块 12V转5V3A | 1 |
LCD ST7789主控 240×240 |
1.3寸ips TFT显示屏ips液晶屏 | 1 |
其余器件见下表格
| ID | 名称 | 型号 | 数量 |
|---|---|---|---|
| 1 | STM32最小系统板 | STM32F103C8T6 | 1 |
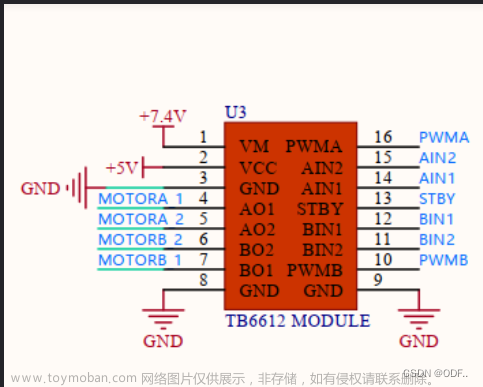
| 2 | 电机驱动 | TB6612FNG | 1 |
| 3 | 陀螺仪 | MPU6050或ICM42605、20602 | 1 |
| 4 | 蓝牙 | HC-07 | 1 |
| 5 | 10uF钽电容 | 6.3V,3528,3.52.82.1mm | 1 |
| 6 | 20uF钽电容 | 6.3V,3528,3.52.82.1mm | 1 |
| 7 | 电机插座、排线 | 6P-2.54mm 10cm排线 | 2 |
| 8 | T型头 | 航模电池T型头 | 1 |
| 9 | AMS1117-3.3V | AMS1117-3.3V贴片 | 1 |
| 10 | 开关 | 摇臂开关 | 2 |
| 11 | 铜柱 | 六角3mm | 若干 |
| 12 | 扎带 | 3.6mm | 若干 |
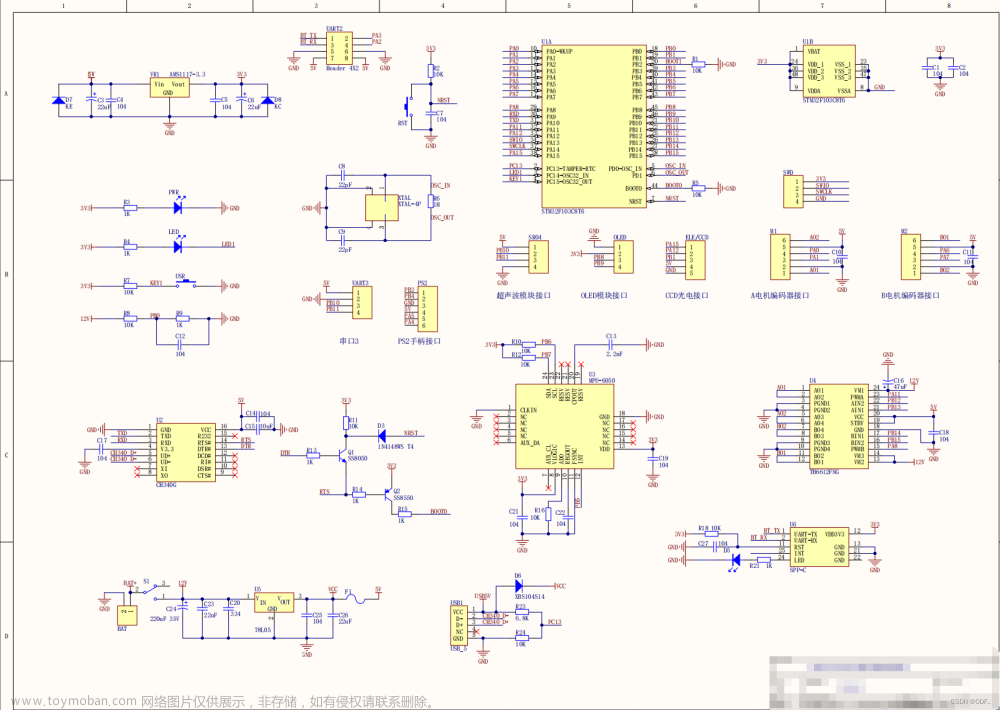
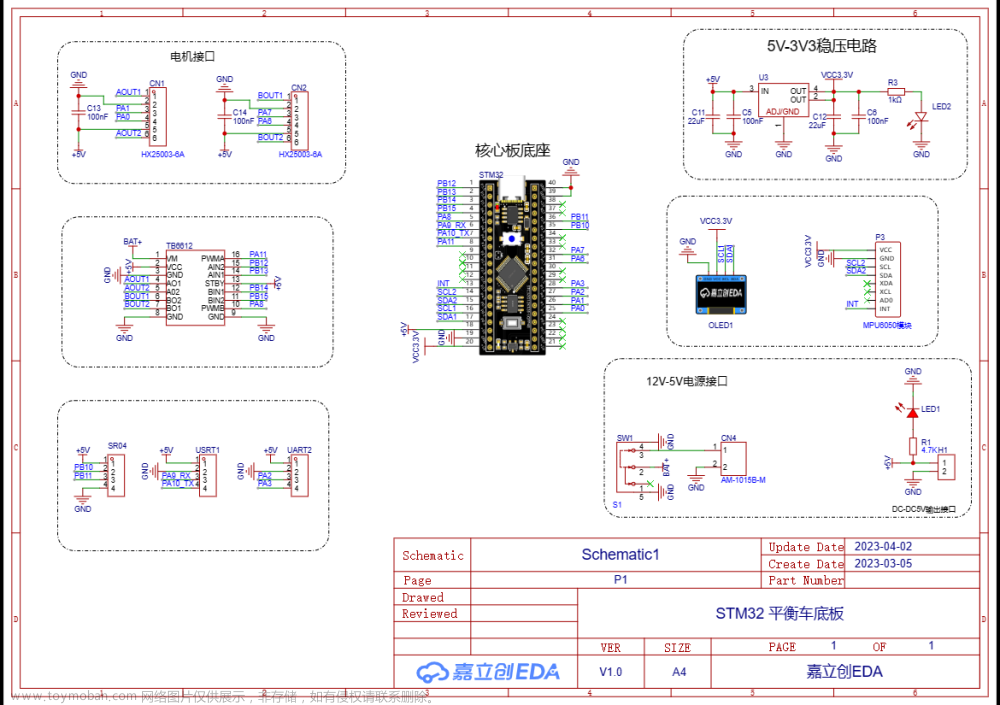
1.2 PCB
目前是第一版,画的很菜,用到的都是插接件,线也布的很乱 (:3」∠)。后续还会更新PCB(计划换成贴片,体积会更小)

1.3 车模

SolidWorks画的简单底板尺寸如图(mm),用3D打印机制造,源文件在学校电脑上,回学校了再上传。
2. 算法
2.1 PID算法
2.1.1 理论分析
该项目为使的小车平衡最主要的两个环就是直立环和速度环,通过叠加得到最终给电机的输出,这也是网上绝大多数的小车平衡控制方法。
- 我们先使用常规的速度负反馈算法想象一下。首先我们给定一个目标速度值,由于小车在直立控制的作用下,此时小车要向前倾斜以获取加速度,车轮需要往后运动,这样小车速度就会下降。因为是负反馈,速度下降之后,速度控制的偏差增大,小车往前倾斜的角度增大,如此反复,小车便会倒下。
- 为保证直立控制的优先级,我们把速度控制放在直立控制的前面,也就是速度控制调节的结果仅仅是改变直立控制的目标值。因为根据经验可知,小车的运行速度和小车的倾角是相关的。比如要提高小车向前行驶的速度,就需要增加小车向前倾斜的角度,倾斜角度加大之后,车轮在直立控制的作用下需要向前运动。因此直立环的
Kp后面乘的值并不是当前角度-机械中值,而是一个我们速度的期望。(这个理解了很重要!!!!)
a 1 = K p ∗ ( θ − a 2 ) + K d ∗ θ ′ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ① 直 立 环 a_1=Kp*(\theta-a_2)+Kd*\theta' \qquad········································①直立环 a1=Kp∗(θ−a2)+Kd∗θ′⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅①直立环
a 2 = K p 1 ∗ E r r s p e e d + K i 1 ∗ ∑ E r r s p e e d ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ② 速 度 环 a_2=Kp_1*Err_{speed}+Ki_1*\sum Err_{speed}\space \qquad·····························②速度环 a2=Kp1∗Errspeed+Ki1∗∑Errspeed ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅②速度环
合并一下就可以得到:
a = K p ∗ ( θ ) + K d ∗ θ ′ − K p [ k p 1 ∗ E r r s p e e d + k i 1 ∗ ∑ E r r s p e e d ] ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ③ 最 终 式 a=Kp*(\theta)+Kd*\theta'-Kp[kp_1*Err_{speed}+ki_1*\sum Err_{speed}] \qquad········③最终式 a=Kp∗(θ)+Kd∗θ′−Kp[kp1∗Errspeed+ki1∗∑Errspeed]⋅⋅⋅⋅⋅⋅⋅⋅③最终式
因此在代码实现上我们就可以实现两个环的直接相加或相减,在TIM3定时器中10ms一个周期进行控制。
Balance_PID_Result = Position_PID_Cal(&Balance_PID, imu.Roll + 0.3f);
if (Time_GAP_20ms) Velocity_PID_Result = Position_PID_Cal(&Velocity_PID, Velocity);
PID_Result = Balance_PID_Result + Velocity_PID_Result;
Set_Motor_Speed(PID_Result, PID_Result);
2.1.2 调参经验
根据上边的分析我们只需要分别调整直立环的Kp,kd和速度环的Kp,Ki
- 对于直立环的
Kp,是调整最方便观察现象的,太小时小车没有足够的恢复力,太大时小车会在中值附近大幅震荡,调整到一个略微震荡的值即可 - 直立环的
Kd作用是减小低频振荡,但Kd太大小车又会造成高频振动,从小到大增大Kd,直到小车出现小幅高频振荡 - 直立环调整结束后小车可以平衡,但受到扰动便会往一个方向疯跑,现在引入直立环
- 网上查到的资料对于速度环
Ki = Kp/200,但在我的实际调整中最终确定了Ki = Kp/100,这个看自己小车了,可以先按照Ki = Kp/200去调 - 先将直立环
Kp,Kd同时×0.8。调整速度环Kp,速度环Kp越大,小车便越不会出现向一个方向狂奔的情况(因为速度被速度环控住了),但会减弱直立环的控制效果,因此调整到一个车受到干扰会摇摇晃晃停下的一个状态。 - 摇摇晃晃的原因就是因为速度环
Kp太大,回调速度环Kp,并且增大直立环Kd(想想Kd的作用是什么呢?)
以上就是我调参的经验,可以参考,最好可以理解原理再去上手实践。
2.2 Mahony算法
参考一篇文章:基于Manony滤波算法的姿态解算
2.2.1 IMU(以MPU6050举例)
MPU6050是一个集成了陀螺仪和加速度计的传感器,它能输出在直角坐标系下的x,y,z轴的角速度和加速度数据。
陀螺仪输出的格式为:绕x轴的旋转角速度,绕y轴的角速度,绕z轴的角速度(分别称为roll角速度,pitch角速度和yaw角速度)。
加速度计输出的格式为:x轴的加速度,y轴的加速度,z轴的加速度。
另外还需要关注传感器的其他参数如:
- 陀螺仪的量程:
eg.±2000dps - 加速度计的量程:
eg.±2g -
ADC转换精度为16bit - 传感器采样率
4-1000hz:eg.1000hz
我们从IMU那就得到了陀螺仪数据gx,gy,gz,加速度数据az,ay,az
螺仪转换精度2^16=65536 , 65536/{2000-(-2000)}=16.4,实际1°等于ADC值16.4
采样率就是数据的更新率,也就是我们每次读取数据的频率。
首先将陀螺仪的数据转换成角度,这里封装成一个函数
2.2.2 算法实现
static void Get_IMU_Values(float *values)
{
int16_t gyro[3],acc[3];
IMU_readGyro_Acc(&gyro[0],&acc[0]);
for(int i=0;i<3;i++)
{
//gyro range +-2000; adc accuracy 2^16=65536; 65536/4000=16.4;
values[i]=((float) gyro[i])/16.4f;
values[3+i]=(float) acc[i];
}
}
然后编写函数实现计算姿态角的功能,使用四元数计算姿态角的公式在理论分析中推导:
其中α为绕x轴旋转角即roll,β为绕y轴旋转角即pitch,γ为绕z轴旋转角即yaw。a,b,c,d即q0,q1,q2,q3.
void IMU_Update(void)
{
static float q[4];
float Values[6];
Get_IMU_Values(Values);
//change angle to radian,the calculate the imu with Mahony
MahonyAHRSupdateIMU(Values[0] * PI/180, Values[1] * PI/180, Values[2] * PI/180,
Values[3], Values[4], Values[5]);
//save Quaternion
q[0] = q0;
q[1] = q1;
q[2] = q2;
q[3] = q3;
imu.ax = Values[3];
imu.ay = Values[4];
imu.az = Values[5];
imu.Pitch_v = Values[0];
imu.Roll_v = Values[1];
imu.Yaw_v = Values[2];
//calculate the imu angle with quaternion
imu.Roll = (atan2(2.0f*(q[0]*q[1] + q[2]*q[3]),1 - 2.0f*(q[1]*q[1] + q[2]*q[2])))* 180/PI;
imu.Pitch = -safe_asin(2.0f*(q[0]*q[2] - q[1]*q[3]))* 180/PI;
imu.Yaw = -atan2(2 * q1 * q2 + 2 * q0 * q3, -2 * q2*q2 - 2 * q3 * q3 + 1)* 180/PI;
}
代码中MahonyAHRSupdateIMU()函数实现的就是四元数的更新算法。
逻辑上,首先用加速度计校准陀螺仪,方式是通过计算当前四元数姿态下的重力分量,与加速度计的重力分量作叉积,得到误差。
对误差作P(比例)和I(积分)运算后加到陀螺仪角速度上。最终由角速度计算新的四元数。
代码中的 sampleFreq 即执行姿态解算的频率,这里用定时器,以500HZ的频率调用get_angle();
void MahonyAHRSupdateIMU(float gx, float gy, float gz, float ax, float ay, float az) {
float recipNorm;
float halfvx, halfvy, halfvz; //1/2 重力分量
float halfex, halfey, halfez; //1/2 重力误差
float qa, qb, qc;
//对加速度数据归一化
recipNorm = invSqrt(ax * ax + ay * ay + az * az);
ax *= recipNorm;
ay *= recipNorm;
az *= recipNorm;
// 由四元数计算重力分量
halfvx = q1 * q3 - q0 * q2;
halfvy = q0 * q1 + q2 * q3;
halfvz = q0 * q0 - 0.5f + q3 * q3;
// 将四元数重力分量 与 加速度计重力分量 作叉积 得到误差
halfex = (ay * halfvz - az * halfvy);
halfey = (az * halfvx - ax * halfvz);
halfez = (ax * halfvy - ay * halfvx);
//对误差作积分
integralFBx += twoKi * halfex * (1.0f / sampleFreq);
integralFBy += twoKi * halfey * (1.0f / sampleFreq);
integralFBz += twoKi * halfez * (1.0f / sampleFreq);
//反馈到角速度
gx += integralFBx; gy += integralFBy; gz += integralFBz;
// 对误差作比例运算并反馈
gx += twoKp * halfex; gy += twoKp * halfey; gz += twoKp * halfez;
// 计算1/2 dt
gx *= (0.5f * (1.0f / sampleFreq));
gy *= (0.5f * (1.0f / sampleFreq));
gz *= (0.5f * (1.0f / sampleFreq));
qa = q0; qb = q1; qc = q2;
// 更新四元数
q0 += (-qb * gx - qc * gy - q3 * gz);
q1 += (qa * gx + qc * gz - q3 * gy);
q2 += (qa * gy - qb * gz + q3 * gx);
q3 += (qa * gz + qb * gy - qc * gx);
// 四元数归一化
recipNorm = invSqrt(q0 * q0 + q1 * q1 + q2 * q2 + q3 * q3);
q0 *= recipNorm; q1 *= recipNorm; q2 *= recipNorm; q3 *= recipNorm;
}
由于加速度计对水平方向的旋转无能为力,故用此程序得到的yaw角数据会一直漂移,无法得到校准;通常的解决方法是增加一个磁场传感器,来获得一个准确的水平方向角来校准陀螺仪的漂移。MPU6050支持扩展一个IIC接口到磁场传感器,可通过配置MPU6050的IIC MASTER 来读取磁场传感器的数据。
在Mahony中提供了包含磁场数据的融合函数:
> void MahonyAHRSupdate(float gx, float gy, float gz, float ax, float ay, float az,
> float mx, float my, float mz);
3. 程序逻辑
首先看main函数:
int main(void)
{
All_HardWare_init();
while (1)
{
Protect_Check();
LED_show_working();
LCD_show_Brief_info();
}
}
代码都封装在了函数里,因此主控的main函数非常简单。All_HardWare_init();包含了所有硬件、片内资源的初始化。因为Mahony每次上电融合解算姿态时需要几秒的自我校准,因此先打开定时器。
TIM3_Int_Init(99, 7199); // 72M ÷7200 ÷100 = 10 ms
几秒过后再初始化PID控制器
PID_init(); //直立环,速度环PID控制器初始化
定时器3中断服务函数在control.c文件中,包含姿态解算和PID控制。
void TIM3_IRQHandler(void)
{
if (TIM_GetITStatus(TIM3, TIM_IT_Update) == SET)
{ TIM_ClearITPendingBit(TIM3, TIM_IT_Update);
/**
*PID控制与姿态解算部分,详情请TP至
*....../主控程序/HARDWARE/control/control.c
*
*/
}
}
死循环中目前三个函数分别是LED、LCD状态显示和 一个简易的过倾保护。文章来源:https://www.toymoban.com/news/detail-401890.html
void Protect_Check(void)
{
if (imu.Roll > 30 || imu.Roll < -30)
Protect = 1;
else
Protect = 0;
}
4. 补充
还在更新,会做出更多的功能文章来源地址https://www.toymoban.com/news/detail-401890.html
到了这里,关于STM32平衡车的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!