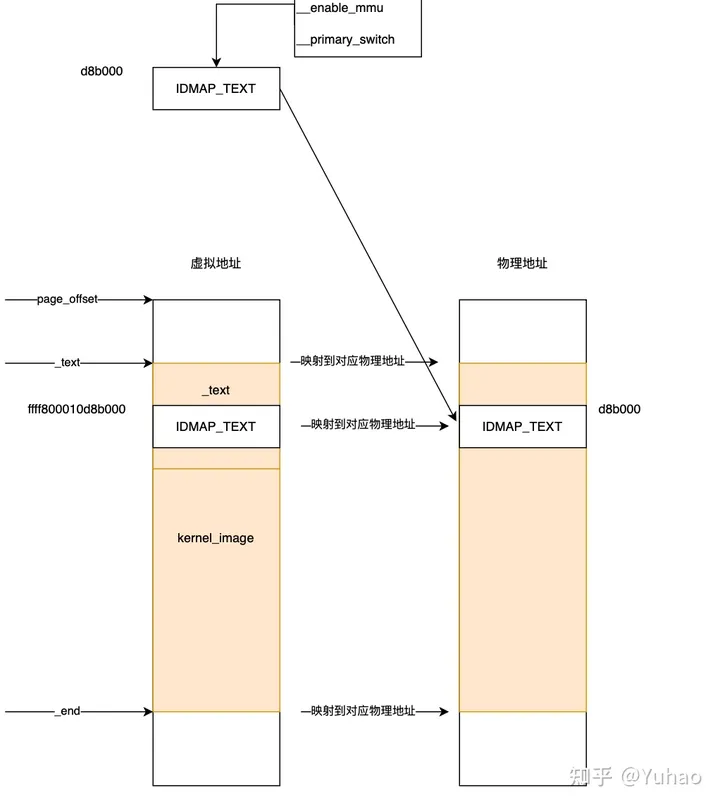
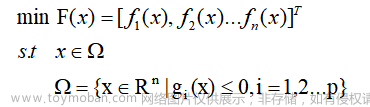NSGA-II改进之种群初始化-Toy模板网

这篇具有很好参考价值的文章主要介绍了NSGA-II改进之种群初始化。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

原NSGA-II的算法在初始化种群的时候采用的是随机生成。随机代表着不确定，且随机生成的种群在整个空间上表现为不均匀；为消除随机初始化带来的不确定，和种群在空间上分布不均匀问题，由此引出新的初始化种群方式：佳点集生成种群

注：种群的初始化结果是否对种群的进化是否有影响，个人并没有做太大的研究，仁者见仁智者见智。

1-什么是佳点集

佳点集最初是由华罗庚等提出，基本定义和构造为：
$\begin{aligned} &假设Gs是s维的欧式几何空间，那么r\in Gs,那么P_n(i)=(r_1i_i,r_2i_2,r_3i_3,...r_ni_n),i=1,2,3,...n。 \\&n表示样本数量，P_n(i)表示佳点集，而r指的是佳点，一般取 r=\begin{Bmatrix} 2cos(\frac{2\pi j}{k})i, 1\leq i\leq n;1\leq j\leq s \end{Bmatrix} 或者取 \\&r=\begin{Bmatrix} e^ji \end{Bmatrix}。其中k是满足( k − 3 ) / 2 ≥ 的最小素数。 \end{aligned}$

2-佳点集初始化种群的方法

已知：种群所在的空间维度为n，种群数量为m

$\begin{aligned} &step1:计算r值，r=(r_1,r_2,...r_n),其中r_j=mod(2cos(\frac{2\pi j}{7})m_i,1),1\leq j\leq n。m_i表示第i个个体\\ \\&step2：构造数量m的佳点集： \\& P_n(i)=\begin{Bmatrix} (r_1i_1,r_2i_2,...r_ni_n) \end{Bmatrix} ,i=1,2,3,...n\\ \\&step3:将P_n映射到种群所在的可行域上：\\ &X_i^j=a_j+P_n(i)(b_j-a_j) \\&其中a_j表示当前维度的下限，b_j表示当前维度的上限 \end{aligned}$

3-佳点集初始化种群与随机初始化种群的对比

假设种群规模为100

佳点集生成

随机生成

4-佳点集初始化种群代码（matlab）

% pop_size：种群数量
% dimension：维度
% bound：取值范围
function pop = init_pop(pop_size,dimension,bounds)
%佳点集生成初始种群
p = zeros(pop_size,dimension);
prime_number_min = dimension*2 +3;
% 找到(prime_number_min-3)/2>=dimension的最小素数prime_number_min
while 1
    if isprime(prime_number_min)==1
        break;
    else
       prime_number_min = prime_number_min + 1;
    end
end

for i = 1:pop_size
    for j = 1:dimension
        r = mod(2*cos(2*pi*j/prime_number_min)*i,1);% 对应维度的r
%         r = mod(exp(j)*i,1);
        p(i,j) = bounds(j,1)+r*(bounds(j,2)-bounds(j,1));
    end
end
pop = p;
end

% %随机i生成定义域范围内种群
% p = rand(pop_size,dimension);%生成popsize*dimension的0-1矩阵
% for i = 1:dimension
%     p(:,i) = bounds(i,1)+p(:,i)*(bounds(i,2)-bounds(i,1));
% end

5-画图对比

function test_plot_pop()
% 分别画出2维，3维情况下采用佳点集和随机生成图的对比
% 定于种群大小
pop_size = 100;
% 定义种群的取值范围 
dimension_2 = 2;
dimension_3 = 3;
bounds_2 = [ones(dimension_2,1)*0,ones(dimension_2,1)*1];
bounds_3 = [ones(dimension_3,1)*0,ones(dimension_3,1)*1];
% 二维、三维的佳点集种群
pop2 = init_pop(pop_size,dimension_2,bounds_2);
pop3 = init_pop(pop_size,dimension_3,bounds_3);
% 二维、三维随机生成的种群
pop2_rand = init_pop_rand(pop_size,dimension_2,bounds_2);
pop3_rand = init_pop_rand(pop_size,dimension_3,bounds_3);

% 画出二维下图形佳点集种群，和随机种群
subplot(2,2,1)
plot(pop2(:,1),pop2(:,2),'*')
subplot(2,2,2)
plot(pop2_rand(:,1),pop2_rand(:,2),'*')
subplot(2,2,3)
plot3(pop3(:,1),pop3(:,2),pop3(:,3),'*')
subplot(2,2,4)
plot3(pop3_rand(:,1),pop3_rand(:,2),pop3_rand(:,3),'*')
end

%%
% pop_size：种群数量
% dimension：维度
% bound：取值范围
function pop = init_pop(pop_size,dimension,bounds)
%佳点集生成初始种群
p = zeros(pop_size,dimension);
prime_number_min = dimension*2 +3;
% 找到(prime_number_min-3)/2>=dimension的最小素数prime_number_min
while 1
    if isprime(prime_number_min)==1
        break;
    else
       prime_number_min = prime_number_min + 1;
    end
end

for i = 1:pop_size
    for j = 1:dimension
        r = mod(2*cos(2*pi*j/prime_number_min)*i,1);% 对应维度的r
%         r = mod(exp(j)*i,1);
        p(i,j) = bounds(j,1)+r*(bounds(j,2)-bounds(j,1));
    end
end
pop = p;
end
%%
function pop = init_pop_rand(pop_size,dimension,bounds)
%随机i生成定义域范围内种群
p = rand(pop_size,dimension);%生成popsize*dimension的0-1矩阵
for i = 1:dimension
    p(:,i) = bounds(i,1)+p(:,i)*(bounds(i,2)-bounds(i,1));
end
pop = p;
end