彻底搞懂图的深度优先算法(Debug+图解+JavaDOC)-Toy模板网

这篇具有很好参考价值的文章主要介绍了彻底搞懂图的深度优先算法(Debug+图解+JavaDOC)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

深度优先算法

从算法的思想,算法步骤,代码实现与分析,最后"debug+图解"展示展开

会有一定的图示,以便于更好的理解(博主的自我思考,如有错误,欢迎指正)

需要源码与相关图解请评论区留言

博客空间https://blog.csdn.net/JOElib?spm=1011.2266.3001.5343文件压缩与解压https://blog.csdn.net/JOElib/article/details/123965081?spm=1001.2014.3001.5501排序算法https://blog.csdn.net/JOElib/article/details/123623176?spm=1001.2014.3001.5501

算法思想🐼

算法步骤🐼

DOC注释🐼

代码实现(核心代码)🐼

1.创建寻找第一个邻接节点的方法🐻

代码分析:🐨

2.创建寻找后一个邻接节点的方法🐻

代码分析:🐨

3.创建核心DFS(深度优先搜索)的方法🐻

代码分析:🐨

4.对DFS进行重载🐻

代码分析:🐨

DeBug与图解🐼

结论:

算法思想🐼

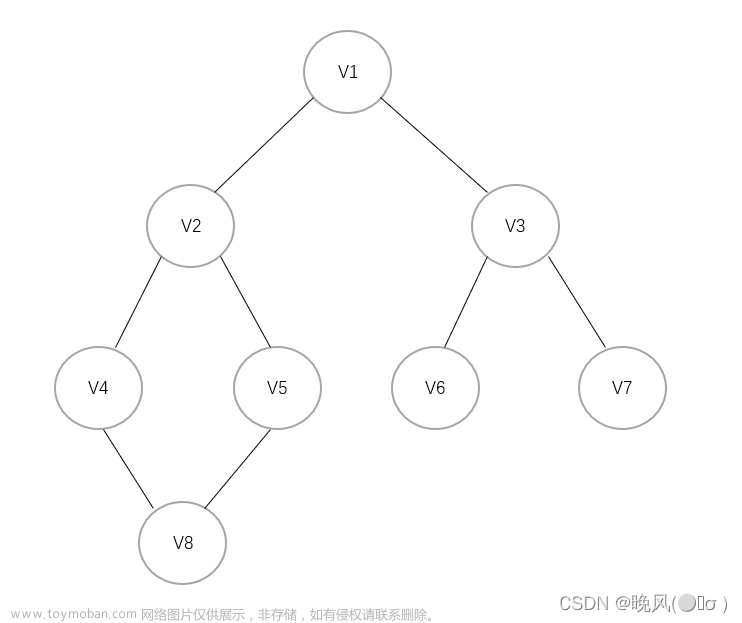
从访问初始节点出发,访问初始节点可能有很多个邻接节点,深度优先算法的策略是首先访问第一个邻接节点,然后再以这个被访问的邻接节点作为访问初始节点,接着访问他的第一个邻接节点
即:每次访问完当前节点首先访问当前节点的第一个邻接节点
不难看出,访问策略往纵向发掘深入,而不是对一个节点的所有邻接节点进行访问
显然,深度优先搜索算法是一个递归的过程

算法步骤🐼

访问初始节点v,并将该节点标记为已读
查找初始节点的第一个邻接节点w
如果邻接节点w存在,则执行4,若不存在,则返回-1,从v的下一个未访问的节点继续
若w未被访问,对w进行深度优先搜索递归(即把w当作另一个v,然后再进行123)
若w被访问,查找节点v的w的下一个邻接节点,转到3

DOC注释🐼

彻底搞懂图的深度优先算法(Debug+图解+JavaDOC)

请认真查阅Javadoc注释,否则无法看得懂下面的代码的目的

代码实现(核心代码)🐼

1.创建寻找第一个邻接节点的方法🐻

public int getFirstVertex(int index) {
        for (int i = 0; i < vertexList.size(); i++) {
            if (edges[index][i] > 0) {
                return i;
            }
        }
        return -1;
    }

代码分析:🐨

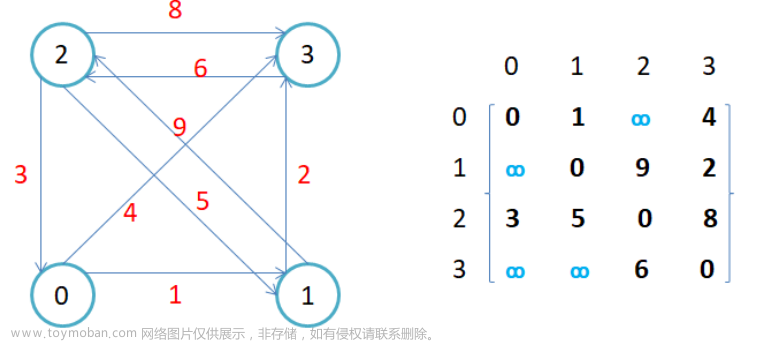
通过邻接矩阵我们就可以得到各节点之间边的权值,根据权值我们就可以得到其邻接节点,故,我们需要用到邻接矩阵这个二维数组
for循环的详解:
1. i初始化为0的目的是:"找到第一个邻接节点"这句话得出,为了保证第一,所以要从下标为0的元素开始遍历
2. i<vertexList.size()的目的是:在元素内遍历,防止空指针异常;即,将所有的元素遍历一遍
3. 如果edges[index][i] > 0,说明有边,为当前下标元素的邻接节点,返回该节点下标
如果循环后没有返回任何数据,说明该节点没有任何邻接节点,直接返回-1

2.创建寻找后一个邻接节点的方法🐻

public int getVertexByLast(int v1,int v2) {
        for (int i = v2 + 1; i < vertexList.size() ; i++) {
            if (edges[v1][i] > 0) {
                return i;
            }
        }
        return -1;
    }

代码分析:🐨

方法说明:该方法本质意思是找到当前节点的下一个邻接节点(如:JKL是他的邻接节点,第一次找到J,则调用该方法就会找到K)
for循环的详解
1. i = v2+1,其原因是"找到下一个邻接节点",如果将i赋值为v2,v2就是v1的一个邻接节点,直接返回,造成死循环,所以,找到他下一个邻接节点至少从他的下一个位置开始,切必须从该位置开始
2. i<vertexList.size()的目的是:在元素内遍历,防止空指针异常;即,将所有的元素遍历一遍
同理方法1后面的几句话

3.创建核心DFS(深度优先搜索)的方法🐻

该方法严格遵守算法步骤执行

private void dfs(boolean[] isVisited,int v) {
        System.out.println(getItem(v));
        isVisited[v] = true;
        var w = getFirstVertex(v);
        while (w != -1) {
            if (!isVisited[w]) {
                dfs(isVisited, w);
            }
            w = getVertexByLast(v,w);
        }
        dfs();
    }

代码分析:🐨

先输出当前节点对应的数据
并将该节点标记成已读
获取当前节点的第一个邻接节点
若该邻接节点存在,则进入循环
若该邻接节点未被读取,则递归进入,继续进行DFS(深度优先)
否则找到下一个邻接节点,继续判断是否被读取
如果该邻接节点不存在,则寻找下一个未被读取的节点

4.对DFS进行重载🐻

@First("The DFS should be firstly invoked")
public void dfs() {
        for (int i = 0; i < vertexList.size(); i++) {
            if (!isVisited[i]) {
                dfs(isVisited,i);
            }
        }
}

代码分析:🐨

该方法的目的是:寻找一个未被读取的节点,为了方便算法,我们默认从下标为0的节点开始
如果未被读取,则调用3方法,这个方法就实现了算法找不到邻接节点时所需要的操作

DeBug与图解🐼

彻底搞懂图的深度优先算法(Debug+图解+JavaDOC)

彻底搞懂图的深度优先算法(Debug+图解+JavaDOC) 同理得出"C"第一次找到的邻接节点是"A",第二次是"B",直到这一步

彻底搞懂图的深度优先算法(Debug+图解+JavaDOC)

彻底搞懂图的深度优先算法(Debug+图解+JavaDOC) debug结束,剩余的逻辑与以上的逻辑一致,相信友友们可以自行解决

结论:

DFS算法比较抽象,不知道这种讲述方式大家能否可以接受,我来总结一下必须要掌握的几点:

1.算法步骤如何进行

2.算法思想如何理解(重点理解为什么是纵向深入)

3.算法如何构建

🚇下一站:图的广度优先算法文章来源地址https://www.toymoban.com/news/detail-402396.html

到了这里，关于彻底搞懂图的深度优先算法(Debug+图解+JavaDOC)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！