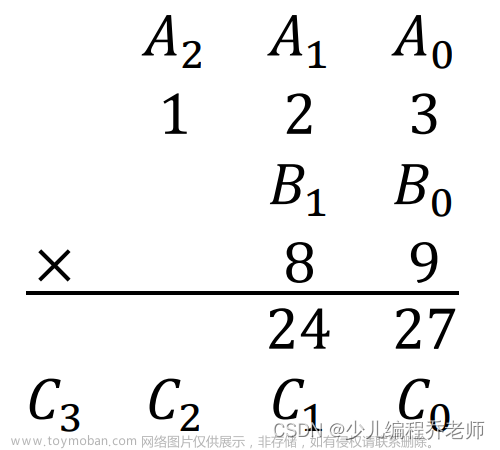📖作者介绍:22级树莓人(计算机专业),热爱编程<目前在c++阶段,因为最近参加新星计划算法赛道(白佬),所以加快了脚步,果然急迫感会增加动力>——目标Windows,MySQL,Qt,数据结构与算法,Linux,多线程,会持续分享学习成果和小项目的
📖作者主页:热爱编程的小K
📖专栏链接:算法笔记🎉欢迎各位→点赞👏 + 收藏💞 + 留言🔔
💬总结:希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🐾

✨一、高精度算法的应用场景
利用计算机进行数值计算,有时会遇到这样的问题:有些计算要求精度高,希望计算的数的位数可达几十位甚至几百位,虽然计算机的计算精度也算较高了,但因受到硬件的限制,往往达不到实际问题所要求的精度。我们可以利用程序设计的方法去实现这样的高精度计算。这里不包括java和Python选手哈,当输入很大的时候
scanf比cin效率更高
✨二、高精度加法
1、思路
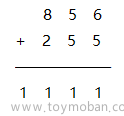
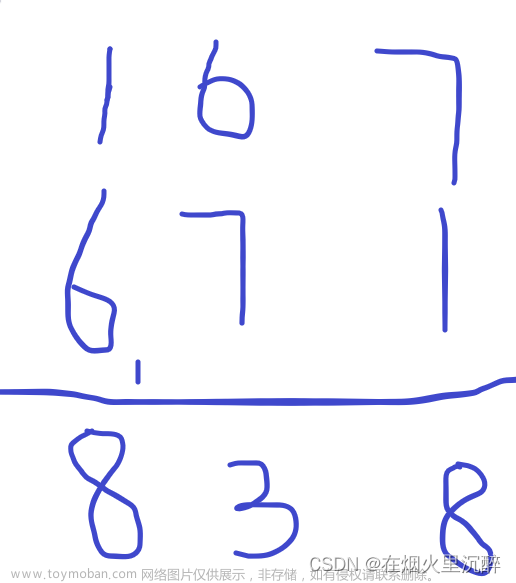
我们先手动模拟一下加法
先个位相加:6+6=12,所以个位的结果得2,向十位进1
再十位相加:6+9+1(进位)=16,所以十位的结果得6,向百位进1
最后再百位相加:5+1(进位)=6,所以百位的结果得6,进位为0
2、算法
第一步:需要把两个大整数倒序过来储存到一个数组中,因为我们都知道加法是从低位开始加的
第二步:判断较长的数字,放在前面,因为循环条件需要
第三步:开始计算
A[i]+B[i]+t这里t表示进位,前面的和表示为sum,则当前的位的结果表示为sum%10,进位更新t/=10循环结束后:判断t为不为0,如果不为0,需要把t存到和数组中(这种情况就是和比最长加数还要长的情况)
3、模板展示
vector<int> add(vector<int> &A, vector<int> &B)
{
if (A.size() < B.size()) return add(B, A);
//为了方便计算,让A中保存较长的数字, B中保存较短的数字
vector<int> C;//保存结果的数组
int t = 0;//进位,开始时是0
for (int i = 0; i < A.size(); i ++ )//依次计算每一位
{
t += A[i];//加上 A 的第 i 位上的数字
if (i < B.size()) t += B[i];//加上 B 的第 i 位上的数字
C.push_back(t % 10); //C 中放入结果
t /= 10;//t 更新成进位
}
if (t) C.push_back(t);//最后如果进位上有数,放进结果数组
return C;//返回结果
}
💖4、习题练习
1、题目:Acwing 791. 高精度加法
给定两个正整数(不含前导 0),计算它们的和。
输入格式
共两行,每行包含一个整数。
输出格式
共一行,包含所求的和。
数据范围
1≤整数长度≤100000
输入样例:
12
23
输出样例:
35
2、代码展示
#include<iostream>
#include<string>
#include<vector>
using namespace std;
vector<int> add(vector<int>&A,vector<int>&B)
{
vector<int> C;
if(A.size()<B.size()) return add(B,A);//大的放前面,判断
int t=0;//进位
for(int i=0;i<A.size();i++)
{
t+=A[i];
if(i<B.size()) t+=B[i];
C.push_back(t%10);
t/=10;
}
if(t) C.push_back(t);
return C;
}
int main()
{
string a,b;
vector<int> A,B;
cin>>a>>b;
//倒序存放
for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
for(int i=b.size()-1;i>=0;i--) B.push_back(b[i]-'0');
auto C=add(A,B);
for(int i=C.size()-1;i>=0;i--) cout<<C[i];
cout<<endl;
return 0;
}
✨三、高精度减法
1、思路
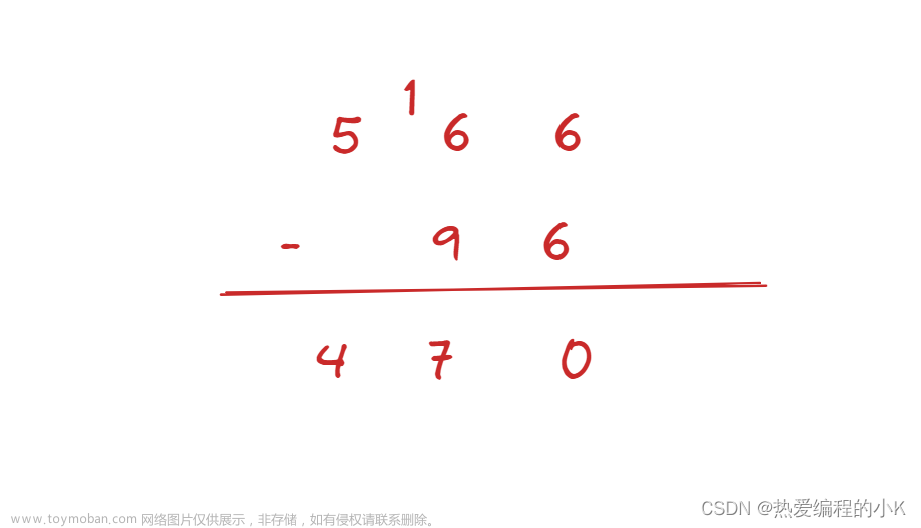
一样的我们先模拟一下减法竖式:
- 和高精度加法差不多,值得注意的是
- 减法的借位处理
- 相减为负数的处理
- 前导0的处理
2、算法
- 对于两个减数的处理
t = A[i] - B[i] - t;可以拆为t = A[i] - t如果B[i]合法,再t -= B[i]这么两步来做,这里的t表示借位- 两数对应位置相减后放入的应为
(t+10)%10,解释:t>0时,对应位的结果就为t,t<0时,对应结果为t-10,借位- 相减为负数的处理:加一个判断大小的函数,大的当减数,小的当被减数,为负的情况最后再输出的时候再先输出一个负号
3、模板展示
vector<int> sub(vector<int>&A,vector<int>&B)
{
vector<int> C;
int t=0;
for(int i=0;i<A.size();i++)
{
t=A[i]-t;
if(i<B.size()) t-=B[i];
C.push_back((t+10)%10);
//借位处理
if(t<0) t=1;
else t=0;
}
//前导0处理
while(C.size()>1&&C.back()==0) C.pop_back();
return C;
}
💖 4、习题练习
1、题目 Acwing 792. 高精度减法
给定两个正整数(不含前导 00),计算它们的差,计算结果可能为负数。
输入格式
共两行,每行包含一个整数。
输出格式
共一行,包含所求的差。
数据范围
1≤整数长度≤10的5次方
输入样例:
32
11
输出样例:
21
2、代码展示
#include <iostream>
#include <vector>
using namespace std;
bool cmp(vector <int> &A,vector <int> &B)
{
// 判断是否A > B
if(A.size() != B.size()) return A.size() > B.size();
// 如果A、B长度不相同,长度长的那个数大
for(int i = A.size() - 1;i >= 0;i --)
{
// 否则就要从最高位开始看(因为执行这个函数前,A和B数组都已经倒序,所以这里要从后往前看)
if(A[i] != B[i]) return A[i] > B[i];
// 如果A的当前位和B的当前位不相等,当前位大的更大
}
return true; // 如果A、B数组都相等,这里可以直接返回true,当然也可以直接输出0
}
vector <int> sub(vector <int> &A,vector <int> &B)
{ // A - B
int t = 0; // 每一位上相减得到的数
vector <int> C; // 最后的答案
// 遍历一遍,和高精度加法不一样的是,只要遍历完A就行了,因为这里A肯定比B长
for(int i = 0;i < A.size();i ++)
{
t = A[i] - t;// t要等于A的当前位减掉自己,因为上一位有可能出现借位的情况
if(i < B.size()) t -= B[i]; // 如果没有遍历完B,那么t减掉B的当前位
C.push_back((t + 10) % 10);
// 更新C数组
// 这里如果没有借位,(t + 10) % 10就刚好等于t
// 如果这里有借位,(t + 10) % 10就会借一个10下来
if(t < 0) t = 1;
// 如果t < 0,说明不够减,需要借位,把t赋值为1,就是在下一次执行中,A的当前位会减掉t
else t = 0; // 否则够减,赋值为0,不用借位
}
while(C.size() > 1 && C.back() == 0) C.pop_back(); // 删除前导0
return C; // 返回答案
}
int main(){
string a,b; // 两个数,因为很大,所以用string来存
cin>>a>>b; // 读入
vector <int> A,B; // 两个数,因为减法是从最低位开始减,我们可以把两个数倒过来
for(int i = a.size() - 1;i >= 0;i --) A.push_back(a[i] - '0');
// 把a数组到过来存入A,记得a是string类型的数组,要减去'0'让它变成数字
for(int i = b.size() - 1;i >= 0;i --) B.push_back(b[i] - '0');
// 把b数组倒过来存入B
if(cmp(A,B))
{
// 如果A > B
auto C = sub(A,B); // 那么可以直接相减
for(int i = C.size() - 1;i >= 0;i --) printf("%d",C[i]);
// 最后因为C是倒着的,需要反向输出
}
else
{ // 否则A < B,需要计算-(B - A)
auto C = sub(B,A); // 计算B - A
printf("-"); // 给前面加上一个负号
for(int i = C.size() - 1;i >= 0;i --) printf("%d",C[i]); // 反向输出C数组
}
return 0;
}
✨四、高精度乘法
高精度乘法就没什么好说的,直接上习题,代码有讲解
💖1、题目 Acwing 793. 高精度乘法
给定两个非负整数(不含前导 0)A和 B,请你计算 A×B 的值。
输入格式
共两行,第一行包含整数 A,第二行包含整数 B。
输出格式
共一行,包含 A×B 的值。
数据范围
1≤A的长度≤100000
0≤B≤100000
输入样例:
2
3
输出样例:
6
2、代码展示
#include<iostream>
#include<string>
#include<vector>
using namespace std;
vector<int> mul(vector<int>&A,int b)
{
vector<int> C;
int t=0;//进位
//A的长度一定比b长,而且这里加了`||t`
for(int i=0;i<A.size()||t;i++)
{
if(i<A.size()) t+=A[i]*b;
C.push_back(t%10);
t/=10;
}
//去除前导0
while(C.size()>1&&C.back()==0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin>>a>>b;
vector<int> A;
//倒序
for(int i=a.size()-1;i>=0;i--) A.push_back(a[i]-'0');
auto C=mul(A,b);
for(int i=C.size()-1;i>=0;i--) cout<<C[i];
return 0;
}
✨五、高精度除法
1、模拟与算法
我们先模拟一下
需要注意的就两点:第一个:余数
r传入函数的时候一定要传入引用,因为要修改并返回r的值第二个:上一位的余数乘以10,再加上当前位上的数就是余数
💖2、题目 Acwing 794. 高精度除法
给定两个非负整数(不含前导 00) A,B,请你计算 A/B的商和余数。
输入格式
共两行,第一行包含整数 A,第二行包含整数 B。
输出格式
共两行,第一行输出所求的商,第二行输出所求余数。文章来源:https://www.toymoban.com/news/detail-402599.html
数据范围
1≤A的长度≤100000
1≤B≤10000
B不一定不为 0文章来源地址https://www.toymoban.com/news/detail-402599.html
输入样例:
7
2
输出样例:
3
1
3、代码展示
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector <int> div(vector <int> &A,int b,int &r)
{
// 取r的地址符,是为了更改r的值,方便后面输出余数
vector <int> C; // 答案
r = 0; // 余数
for(int i = A.size() - 1;i >= 0;i --)
{
// 从最高位开始处理
r = r * 10 + A[i]; // 上一次的余数乘10,再加上当前位上的数,就是被除数
C.push_back(r / b); // 往C里压入这个被除数除b
r %= b; // 计算余数
}
reverse(C.begin(),C.end());
// 因为除法运算中从高位开始计算,而前导0都在顶部而不是底部,所以要翻转过来
while (C.size() > 1 && C.back() == 0) C.pop_back(); // 去除前导0
return C; // 返回答案
}
int main()
{
string a;
int b;
cin>>a>>b;
vector <int> A;
for(int i = a.size() - 1;i >= 0;i --) A.push_back(a[i] - '0'); // 倒序
int r;
auto C = div(A,b,r); // 答案
for(int i = C.size() - 1;i >= 0;i --) cout<<C[i];
cout<<endl<<r<<endl;
return 0;
}
到了这里,关于算法笔记——高精度算法(附源码)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!