1.Identify which of the following equations are linear equations:
（判断哪些是线性方程）
只有（4）是，一般形式如下
特征：每一项都是一次的，也不代幂什么的
线性方程组（System of linear equations）
ai,j是系数（i代表是第几个方程里，j是代表在方程里的第几个），b1是右端项，xj是未知量
一个数带入后使方程组中的每个方程都成立，那个数叫做方程组的解
线性方程组解集的几何解释
2x2线性方程组
从几何角度来看，每个方程的解集可以用平面上的直线表示。根据这个几何解释，我们确定有三种可能性：
（1）两条直线重合成一条直线，所以会有无限的解
（2）两条直线是平行的，所以它们永远不会相交，所以解不存在。
（3）两条直线相交于一点，所以有一个唯一的解。
2x3线性方程组(对于m*n的方程组，m小于n时只有这两种情况)
(1)两个平面以一条直线重合或相交。在这种情况下，系统有无限的解。
(2)两个平面是平行的。在这种情况下，该系统的解决方案并不存在。
3*3的线性方程组
只要两个平面平行就是无解
定义1.1如果两个具有n个未知变量的线性方程组具有相同的解集，我们说它们是等价的系统。
线性方程组的求解
1.化简方程 2.求解化简后的方程得到原方程的解
线性方程组的三种初等变换
（1）交换两个方程的位置
（2）将一个方程乘以一个非零常数
（3）将一个方程的常数乘以另一个方程
例题： 求解线性方程组（下面这个也叫阶梯型线性方程组）
上面这种用初等变换简化了系统，并进一步推导出了解。这种方法称为高斯消元法。
矩阵（Matrices）
矩阵是一个有m行和n列的矩形数字表，它由数字组成。
字母的下角标第一个数字表示行（row），第二个数字表示列（column）
特殊矩阵
只有一行的矩阵称为行矩阵。只有一列的矩阵称为列矩阵。
A=(1 4 5 2) 行矩阵
如果行数和列数相同，那么被称为n阶矩阵或n阶方阵，写成An
在n阶矩阵中，从左上角到右下角，n个项被称为的对角项。一个所有对角线项都是1，而其他所有项都是0的n阶矩阵被称为n阶单位矩阵，写成In或I
一个所有项都为0的矩阵被称为零矩阵，写成O。当它是行矩阵或列矩阵时，它也可以被写成0。
具有上面（或下面）对角项为0的矩阵称为上三角矩阵（或下三角矩阵）。
所有项都为0的矩阵称为对角矩阵
通常，我们用下面符号来描述一个带有对角项的n阶对角矩阵
线性方程的矩阵解释
A是系数矩阵
B是增广矩阵
矩阵的初等变换
（1）交换两个方程的位置。
（2）将一个方程乘以一个非零常数。
（3）将一个方程的常数倍数加到另一个方程中。
矩阵的基本变换
矩阵的基本行变换（基本列变换）
（1）交换两行（或列）的位置。
（2）将一行（或列）的项乘以一个非零常数。
（3）将一行（或列）项的常数倍数添加到相应位置的另一行（或列）。
阶梯形矩阵
（1）仅包含0的行（零行）位于矩阵的底部；
（2）如果(i+1)行有非零项，则第一个非零项在第i行的第一个非零条目的右侧。
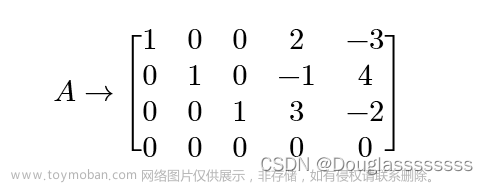
简化的阶梯型矩阵
如果梯队矩阵中每个非零行的第一个非零项（领先的非零项）为1，并且这个1上面和下面的项为0则称为简化梯队矩阵 。
简化的阶梯型矩阵和阶梯矩阵的区别
对于简化的阶梯形矩阵，矩阵的每一个非零行的领先非零项为1，上面和下面的项为0。
将阶梯矩阵变化为简化的阶梯矩阵
（1）查找包含非零条目目的第一列。
（2）如果需要，将第一行与另一行交换，以确保第一行的第一个非零项。
（3）如果a表示第一行的前导非零条目，则让第一行的每个条目都乘以1/a（这样，第一行的前导非零条目为1）。
（4）将第一行中的条目的适当时间添加到其他每行中，以确保第一行中前导项1下面的所有条目都为0。
（5）忽略第一行，对其余行重复步骤1到步骤4，直到该矩阵以阶梯形矩阵的形式出现。
（6）在我们得到一个阶梯形矩阵之后，我们应用从下到上的变换。将下非零行中的项的适当时间添加到其他行，以确保下行中前导项1以上的所有项都为0。
例子：
利用简化的阶梯矩阵求解线性方程组步骤：
（1）写出线性方程组的增广矩阵。
（2）将增广矩阵简化为一个简化的梯形矩阵。
（3）写出由简化的阶梯形矩阵表示的线性方程组。
（4）求解简化的线性方程组，得到原系统的解。
例子：
第一步：所给定系统的增广矩阵为
第二步：通过基本行变换将B变换为简化的梯队矩阵：
第三步：由最后一个简化梯队矩阵表示的线性方程组为
第四步：解出答案文章来源：https://www.toymoban.com/news/detail-402674.html
文章来源地址https://www.toymoban.com/news/detail-402674.html
到了这里，关于线性代数——线性方程组和矩阵（Linear and Matrices）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
