数学建模之熵权法（EWM）matlab实例实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了数学建模之熵权法（EWM）matlab实例实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

本文参考http://blog.sina.com.cn/s/blog_710e9b550101aqnv.html

熵权法是一种客观赋值的方法，即它通过数据所包含的信息量来确定权重，形象的说如果每个人考试都能考100分，那么这个指标对于这些人的评价是毫无意义的，因为没有任何区分度，熵权法就是通过区分度来确定对于特征的权值，从而能够对事物进行综合的评价。

一般来说，若某个指标的信息熵指标权重确定方法之熵权法越小，表明指标值得变异程度越大，提供的信息量越多，在综合评价中所能起到的作用也越大，其权重也就越大。相反，某个指标的信息熵指标权重确定方法之熵权法越大，表明指标值得变异程度越小，提供的信息量也越少，在综合评价中所起到的作用也越小，其权重也就越小。

基于此熵权法步骤如下：

首先需要将数据标准化即让数据分布在0-1之间，方式有多种
例如归一化，即当前特征元素-当前特征列的最小值/当前特征列的最大值-当前特征列的最小值（本文采用此方法）：
数学建模之熵权法（EWM）matlab实例实现
或者标准化

然后计算各指标的信息熵
pij表示的是当前元素在当前特征列的占比
Ej代表此特征的信息熵
且规定0ln0 = 0
数学建模之熵权法（EWM）matlab实例实现

最后就是确定各指标的权重
由于信息熵越大，其所代表的数据不确定性越大
因此信息熵越小，代表其区分度越高，即说明此特征越重要
因此需要1-Ei来获取对应特征的实际重要程度
再通过除以所有特征重要程度之和，即能计算出，此特征在所有特征中的重要程度占比，从而计算出对应特征的权重。
数学建模之熵权法（EWM）matlab实例实现

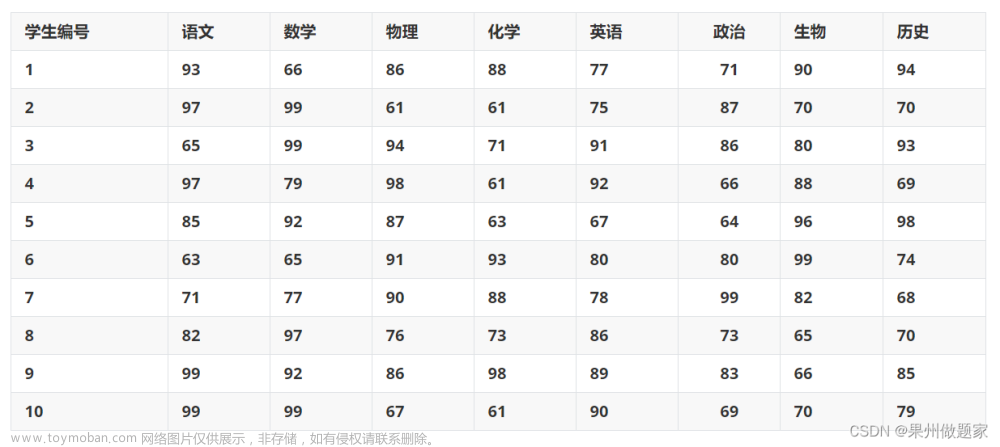
下边展示一道例题：
数学建模之熵权法（EWM）matlab实例实现
由于从题目中能够看出，各指标都是正向指标，因此最终特征值*特征权重求和也都是包含正向因素，值越大代表评价越高，但是如果包含负向评价的话，我认为，可能特征值取反应该就能转变成正向评价了吧。

第一步先进行归一化处理

data = [100,90,100,84,90,100,100,100,100
    100,100,78.6,100,90,100,100,100,100
    75,100,85.7,100,90,100,100,100,100
    100,100,78.6,100,90,100,94.4,100,100
    100,90,100,100,100,90,100,100,80
    100,100,100,100,90,100,100,85.7,100
    100,100,78.6,100,90,100,55.6,100,100
    87.5,100,85.7,100,100,100,100,100,100
    100,100,92.9,100,80,100,100,100,100
    100,90,100,100,100,100,100,100,100
    100,100,92.9,100,90,100,100,100,100];
[Y,PS] = mapminmax(data',0,1);%由于此函数是按行进行归一化的，因此先转置再转回来就好了
to_one = Y';

结果如下：
数学建模之熵权法（EWM）matlab实例实现
第二步求特征元素占比

ele_weight = [];
sum_col = sum(to_one); %默认按列求和
[row, col] = size(to_one); %获取原数据矩阵的行和列
for i = 1:row
    for j = 1:col
        ele_weight(i,j) = to_one(i,j)/sum_col(j); %计算出归一化后每个元素在所在特征列的占比
    end
end

第三步求各元素信息熵
数学建模之熵权法（EWM）matlab实例实现

E_ele = [];
for i = 1:row
    for j = 1:col
        if ele_weight(i,j) == 0 %规定0*ln(0) = 0,不赋值默认为0
            continue
        end
        E_ele(i,j) = -ele_weight(i,j)*log(ele_weight(i,j));%计算信息熵,matlab中log即取ln
    end
end
E = sum(E_ele./log(row));%计算此特征的信息熵
sum_E = sum(E)

最后一步通过特征信息熵求出特征权重并计算分数
数学建模之熵权法（EWM）matlab实例实现

W = (1-E)./(col-sum_E);%通过信息熵计算对应特征的权重，列数即为特征数
W = W';%转置便于矩阵乘法直接计算出对应的评价分数

data * W

matlab完整代码如下：文章来源地址https://www.toymoban.com/news/detail-402735.html

clc,clear
data = [100,90,100,84,90,100,100,100,100
    100,100,78.6,100,90,100,100,100,100
    75,100,85.7,100,90,100,100,100,100
    100,100,78.6,100,90,100,94.4,100,100
    100,90,100,100,100,90,100,100,80
    100,100,100,100,90,100,100,85.7,100
    100,100,78.6,100,90,100,55.6,100,100
    87.5,100,85.7,100,100,100,100,100,100
    100,100,92.9,100,80,100,100,100,100
    100,90,100,100,100,100,100,100,100
    100,100,92.9,100,90,100,100,100,100];
[Y,PS] = mapminmax(data',0,1);%由于此函数是按行进行归一化的，因此先转置再转回来就好了
to_one = Y';

ele_weight = [];
sum_col = sum(to_one); %默认按列求和
[row, col] = size(to_one); %获取原数据矩阵的行和列
for i = 1:row
    for j = 1:col
        ele_weight(i,j) = to_one(i,j)/sum_col(j); %计算出归一化后每个元素在所在特征列的占比
    end
end

E_ele = [];
for i = 1:row
    for j = 1:col
        if ele_weight(i,j) == 0 %规定0*ln(0) = 0,不赋值默认为0
            continue
        end
        E_ele(i,j) = -ele_weight(i,j)*log(ele_weight(i,j));%计算信息熵
    end
end

E = sum(E_ele./log(row));%计算此特征的信息熵
sum_E = sum(E);
W = (1-E)./(col-sum_E);%通过信息熵计算对应特征的权重
W = W';%转置便于矩阵乘法直接计算出对应的评价分数

data * W