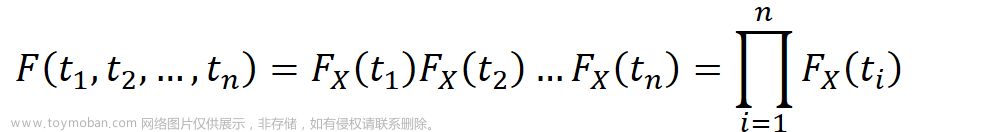样本方差的分布
根 据 中 心 极 限 定 理 可 知 样 本 均 值 X − 是 一 个 随 机 变 量 并 且 其 分 布 近 似 于 正 态 分 布 , 那 么 样 本 方 差 的 情 况 如 何 ? 对 于 独 立 同 分 布 的 X 1 , ⋯ X n ∼ N ( μ , σ 2 ) , 样 本 方 差 S n 2 = 1 n − 1 ∑ j = 1 n ( X j − X − n ) 2 也 是 随 机 变 量 , 并 且 ( n − 1 ) S n 2 σ 2 ∼ χ n − 1 2 关 于 证明 个 人 总 结 如 下 : 首先确定独立关系 对 于 独 立 同 分 布 的 X 1 , ⋯ X n ∼ N ( μ , σ 2 ) , 其 样 本 均 值 X − n 与 样 本 方 差 S n 2 相 互 独 立 , 确 切 说 是 X − n 与 X j − X − n 相 互 独 立 , 于 是 g ( X − n ) 与 h ( X j − X − n ) 相 互 独 立 , g 与 h 是 关 于 两 个 变 量 的 任 意 函 数 。 这 里 准 确 来 说 g 与 h 是 自 变 量 为 随 机 向 量 的 B o r e l 函 数 , 例 如 g ( X ) = g ( x 1 , x 2 ⋯ , x n ) , h ( Y ) = h ( y 1 , y 2 , ⋯ , y n ) , 如 果 随 机 向 量 X 与 Y 相 互 独 立 那 么 随 机 向 量 函 数 g ( X ) 与 h ( Y ) 是 相 互 独 立 的 于 是 如 果 设 h ( X j − X − n ) = n − 1 σ 2 ⋅ ∑ j = 1 n ( X j − X n − ) 2 n − 1 = ( n − 1 ) S n 2 σ 2 , g ( X − n ) = ( X − n − μ σ / n ) 2 , 那 么 ( X − n − μ σ / n ) 2 与 ( n − 1 ) S n 2 σ 2 相 互 独 立 。 其次建立关系式 ( n − 1 ) S n 2 = ∑ j = 1 n ( X j − X − n ) 2 = ∑ j = 1 n ( X j − μ + μ − X − n ) 2 = ∑ j = 1 n ( X j − μ ) 2 + ∑ j = 1 n ( X − n − μ ) 2 − 2 ( X n − − μ ) ∑ j = 1 n ( X j − μ ) = ∑ j = 1 n ( X j − μ ) 2 + n ( X − n − μ ) 2 − 2 ( X n − − μ ) n ( X − n − μ ) = ∑ j = 1 n ( X j − μ ) 2 − n ( X − n − μ ) 2 等 式 两 边 除 以 σ 2 可 得 ( n − 1 ) S n 2 σ 2 = ∑ j = 1 n ( X j − μ σ ) 2 − ( X − n − μ σ / n ) 2 ⇒ 移 位 ( n − 1 ) S n 2 σ 2 + ( X − n − μ σ / n ) 2 = ∑ j = 1 n ( X j − μ σ ) 2 转 化 一 , 由 于 E ( X − n ) = μ , V a r ( X − n ) = σ 2 n , S D ( X − n ) = σ n , 所 以 X − n − μ σ / n 其 实 是 将 X − n 标 准 化 , 而 根 据 正 态 分 布 的 和 依 然 是 正 态 分 布 的 性 质 , X − n 同 样 服 从 正 态 分 布 , 所 以 X − n − μ σ / n 是 对 一 个 正 态 分 布 的 标 准 化 , 其 结 果 自 然 为 一 个 标 准 正 态 分 布 Z ∼ N ( 0 , 1 ) , 所 以 可 得 ( X − n − μ σ / n ) 2 = Z 1 2 转 化 二 , 同 理 X j − μ σ 是 对 X j 的 标 准 化 , 而 X j 服 从 正 态 分 布 , 所 以 ∑ j = 1 n ( X j − μ σ ) 2 = ∑ j = 1 n Z j 2 Z j ∼ N ( 0 , 1 ) 通 过 上 面 两 步 转 化 等 式 ( n − 1 ) S n 2 σ 2 + ( X − n − μ σ / n ) 2 = ∑ j = 1 n ( X j − μ σ ) 2 ⇒ 可 变 为 ( n − 1 ) S n 2 σ 2 + Z 1 2 = ∑ j = 1 n Z j 2 最后使用矩母函数的性质 如 果 两 个 随 机 变 量 X 与 Y 相 互 独 立 , 那 么 X + Y 的 矩 母 函 数 是 M X + Y ( t ) = M X ( t ) M Y ( t ) , 也 就 E ( e t ( X + Y ) ) = E ( e t X ) E ( e t Y ) 由 于 ( n − 1 ) S n 2 σ 2 与 ( X − n − μ σ / n ) 2 相 互 独 立 , 所 以 对 ( n − 1 ) S n 2 σ 2 + Z 1 2 = ∑ j = 1 n Z j 2 等 式 两 边 取 其 矩 母 函 数 可 得 ( ( n − 1 ) S n 2 σ 2 的 矩 母 函 数 ) ⋅ ( 1 1 − 2 t ) 1 2 = ( 1 1 − 2 t ) n 2 ⟹ ( n − 1 ) S n 2 σ 2 的 矩 母 函 数 = ( 1 1 − 2 t ) n − 1 2 , 而 这 正 是 χ n − 1 2 的 矩 母 函 数 根 据 矩 母 函 数 的 唯 一 性 , 具 有 相 同 矩 母 函 数 的 变 量 的 分 布 相 同 , 于 是 最 终 可 得 ( n − 1 ) S n 2 σ 2 ∼ χ n − 1 2 \begin{aligned} &根据中心极限定理可知样本均值\overset{-}{X}是一个随机变量并且其分布近似于正态分布,那么样本方差的情况如何?\\ &对于独立同分布的X_1,\cdots X_n\thicksim N(\mu,\sigma^2),样本方差S_n^2=\frac{1}{n-1}\sum_{j=1}^n(X_j-\overset{-}{X}_n)^2也是随机变量,并且\\ &\frac{(n-1)S_n^2}{\sigma^2}\thicksim \chi_{n-1}^2\\\\ &关于\textcolor{blue}{\textbf{证明}}个人总结如下:\\ &\textcolor{blue}{\textbf{首先确定独立关系}}\\ &对于独立同分布的X_1,\cdots X_n\thicksim N(\mu,\sigma^2),其样本均值\overset{-}{X}_n与样本方差S_n^2相互独立,确切说是\overset{-}{X}_n与X_j-\overset{-}{X}_n\\ &相互独立,于是g(\overset{-}{X}_n)与h(X_j-\overset{-}{X}_n)相互独立,g与h是关于两个变量的任意函数。\\ &这里准确来说g与h是自变量为随机向量的Borel函数,例如g(X)=g(x_1,x_2\cdots,x_n),h(Y)=h(y_1,y_2,\cdots,y_n),\\ &如果随机向量X与Y相互独立那么随机向量函数g(X)与h(Y)是相互独立的\\ &于是如果设h(X_j-\overset{-}{X}_n)=\frac{n-1}{\sigma^2}\cdot \sum_{j=1}^n\frac{(X_j-\overset{-}{X_n})^2}{n-1}=\frac{(n-1)S_n^2}{\sigma^2},g(\overset{-}{X}_n)=(\frac{\overset{-}{X}_n-\mu}{\sigma/\sqrt{n}})^2,那么(\frac{\overset{-}{X}_n-\mu}{\sigma/\sqrt{n}})^2与\frac{(n-1)S_n^2}{\sigma^2}\\ &相互独立。\\\\ &\textcolor{blue}{\textbf{其次建立关系式}}\\ &(n-1)S_n^2=\sum_{j=1}^n(X_j-\overset{-}{X}_n)^2=\sum_{j=1}^n(X_j-\mu+\mu-\overset{-}{X}_n)^2\\ &\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{j=1}^n(X_j-\mu)^2+\sum_{j=1}^n(\overset{-}{X}_n-\mu)^2-2(\overset{-}{X_n}-\mu)\sum_{j=1}^n(X_j-\mu)\\ &\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{j=1}^n(X_j-\mu)^2+n(\overset{-}{X}_n-\mu)^2-2(\overset{-}{X_n}-\mu)n(\overset{-}{X}_n-\mu)\\ &\qquad\qquad\qquad\qquad\qquad\qquad=\sum_{j=1}^n(X_j-\mu)^2-n(\overset{-}{X}_n-\mu)^2\\ &等式两边除以\sigma^2可得\frac{(n-1)S_n^2}{\sigma^2}=\sum_{j=1}^n(\frac{X_j-\mu}{\sigma})^2-(\frac{\overset{-}{X}_n-\mu}{\sigma/\sqrt{n}})^2\xRightarrow{移位}\frac{(n-1)S_n^2}{\sigma^2}+(\frac{\overset{-}{X}_n-\mu}{\sigma/\sqrt{n}})^2=\sum_{j=1}^n(\frac{X_j-\mu}{\sigma})^2\\ &\textcolor{green}{转化一},由于E(\overset{-}{X}_n)=\mu,Var(\overset{-}{X}_n)=\frac{\sigma^2}{n},SD(\overset{-}{X}_n)=\frac{\sigma}{\sqrt{n}},所以\frac{\overset{-}{X}_n-\mu}{\sigma/\sqrt{n}}其实是将\overset{-}{X}_n标准化,而根据正态分布\\ &的和依然是正态分布的性质,\overset{-}{X}_n同样服从正态分布,所以\frac{\overset{-}{X}_n-\mu}{\sigma/\sqrt{n}}是对一个正态分布的标准化,其结果自然为一个\\&标准正态分布Z\thicksim N(0,1),所以可得(\frac{\overset{-}{X}_n-\mu}{\sigma/\sqrt{n}})^2=Z_1^2 \\ &\textcolor{green}{转化二},同理\frac{X_j-\mu}{\sigma}是对X_j的标准化,而X_j服从正态分布,所以 \sum_{j=1}^n(\frac{X_j-\mu}{\sigma})^2=\sum_{j=1}^nZ_j^2\quad Z_j\thicksim N(0,1)\\ &通过上面两步转化等式\frac{(n-1)S_n^2}{\sigma^2}+(\frac{\overset{-}{X}_n-\mu}{\sigma/\sqrt{n}})^2=\sum_{j=1}^n(\frac{X_j-\mu}{\sigma})^2\xRightarrow{可变为}\frac{(n-1)S_n^2}{\sigma^2}+Z_1^2=\sum_{j=1}^nZ_j^2\\\\ &\textcolor{blue}{\textbf{最后使用矩母函数的性质}}\\ &\color{red}如果两个随机变量X与Y相互独立,那么X+Y的矩母函数是M_{X+Y}(t)=M_X(t)M_Y(t),也就\color{red}E(e^{t(X+Y)})=E(e^{tX})E(e^{tY})\\ &由于\frac{(n-1)S_n^2}{\sigma^2}与(\frac{\overset{-}{X}_n-\mu}{\sigma/\sqrt{n}})^2相互独立,所以对\frac{(n-1)S_n^2}{\sigma^2}+Z_1^2=\sum_{j=1}^nZ_j^2等式两边取其矩母函数可得\\ &\displaystyle {\LARGE(}\frac{(n-1)S_n^2}{\sigma^2}的矩母函数{\LARGE)}\cdot(\frac{1}{1-2t})^{\frac{1}{2}}=(\frac{1}{1-2t})^{\frac{n}{2}}\implies \frac{(n-1)S_n^2}{\sigma^2}的矩母函数 = (\frac{1}{1-2t})^{\frac{n-1}{2}},而这正是\chi_{n-1}^2的矩母函数\\ &根据矩母函数的唯一性,具有相同矩母函数的变量的分布相同,于是最终可得\frac{(n-1)S_n^2}{\sigma^2}\thicksim \chi_{n-1}^2 \end{aligned} 根据中心极限定理可知样本均值X−是一个随机变量并且其分布近似于正态分布,那么样本方差的情况如何?对于独立同分布的X1,⋯Xn∼N(μ,σ2),样本方差Sn2=n−11j=1∑n(Xj−X−n)2也是随机变量,并且σ2(n−1)Sn2∼χn−12关于证明个人总结如下:首先确定独立关系对于独立同分布的X1,⋯Xn∼N(μ,σ2),其样本均值X−n与样本方差Sn2相互独立,确切说是X−n与Xj−X−n相互独立,于是g(X−n)与h(Xj−X−n)相互独立,g与h是关于两个变量的任意函数。这里准确来说g与h是自变量为随机向量的Borel函数,例如g(X)=g(x1,x2⋯,xn),h(Y)=h(y1,y2,⋯,yn),如果随机向量X与Y相互独立那么随机向量函数g(X)与h(Y)是相互独立的于是如果设h(Xj−X−n)=σ2n−1⋅j=1∑nn−1(Xj−Xn−)2=σ2(n−1)Sn2,g(X−n)=(σ/nX−n−μ)2,那么(σ/nX−n−μ)2与σ2(n−1)Sn2相互独立。其次建立关系式(n−1)Sn2=j=1∑n(Xj−X−n)2=j=1∑n(Xj−μ+μ−X−n)2=j=1∑n(Xj−μ)2+j=1∑n(X−n−μ)2−2(Xn−−μ)j=1∑n(Xj−μ)=j=1∑n(Xj−μ)2+n(X−n−μ)2−2(Xn−−μ)n(X−n−μ)=j=1∑n(Xj−μ)2−n(X−n−μ)2等式两边除以σ2可得σ2(n−1)Sn2=j=1∑n(σXj−μ)2−(σ/nX−n−μ)2移位σ2(n−1)Sn2+(σ/nX−n−μ)2=j=1∑n(σXj−μ)2转化一,由于E(X−n)=μ,Var(X−n)=nσ2,SD(X−n)=nσ,所以σ/nX−n−μ其实是将X−n标准化,而根据正态分布的和依然是正态分布的性质,X−n同样服从正态分布,所以σ/nX−n−μ是对一个正态分布的标准化,其结果自然为一个标准正态分布Z∼N(0,1),所以可得(σ/nX−n−μ)2=Z12转化二,同理σXj−μ是对Xj的标准化,而Xj服从正态分布,所以j=1∑n(σXj−μ)2=j=1∑nZj2Zj∼N(0,1)通过上面两步转化等式σ2(n−1)Sn2+(σ/nX−n−μ)2=j=1∑n(σXj−μ)2可变为σ2(n−1)Sn2+Z12=j=1∑nZj2最后使用矩母函数的性质如果两个随机变量X与Y相互独立,那么X+Y的矩母函数是MX+Y(t)=MX(t)MY(t),也就E(et(X+Y))=E(etX)E(etY)由于σ2(n−1)Sn2与(σ/nX−n−μ)2相互独立,所以对σ2(n−1)Sn2+Z12=j=1∑nZj2等式两边取其矩母函数可得(σ2(n−1)Sn2的矩母函数)⋅(1−2t1)21=(1−2t1)2n⟹σ2(n−1)Sn2的矩母函数=(1−2t1)2n−1,而这正是χn−12的矩母函数根据矩母函数的唯一性,具有相同矩母函数的变量的分布相同,于是最终可得σ2(n−1)Sn2∼χn−12文章来源地址https://www.toymoban.com/news/detail-402736.html
文章来源:https://www.toymoban.com/news/detail-402736.html
到了这里,关于样本方差分布的证明的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!