题目描述
硬币。给定数量不限的硬币,币值为25分、10分、5分和1分,编写代码计算n分有几种表示法。(结果可能会很大,你需要将结果模上1000000007)
示例1:
- 输入: n = 5
输出:2
解释: 有两种方式可以凑成总金额:
5=5
5=1+1+1+1+1
示例2:
- 输入: n = 10
输出:4
解释: 有四种方式可以凑成总金额:
10=10
10=5+5
10=5+1+1+1+1+1
10=1+1+1+1+1+1+1+1+1+1
说明:
- 你可以假设:0 <= n (总金额) <= 1000000
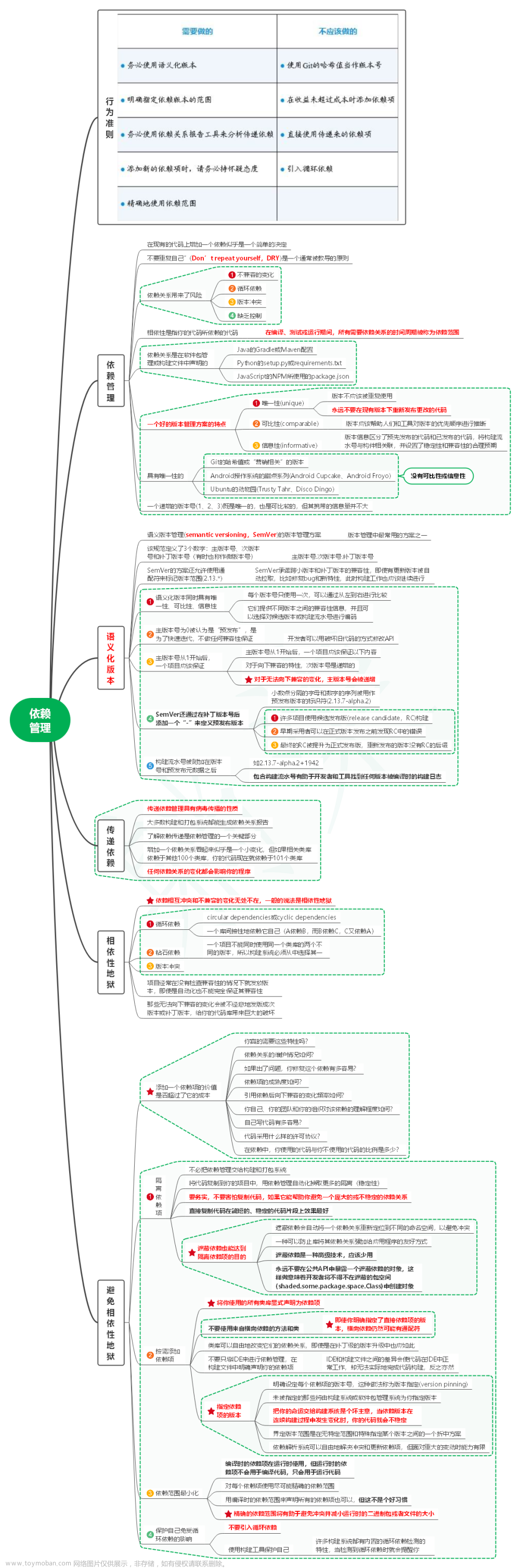
解题思路与代码
这道题我拿到手上,就有了一种拿动态规划去解决它的冲动。所以让我们来看看这道题拿动态规划怎么去解决。
方法一 :动态规划
第一步,拿到这道题,先分析dp数组的下标以及含义是什么?
- 定义一个一维数组dp,其中dp[i]表示组成金额n的钱的不同表示方法的数量。
第二步,去确定状态转移方程式什么?
- 对于每一个币值(1,5,10,25),
依次从当前硬币的价值处开始遍历直到最大金额n处停止,一共有多少种方法,那么对于当前金额j,可以得出递推公式:dp[j] = (dp[j] + dp[j - 当前币值]) % 1000000007
第三步,去初始化dp数组
- 由于下一步的结果永远都是由上一步所去推出来的,所以我们要直到第一步的数值是多少,才好去做下面的推导
- 我们要将初始化dp[0]为1,因为有一种表示方法是使用0个硬币组成0分。其余元素初始化为0。
第四步,确定如何遍历dp数组。
- 我们要用一个双层的for循环去遍历这个dp数组,这是因为,我们一共有4种硬币的面值。所以我们要一次选择每一种面值的数额去作为其实遍历的点,直到达到题目要求的n时停止。
- 那么代码大概就是这样:
for(int& coin : coins)
for(int i = coin; i < n+1; ++i)
dp[i] = (dp[i] + dp[i - coin])%MOD;
第五步,举例推导dp数组
- 这一步自己在纸上画一画就好了
具体的解决代码如下:
class Solution {
public:
int waysToChange(int n) {
int MOD = 1000000007;
vector<int> dp(n+1);
vector<int> coins{1,5,10,25};
dp[0] = 1;
for(int& coin : coins)
for(int i = coin; i < n+1; ++i)
dp[i] = (dp[i] + dp[i - coin])%MOD;
return dp[n];
}
};
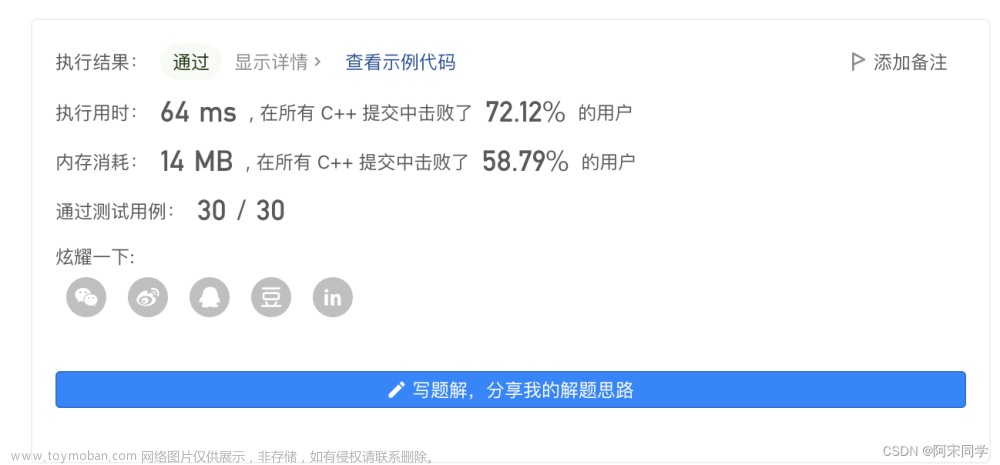
复杂度分析
时间复杂度:O(n),其中n为输入金额。这是因为代码中有两层循环,第一层循环遍历硬币,它是一个常数4(币值:1, 5, 10, 25),第二层循环遍历所有金额,从硬币面值到n。因此,总时间复杂度是O(4n),可以简化为O(n)。
空间复杂度:O(n),其中n为输入金额。代码中主要的空间消耗来自dp数组,它的大小为n + 1。因此,空间复杂度为O(n)。
总结
这道题是动态规划里的一道组合类问题。我尝试着把这道题往0-1背包去靠,结果有点费劲。不如就像我这么去解释。
不要硬生生的划分给0-1背包,这就是一道动态规划的组合问题而已。文章来源:https://www.toymoban.com/news/detail-402969.html
难度确实始终,也很好理解。但你要往0-1背包去靠,那就很难理解了。我个人感觉。文章来源地址https://www.toymoban.com/news/detail-402969.html
到了这里,关于《程序员面试金典(第6版)》 面试题 08.11. 硬币(动态规划,组合问题,C++)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!