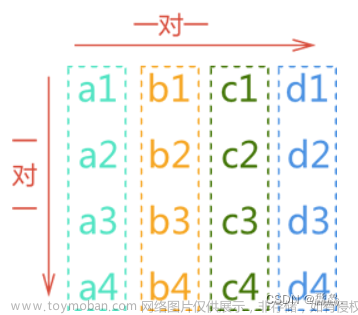
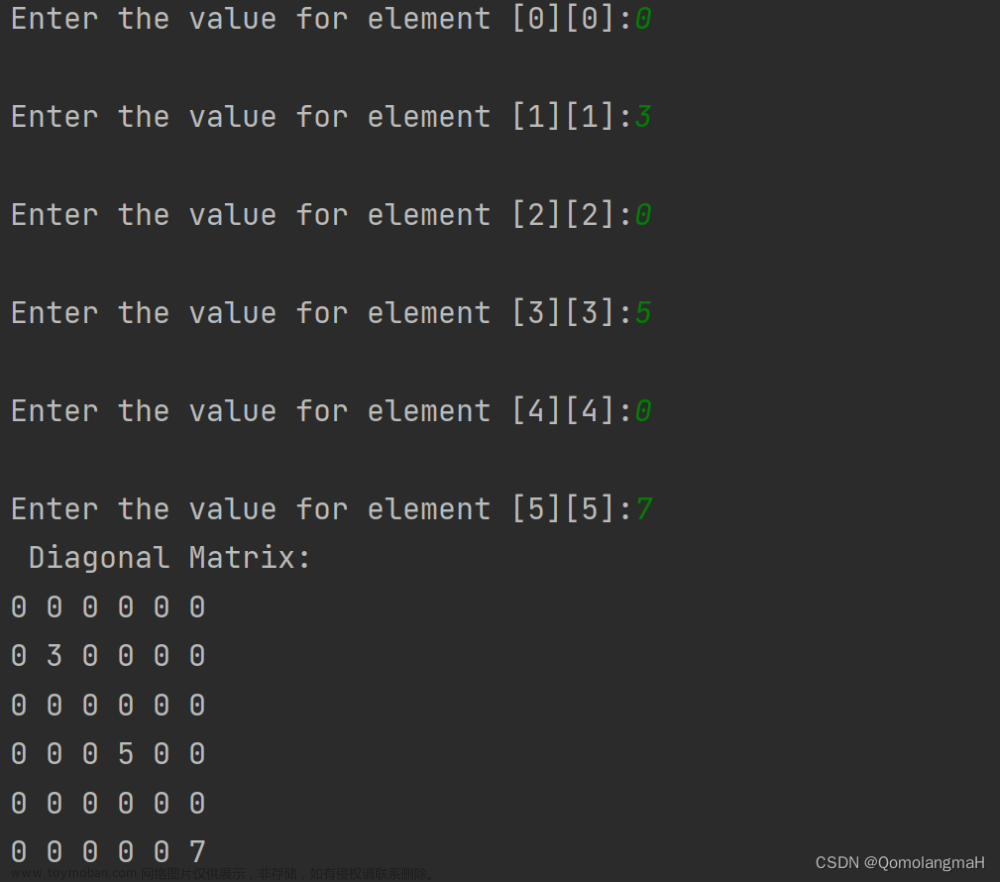
1. 对称矩阵
对称矩阵的定义：
若n阶方阵中任意一个元素a,都有a(i,j)=a(j,i)则该矩阵为对称矩阵
也就是说对称矩阵的元素关于对角线对称。对角线上半部分称为上三角区，下半部分称为下三角区。
对称矩阵的压缩存储策略：只存储主对角线+下三角区(或主对角线+上三角区)
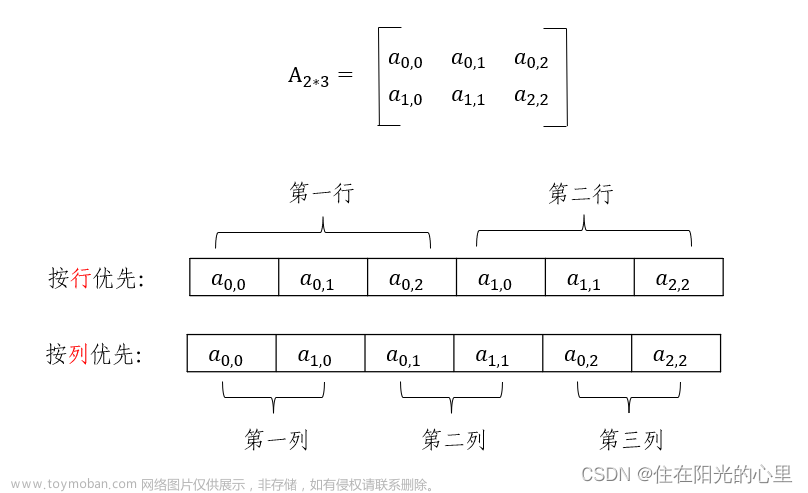
可以定义一维数组，将这些元素按照行优先的方式存储。
这个一维数组的大小（1+2+3+……+n）=(1+n)*n/2
矩阵还原过程（原矩阵的行号，列号映射到一维数组的下标）
按照行优先策略先计算 a(i,j)是矩阵的第几个元素
[1+2+3+……+i-1]+j个元素=（i-1）*i/2个元素
说明这个元素在一维数组的下标为[（i-1）*i/2]-1 数组下标从0开始
如果访问的是没有保存到一维数组的那半部分数据，可以根据对称原理找到对称位置的元素即可。
2. 三角矩阵
下三角矩阵：
下三角矩阵：除了主对角线和下三角区，其余的元素都相同
上三角矩阵与之类似。
压缩存储策略：按行优先原则将橙色区元素存入一维数组中。并在最后一个位置存储常量c
矩阵还原过程（原矩阵的行号，列号映射到一维数组的下标） 这里使用下三角矩阵为例
[1+2+3+……+i-1]+j个元素=j+（i-1）*i/2个元素
说明这个元素在一维数组的下标为[j+（i-1）*i/2]-1 数组下标从0开始
如果访问的是上半个三角元素，直接将其映射到一维数组的最后一个位置[(n+1)*n/2]
3. 三对角矩阵
三对角矩阵，又称带状矩阵：当|i-j>1时，有aj= 0 (1<i, j ≤n)
压缩存储策略：按行优先(或列优先）原则，只存储带状部分
带状矩阵第一行和最后一行是2个元素，中间行元素都是三个。
n阶带状矩阵 数组大小为3n-2
矩阵还原过程（原矩阵的行号，列号映射到一维数组的下标）
-
|i-j|>1 值为0，不需要到一维数组哪里查找。
-
|i-j|≤1 找a(i,j)是数组第几个元素即可
3(i-1)-1+j-i+2=2*i+j-2对应数组下标2i+j-3
4. 稀疏矩阵
稀疏矩阵：非零元素远远少矩阵元素的个数
压缩存储策略：
-
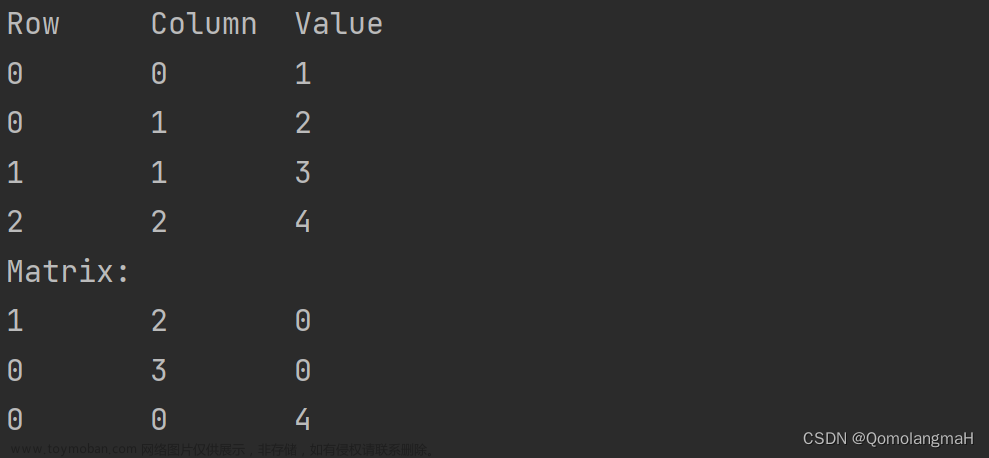
顺序存储：使用三元组形式存储<行，列，值>
-
十字链表法：一条链表代表稀疏矩阵的行，另一条链表代表稀疏矩阵的列。
非零元素节点声明：值+行号+列号+同行的下一个节点指针+同列的下一个节点指针。文章来源：https://www.toymoban.com/news/detail-402971.html
文章来源地址https://www.toymoban.com/news/detail-402971.html
到了这里，关于数据结构-拓展突破-特殊矩阵（对称矩阵，三角矩阵，三对角矩阵，稀疏矩阵）的压缩存储）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
