【leetcode刷题】66.使用最小花费爬楼梯—

这篇具有很好参考价值的文章主要介绍了【leetcode刷题】66.使用最小花费爬楼梯——Java版。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

⭐欢迎订阅《leetcode》专栏，每日一题，每天进步⭐

我觉得这个题的描述应该改改：每个阶梯都有一定数量坨屎，一次只能跨一个或者两个阶梯，走到一个阶梯就要吃光上面的屎，问怎么走才能吃最少的屎？开局你选前两个阶梯的其中一个作为开头点，并吃光该阶梯的屎。

——leetcode此题热评

前言

哈喽，大家好，我是一条。

糊涂算法，难得糊涂

点击跳转到《糊涂算法》专栏学习java大厂面试必备数据结构和算法知识！

Question

746. 使用最小花费爬楼梯

难度：简单

数组的每个下标作为一个阶梯，第 i 个阶梯对应着一个非负数的体力花费值 cost[i]（下标从 0 开始）。

每当你爬上一个阶梯你都要花费对应的体力值，一旦支付了相应的体力值，你就可以选择向上爬一个阶梯或者爬两个阶梯。

请你找出达到楼层顶部的最低花费。在开始时，你可以选择从下标为 0 或 1 的元素作为初始阶梯。

示例 1：

输入：cost = [10, 15, 20]
输出：15
解释：最低花费是从 cost[1] 开始，然后走两步即可到阶梯顶，一共花费 15 。
示例 2：

输入：cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
输出：6
解释：最低花费方式是从 cost[0] 开始，逐个经过那些 1 ，跳过 cost[3] ，一共花费 6 。

提示：

cost 的长度范围是 [2, 1000]。
cost[i] 将会是一个整型数据，范围为 [0, 999] 。

Solution

先回顾一下《爬楼梯》这个题

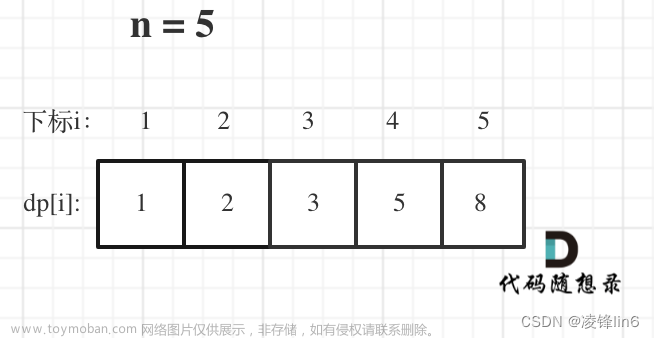
假如要到达某一层，只要考虑两件事：是从楼下走1层上来，还是从楼下的楼下跨2层上来。所以就有了 dp[i] = min(dp[i-1]+down, dp[i-2]+downdown)

Code

所有leetcode代码已同步至github

欢迎star

/**
 * @author 一条coding
 */
class Solution {
 public int minCostClimbingStairs(int[] cost) {
        int n=cost.length;
        int down=0;  int downdown=0;
        for(int i=2;i<=n;i++){
            int cur = Math.min(cost[i-1]+down,cost[i-2]+downdown);   // 到当前楼层两种路径消耗的体力最小值
            downdown=down;       //及时更新便于下一层循环，楼下就变成了楼下的楼下
            down=cur;      //当前楼层就变成了楼下
        }
        return down;  //本该返回cur，不过cur是局部变量，但到达当前楼层的体力值cur在循环里已经赋值给了down
    }
}