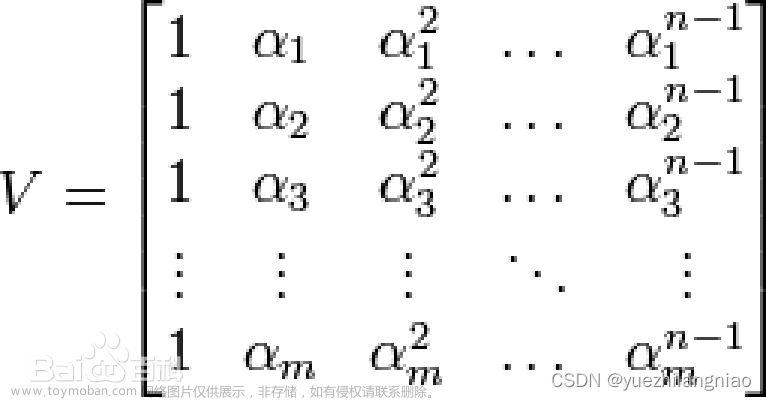
前置知识:
- 行列式的性质
- 逆矩阵的性质
- 【定义】矩阵的秩
- 线性方程组与矩阵的秩
- 矩阵初等变换与矩阵乘法的联系
前置定义 2 设在矩阵 A \boldsymbol{A} A 中有一个不等于 0 0 0 的 r r r 阶子式 D D D,且所有 r + 1 r+1 r+1 阶子式(如果存在的话)全等于 0 0 0,那么 D D D 称为矩阵 A \boldsymbol{A} A 的 最高阶非零子式,数 r r r 称为 矩阵 A \boldsymbol{A} A 的秩,记作 R ( A ) R(\boldsymbol{A}) R(A)。并规定零矩阵的秩等于 0 0 0。
说明见 “【定义】矩阵的秩”。
前置性质 3 行列式与它的转置行列式相等。
证明见 “行列式的性质”。
前置定理 4 若矩阵 A \boldsymbol{A} A 可逆,则 ∣ A ∣ ≠ 0 |\boldsymbol{A}| \ne 0 ∣A∣=0。
证明见 “逆矩阵的性质”。
前置定理 5 设 A ∼ r B \boldsymbol{A} \stackrel{r}{\sim} \boldsymbol{B} A∼rB,则 A \boldsymbol{A} A 与 B \boldsymbol{B} B 中非零子式的最高阶数相等。
证明见 “【定义】矩阵的秩”。
前置定理 6 设 A \boldsymbol{A} A 和 B \boldsymbol{B} B 为 $m \times n $ 矩阵,那么 A ∼ B \boldsymbol{A} \sim \boldsymbol{B} A∼B 的充分必要条件是存在 m m m 阶可逆矩阵 P \boldsymbol{P} P 和 n n n 阶可逆矩阵 Q \boldsymbol{Q} Q,使 P A Q = B \boldsymbol{P} \boldsymbol{A} \boldsymbol{Q} = \boldsymbol{B} PAQ=B。
证明见 “矩阵初等变换与矩阵乘法的联系“。
1 矩阵的秩与矩阵是否可逆的关系
定理 1 逆矩阵的秩等于矩阵的阶数,不可逆矩阵的秩小于矩阵的阶数。
证明 对于 n n n 阶矩阵 A \boldsymbol{A} A,由于 A \boldsymbol{A} A 的 n n n 阶子式只有一个 ∣ A ∣ |\boldsymbol{A}| ∣A∣,故当 ∣ A ∣ ≠ 0 |\boldsymbol{A}| \ne 0 ∣A∣=0 时 R ( A ) = n R(\boldsymbol{A}) = n R(A)=n,当 ∣ A ∣ = 0 |\boldsymbol{A}| = 0 ∣A∣=0 时 R ( A ) < n R(\boldsymbol{A}) < n R(A)<n。根据前置定理 4,得证。
因此,可逆矩阵又称为 满秩矩阵,不可逆矩阵(奇异矩阵)又称 降秩矩阵。
2 矩阵的秩与矩阵行数、列数的关系
性质 1 若 A \boldsymbol{A} A 为 m × n m \times n m×n 矩阵,则 0 ≤ R ( A ) ≤ min { m , n } 0 \le R(\boldsymbol{A}) \le \min \{m,n\} 0≤R(A)≤min{m,n}。
证明 根据前置定义 2,显然成立。
性质 2 R ( A T ) = R ( A ) R(\boldsymbol{A}^T) = R(\boldsymbol{A}) R(AT)=R(A)。
证明 根据前置性质 3,行列式与其转置行列式相等,因此 A T \boldsymbol{A}^T AT 的子式与 A \boldsymbol{A} A 的子式对应相等,从而 R ( A T ) = R ( A ) R(\boldsymbol{A}^T) = R(\boldsymbol{A}) R(AT)=R(A)。
3 矩阵的秩与矩阵初等变换的关系
性质 3 若 A ∼ B \boldsymbol{A} \sim \boldsymbol{B} A∼B,则 R ( A ) = R ( B ) R(\boldsymbol{A}) = R(\boldsymbol{B}) R(A)=R(B)。
证明 根据前置定理 5 可知,矩阵 A \boldsymbol{A} A 经初等行变换变成矩阵 B \boldsymbol{B} B 时,矩阵的秩不变。因此,我们只需要证明矩阵 A \boldsymbol{A} A 经初等列变换变成矩阵 B \boldsymbol{B} B 时,矩阵的秩也不变即可。
根据前置定理 5,矩阵 A T \boldsymbol{A}^T AT 经初等行变换变成矩阵 B T \boldsymbol{B}^T BT 时,矩阵的秩不变,即 R ( A T ) = R ( B T ) R(\boldsymbol{A}^T) = R(\boldsymbol{B}^T) R(AT)=R(BT)。根据性质 2 可知, R ( A ) = R ( A T ) R(\boldsymbol{A}) = R(\boldsymbol{A}^T) R(A)=R(AT), R ( B ) = R ( B T ) R(\boldsymbol{B}) = R(\boldsymbol{B}^T) R(B)=R(BT),于是有 R ( A ) = R ( B ) R(\boldsymbol{A}) = R(\boldsymbol{B}) R(A)=R(B)。
综上所述,若矩阵 A \boldsymbol{A} A 经有限次初等变换变为矩阵 B \boldsymbol{B} B(即 A ∼ B \boldsymbol{A} \sim \boldsymbol{B} A∼B),则 R ( A ) = R ( B ) R(\boldsymbol{A}) = R(\boldsymbol{B}) R(A)=R(B)。
根据性质 3,我们发现:矩阵的初等变换作为一种运算,其深刻意义在于它不改变矩阵的秩。
根据前置定理 6 替换性质 3 中的条件,得到性质如下:
性质 4 若可逆矩阵 P \boldsymbol{P} P、 Q \boldsymbol{Q} Q 使 P A Q = B \boldsymbol{P} \boldsymbol{A} \boldsymbol{Q} = \boldsymbol{B} PAQ=B,则 R ( A ) = R ( B ) R(\boldsymbol{A}) = R(\boldsymbol{B}) R(A)=R(B)。
证明:根据前置定理 6 和性质 3,显然成立。
4 矩阵的秩和矩阵分块的关系
性质 5 max { R ( A ) , R ( B ) } ≤ R ( A , B ) ≤ R ( A ) + R ( B ) \max \{R(\boldsymbol{A}), R(\boldsymbol{B})\} \le R(\boldsymbol{A},\boldsymbol{B}) \le R(\boldsymbol{A}) + R(\boldsymbol{B}) max{R(A),R(B)}≤R(A,B)≤R(A)+R(B)。
证明 因为 A \boldsymbol{A} A 的最高阶非零子式总是 ( A , B ) (\boldsymbol{A},\boldsymbol{B}) (A,B) 的非零子式,所以 R ( A ) ≤ R ( A , B ) R(\boldsymbol{A}) \le R(\boldsymbol{A},\boldsymbol{B}) R(A)≤R(A,B)。同理有 R ( B ) ≤ R ( A , B ) R(\boldsymbol{B}) \le R(\boldsymbol{A},\boldsymbol{B}) R(B)≤R(A,B)。根据以上两式可得
max { R ( A ) , R ( B ) } ≤ R ( A , B ) \max \{R(\boldsymbol{A}), R(\boldsymbol{B})\} \le R(\boldsymbol{A},\boldsymbol{B}) max{R(A),R(B)}≤R(A,B)
设 R ( A ) = r R(\boldsymbol{A}) = r R(A)=r, R ( B ) = t R(\boldsymbol{B}) = t R(B)=t;把 A T \boldsymbol{A}^T AT 和 B T \boldsymbol{B}^T BT 分别作初等行变换化为行阶梯形矩阵 A ~ \tilde{\boldsymbol{A}} A~ 和 B ~ \tilde{\boldsymbol{B}} B~。因为根据性质 2 有 R ( A T ) = R ( A ) = r R(\boldsymbol{A}^T) = R(\boldsymbol{A}) = r R(AT)=R(A)=r, R ( B T ) = R ( B ) = t R(\boldsymbol{B}^T) = R(\boldsymbol{B}) = t R(BT)=R(B)=t,所以 A ~ \tilde{\boldsymbol{A}} A~ 和 B ~ \tilde{\boldsymbol{B}} B~ 中分别包含 r r r 和非零行和 t t t 的非零行,从而 ( A ~ B ~ ) \begin{pmatrix} \tilde{\boldsymbol{A}} \\ \tilde{\boldsymbol{B}} \end{pmatrix} (A~B~) 中只含有 r + t r+t r+t 个非零行,并且 ( A T B T ) ∼ r ( A ~ B ~ ) \begin{pmatrix} \boldsymbol{A}^T \\ \boldsymbol{B}^T \end{pmatrix} \stackrel{r}{\sim} \begin{pmatrix} \tilde{\boldsymbol{A}} \\ \tilde{\boldsymbol{B}} \end{pmatrix} (ATBT)∼r(A~B~)。于是有
R ( A , B ) = R ( A T B T ) T = R ( A T B T ) = R ( A ~ B ~ ) ≤ r + t = R ( A ) = R ( B ) R(\boldsymbol{A},\boldsymbol{B}) = R\begin{pmatrix} \boldsymbol{A}^T \\ \boldsymbol{B}^T \end{pmatrix}^T = R \begin{pmatrix} \boldsymbol{A}^T \\ \boldsymbol{B}^T \end{pmatrix} = R \begin{pmatrix} \tilde{\boldsymbol{A}} \\ \tilde{\boldsymbol{B}} \end{pmatrix} \le r + t = R(\boldsymbol{A}) = R(\boldsymbol{B}) R(A,B)=R(ATBT)T=R(ATBT)=R(A~B~)≤r+t=R(A)=R(B)
得证。
特别地,当
B
=
b
\boldsymbol{B} = \boldsymbol{b}
B=b 为非零列向量时,有
R
(
A
)
≤
R
(
A
,
b
)
≤
R
(
A
)
+
1
R(\boldsymbol{A}) \le R(\boldsymbol{A},\boldsymbol{b}) \le R(\boldsymbol{A}) + 1
R(A)≤R(A,b)≤R(A)+1
性质 6 R ( A + B ) ≤ R ( A ) + R ( B ) R(\boldsymbol{A} + \boldsymbol{B}) \le R(\boldsymbol{A}) + R(\boldsymbol{B}) R(A+B)≤R(A)+R(B)。
证明 不妨设 A \boldsymbol{A} A 和 B \boldsymbol{B} B 为 m × n m \times n m×n 矩阵。对矩阵 ( A + B B ) \begin{pmatrix} \boldsymbol{A}+\boldsymbol{B} \\ \boldsymbol{B} \end{pmatrix} (A+BB) 做初等行变换 r i − r n + i r_i - r_{n+i} ri−rn+i( i = 1 , 2 , ⋯ , n i = 1,2,\cdots,n i=1,2,⋯,n)即得
( A + B B ) ∼ r ( A B ) \begin{pmatrix} \boldsymbol{A}+\boldsymbol{B} \\ \boldsymbol{B} \end{pmatrix} \stackrel{r}{\sim} \begin{pmatrix} \boldsymbol{A} \\ \boldsymbol{B} \end{pmatrix} (A+BB)∼r(AB)
根据性质 5,有
R ( A + B ) ≤ R ( A + B B ) = R ( A B ) = R ( A T , B T ) T = R ( A T , B T ) ≤ R ( A T ) + R ( B T ) = R ( A ) + R ( B ) R(\boldsymbol{A} + \boldsymbol{B}) \le R \begin{pmatrix} \boldsymbol{A}+\boldsymbol{B} \\ \boldsymbol{B} \end{pmatrix} = R \begin{pmatrix} \boldsymbol{A} \\ \boldsymbol{B} \end{pmatrix} = R(\boldsymbol{A}^T,\boldsymbol{B}^T)^T = R(\boldsymbol{A}^T,\boldsymbol{B}^T) \le R(\boldsymbol{A}^T) + R(\boldsymbol{B}^T) = R(\boldsymbol{A}) + R(\boldsymbol{B}) R(A+B)≤R(A+BB)=R(AB)=R(AT,BT)T=R(AT,BT)≤R(AT)+R(BT)=R(A)+R(B)
得证。文章来源:https://www.toymoban.com/news/detail-403345.html
如果矩阵 A \boldsymbol{A} A 的秩等于它的列数,这样的矩阵称为 列满秩矩阵;当 A \boldsymbol{A} A 为方阵时,列满秩矩阵就成为满秩矩阵。如果矩阵 A \boldsymbol{A} A 的秩等于它的行数,这样的矩阵称为 行满秩矩阵;当 A \boldsymbol{A} A 为方阵时,行满秩矩阵就成为满秩矩阵。文章来源地址https://www.toymoban.com/news/detail-403345.html
到了这里,关于矩阵的秩的性质的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!