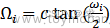一、前言
1. 设计流程

2.系统频率响应
2.1频响图
系统函数 H 是一个复数,其图谱分为:幅度谱、相位谱
- 幅度谱
x轴:模拟频率f(数字频率w转化来)【单位:赫兹Hz】
y轴:|H1|幅度【一般用:20 * log10|H1|】【单位:分贝dB】
- 相位谱
x轴:模拟频率f(数字频率w转化来)【单位:赫兹Hz】
y轴:H1 的相位
2.2 各个频率转换关系

- 【为采样率】
- 所以可以推出f:
3.巴特沃斯滤波器简介
N:滤波器阶数
:3dB截止频率

3.1特点
- 最大平坦性
在截止频率前较为平坦,这个平坦也保证了信号的原始值,不会因为滤波被衰减。巴特沃斯低通滤波器的通频带最大扁平效应使通频带的增益得到扁平优化。(由上图可知:N值越大,通频带越平坦)
- 幅频特性、相频特性都是单调递减
巴特沃斯低通滤波器是全极点滤波器,所有零点都在无穷远处;它的幅度随频率的增加而单调下降,且频率无穷大时它的幅度才衰减完。
3.2设计思路
- 幅度平方函数:表现了N 阶巴特沃斯低通滤波器的振幅和频率关系

- 传递函数
4.时域、频域、z域下的系统描述

| 时域 | z域 | 频域 | |
| 数字滤波器 特性描述方式 |
单位冲激响应 h(n) |
系统函数 H(z) |
频率响应 |
| 输出输入关系 | y(n)=x(n)*h(n) | Y(z)=X(z)·H(z) |
二、具体设计步骤
1.数字滤波器技术指标
先要已知以下指标:
- :数字通带截止频率
- :数字阻带截止频率
- :通带最大衰减(单位:dB)
- :阻带最小衰减 (单位:dB)

衰减、的推导:
2.模拟滤波器指标
【需要将数字指标转化为模拟指标:冲激响应不变法、双线性变换法的转换公式不同】
- :模拟通带截止频率
- :模拟阻带截止频率
- :通带最大衰减(单位:dB)
- :阻带最小衰减 (单位:dB)
2.1冲激响应不变法
、不变
2.2双线性变换法
【需要预畸变】
(c为任意常数,其中低通滤波器c取 )
、不变
3.过渡模拟滤波器
需要计算:
N:阶数
:3dB截止频率
3.1求阶数N
(1)计算
(2)计算归一化频率
(3)得到阶数N
(向上取整)
3.2 查表确定归一化低通原型系统函数
 3.3求3dB截止频率
3.3求3dB截止频率
【冲激响应不变法、双线性变换法公式不同】
- 冲激响应不变法:应用通带指标
(原因:冲激响应不变法需要阻带效果好)
- 双线性变换法: 应用阻带指标
3.4去归一化得到模拟系统函数
4.数字化:得到数字滤波器系统函数H(z)
4.1冲激响应不变法
先将模拟系统函数 展开成部分分式形式:
再变换成巴特沃斯数字滤波器:
4.2双线性变换法
三、Matlab代码实现
任务要求:
1.冲激响应不变法法
butttord函数
- 功能: 查找巴特沃思模拟滤波器的最小阶数n和截止频率Wc
- 格式:
[N,wc] = buttord(wp,ws,ap,as,’s’) - 参数:
wp:通带截止频率 ws :阻带截止频率
ap:通带最大允许衰减 as:阻带最小允许衰减
‘s’:表示模拟滤波器(省略s表示数字滤波器)
N: 滤波器阶数 wc: 3db截止频率
buttap 函数
- 功能:可设计出N阶巴特沃斯低通滤波器的零、极点
- 格式:
[z,p,k] = buttap(N) - 参数:
z:N阶巴特沃斯低通滤波器的零点
p:N阶巴特沃斯低通滤波器的极点
k:增益
N:阶数
zp2tf 函数
- 功能:由零极点和增益确定归一化Han(s)系数
- 格式:
[Bap,Aap]=zp2tf(z,p,k)) - 参数:
z:N阶巴特沃斯低通滤波器的零点
p:N阶巴特沃斯低通滤波器的极点
Bap:归一化系统函数Han(s)分子
Aap:归一化系统函数Han(s)分母
lp2lp 函数(低通使用)
- 功能:用s/wc 代替s,去归一化Han(s),得到H(s)
- 格式:
[Bbs,Abs]=lp2lp(Bap,Aap,wac) - 参数:
Bap:归一化系统函数Han(s)分子
Aap:归一化系统函数Han(s)分母
wac:3dB截止频率
Bbs:数字域系统函数分子
Abs:数字域系统函数分母
impinvar函数(冲激响应不变法)
- 功能:使用冲击响应不变法进行数字化
- 格式:
[b,a]=impinvar(B,A,fs) - 参数:
B,A:模拟滤波器系统函数分子分母多项式系数向量
b,a:数字滤波器系统函数分子分母多项式系数向量
fs:采样频率文章来源:https://www.toymoban.com/news/detail-403426.html
freqz函数
-
功能:求频率响应函数
-
格式:
[h,w] = freqz(b,a,n,'whole') - 参数:
输入:
b,a:数字滤波器系统函数分子分母多项式系数向量
n:计算点数(默认为512)
'whole':w范围为0-2π
输出:(若默认n,h和w大小都是512)
h:频率响应向量,为幅度【一般单位:dB,用公式20 * log10(abs(h))来转换】
w:数字角频率【画图时要转换为模拟频率f】
代码总览
clear;close all;clc
%1.数字滤波器的技术指标
ap = 1;%通带最大衰减
as = 30;%阻带最小衰减
fp = 200;%通带截止频率
fs = 400;%阻带截止频率
Fs = 1000;%抽样间隔
T = 1/Fs;
%2.将数字指标转化成模拟滤波器技术指标(采用冲激响应不变法)
wap = 2*pi*fp;
was = 2*pi*fs;
%3.设计滤波器
[N,wac] = buttord(wap,was,ap,as,'s');%计算阶数N和3dB截止频率wac
[z,p,k] = buttap(N);%创建巴特沃斯低通滤波器 z零点p极点k增益
[Bap,Aap] = zp2tf(z,p,k);%由零极点和增益确定归一化Han(s)系数
[Bbs,Abs] = lp2lp(Bap,Aap,wac);%将s/wc 代替s,去归一化
[B,A] = impinvar(Bbs,Abs,Fs);%模拟域到数字域——冲激响应不变法
[H1,w] = freqz(B,A);%根据H(z)求频率响应
%绘制数字滤波器频响幅度谱
figure(1);
f = w*Fs/(2*pi);
subplot(2,1,1);
plot(f,20*log10(abs(H1)));%绘制幅度响应
title('冲激响应不变法——巴特沃斯BLPF(幅度)');
xlabel('频率/Hz');
ylabel('H1幅值/dB');
subplot(2,1,2);
plot(f,unwrap(angle(H1)));% 绘制相位响应
xlabel('频率/Hz');
ylabel('角度/Rad');
title('冲激响应不变法——巴特沃斯BLPF(相位)'); 结果展示

2.双线性变换法
【除了数字化用到的函数不同,其它都相同】
bilinear函数
- 功能:使用双线性变换法进行数字化
- 格式:
[b,a]=bilinear(B,A,fs) - 参数:
B,A:模拟滤波器系统函数分子分母多项式系数向量
b,a:数字滤波器系统函数分子分母多项式系数向量
fs:采样频率
代码总览
clear,clc,close;
%1.数字滤波器的技术指标要求
ap = 1;%通带最大衰减
as = 30;%阻带最小衰减
fp = 200;%通带截止频率
fs = 400;%阻带截止频率
Fs = 1000;%抽样间隔
T = 1/Fs;
%2.将数字指标转化成模拟滤波器指标
wp=(2*pi*fp)/Fs;
ws=(2*pi*fs)/Fs;
% 数字指标转模拟指标 预畸变,前面要× (2/T)
wap=2*Fs*tan(wp/2);
was=2*Fs*tan(ws/2);
%3.设计模拟滤波器
[N,wac]=buttord(wap,was,ap,as,'s');% N为阶数,wac为3dB截止频率
[z,p,k]=buttap(N);% 创建巴特沃斯低通滤波器 z零点p极点k增益
[Bap,Aap]=zp2tf(z,p,k);% 由零极点和增益确定归一化Han(s)系数
[Bbs,Abs]=lp2lp(Bap,Aap,wac);% 低通到低通 计算去归一化Ha(s)
[B,A] = bilinear(Bbs,Abs,Fs); % 模拟域到数字域:双线性不变法
[H1,w] = freqz(B,A);% 根据H(z)求频率响应特性
%绘制数字滤波器频响幅度谱
figure(2);
f=w*Fs/(2*pi);
subplot(211);
plot(f,20*log10(abs(H1))); % 绘制幅度响应
title('双线性变换法——巴特沃斯BLPF(幅度)');
xlabel('频率/Hz');
ylabel('H1幅值/dB');
subplot(212);
plot(f,unwrap(angle(H1)));% 绘制相位响应
xlabel('频率/Hz');
ylabel('角度/Rad')
title('双线性变换法——巴特沃斯BLPF(相位)');结果展示
 文章来源地址https://www.toymoban.com/news/detail-403426.html
文章来源地址https://www.toymoban.com/news/detail-403426.html
到了这里,关于数字信号处理|Matlab设计巴特沃斯低通滤波器(冲激响应不变法和双线性变换法)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!