爬楼梯和爬楼梯进阶c++-Toy模板网

这篇具有很好参考价值的文章主要介绍了爬楼梯和爬楼梯进阶c++。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

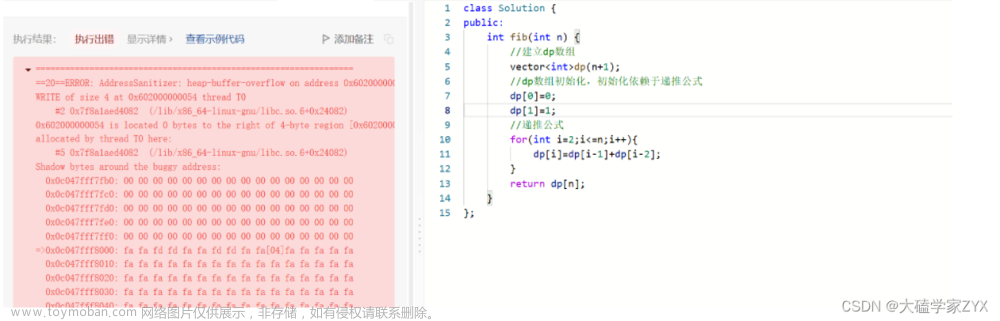
该题是动态规划入门题，可扩展性较强。主要思想参考代码随想录

题目分析

题目描述

基础爬楼梯，每次以1或2步爬楼梯，共n阶，求共有多少种爬楼梯方式
基础爬楼梯空间优化
每次爬楼梯有成本限制，如何以最小成本爬楼梯
每次爬楼梯可用步数与台阶阶数一致，如1阶可1步，2阶可1步或2步，…， n阶可1到n步前进，求爬楼梯方法数

题目分析

基础爬楼梯

每次可用1步或两步进行爬楼梯，那么每次爬楼梯的方法可往前退一步或退两步，当知道前一步或前两步的方法数时，此时的方法数就可由前一步和前两步的方法数来确定。

(1) dp数组：dp[i]，代表爬i阶的方法数总数，

(2) 递推公式：dp[i] = dp[i - 1] + dp[i - 2]；

(3) dp数组初始化：由递推公式可知，最少要初始化前两个dp数组的值，这里dp[0]的初始化存在争议，理论为0，但是为了计算dp数组，需要将其置为1，然后从i = 2开始遍历;这里可从i= 3开始遍历，越过dp[0]的初始化，dp[1] = 1; dp[2] = 2;(1 阶 + 1 阶, 2 阶),即根据遍历开始顺序初始化dp数组。

(4) 遍历顺序：由递推公式可知，要从前往后依次遍历。

(5) 打印dp数组，验证是否正确，c++中三种循环遍历方式
基础爬楼梯空间优化
这里dp数组每次只使用前两个值，可建立一个大小为2的dp数组，然后每次循环的时候更新前两个数组的值即可，此时空间复杂度为常数：O(1)；
带成本爬楼梯
数组的每个下标作为一个阶梯，第 i 个阶梯对应着一个非负数的体力花费值 cost[i]（下标从 0 开始）。每当你爬上一个阶梯你都要花费对应的体力值，一旦支付了相应的体力值，你就可以选择向上爬一个或两个。

(1) dp数组：dp[i],代表爬i阶花费的最小体力值，

(2) 递推公式：由基础爬楼梯可知，爬楼梯的方法由前两个台阶方法确定，同理，最小花费也有前两个的花费确定，但是最后要加上本级台阶的花费，故dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];

(3) 初始化方式：这里最好从0开始，因为cost是从0开始，否则需要仔细思考两者的对应关系，

(4) 同上
(5) 同上

这里也可以对空间进行优化，优化方式如上

爬楼梯阶数递增
此时每次i阶楼梯，可用1 2 3……i步去爬。则此时i阶的方法数，取决于前1-i阶的方法数，此时题目的类型也可以理解为一个完全背包问题，每阶台阶理解成一个完全背包问题，拿1-i范围内的数将这个背包填满，其中1-i个数每次可以无限取，问有多少种爬楼梯方式，便是问有多少种将背包填满的方式，关于背包问题，后序会有专门介绍，这里不过多展开

(1) dp数组：dp[i] 代表爬i阶台阶的方法数

(2) 递推公式：此时i阶的方法数，取决于前1-i阶的方法数，则dp[i] += dp[i - j], j = 1 2…i

(3) 初始化方法：同上
(4) 遍历顺序：同上
(5)验证：同上

实践步骤

动态规划解题步骤：

确定dp数组的含义
确定递推公式
dp数组初始化
确定遍历顺序
举例验证dp数组

代码实现

#include <iostream>
#include <vector>
using namespace std;

//基础爬楼梯
int climbStairs(const int& n) {
    //递归方式
    vector<int>dp(n + 1, 0);    //dp数组，代表当前台阶爬楼梯方法数
    dp[0] = 1;
    dp[1] = 1;  //另一种初始化方法，即初始化dp[1]和dp[2],从3开始遍历
    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    
    return dp[n];
}

//基础爬楼梯空间优化
int climbStairsplus(const int& n) {
    int res = 0;
    //递归方式
    vector<int>dp(2, 0);    //dp数组，代表当前台阶爬楼梯方法数
    dp[0] = 1;    //before2
    dp[1] = 1;  //before1//每次记录该该台阶的前两阶即可，但需实时更新前两节台阶数
    for (int i = 2; i <= n; i++) {
        res = dp[0] + dp[1];
        dp[0] = dp[1];
        dp[1] = res;
        
    }

    return res;
}

//带体力成本爬楼梯
int minCostClimbingStairs(vector<int>& cost) {
    vector<int> dp(cost.size());
    dp[0] = cost[0];
    dp[1] = cost[1];
    for (int i = 2; i < cost.size(); i++) {
        dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
    }
    // 注意最后一步可以理解为不用花费，所以取倒数第一步，第二步的最少值
    return min(dp[cost.size() - 1], dp[cost.size() - 2]);
}

//带体力空间优化
int minCostClimbingStairsplus(vector<int>& cost) {
    int dp0 = cost[0];
    int dp1 = cost[1];
    for (int i = 2; i < cost.size(); i++) {
        int dpi = min(dp0, dp1) + cost[i];
        dp0 = dp1; // 记录一下前两位
        dp1 = dpi;
    }
    return min(dp0, dp1);
}

//每次爬楼梯方式与楼梯阶数一致
int nclimbStairs(int n) {
    vector<int> dp(n + 1, 0);
    dp[0] = 1;
    for (int i = 1; i <= n; i++) { // 遍历背包
        for (int j = 1; j <= i; j++) { // 遍历物品
            dp[i] += dp[i - j];
        }
    }
    return dp[n];
}

int main() {
    int n;  //共n阶台阶
    cin >> n;
    vector<int> cost(n);
    for (int i = 0; i < n; i++) {
        cin >> cost[i];
    }
    //int res = climbStairs(n);
    int res = minCostClimbingStairs(cost);
    //int res = nclimbStairs(n);
   
    cout << "爬n阶台阶方法数或体力花费最小数：" << res << endl;
    system("pause");
    return 0;
}