一、前言
堆是一种特殊的二叉树(完全二叉树),由于有堆排序等实际的需求,堆是由类似顺序表的结构实现的,这是为了方便堆能够通过下标找到parent和child,进行比较大小以及交换等操作。
1、BTNode结点的定义
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;这里我们建立二叉树的每个结点,包含左右孩子指针left和right,还有存储的数据data。
2、买(Buy)一个结点
BTNode* BuyBTNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (NULL == node)
{
perror("malloc fail");
return NULL;
}
node->data = x;
node->left = node->right = NULL;
return node;
}然后是得到新结点的BuyBTNode函数,得到一个新结点,检查后,将data赋值,为防止野指针,把left right置空,然后返回新结点。
3、简单的连接:CreateBTTree
BTNode* CreateBTTree()
{
BTNode* node1 = BuyBTNode(1);
BTNode* node2 = BuyBTNode(2);
BTNode* node3 = BuyBTNode(3);
BTNode* node4 = BuyBTNode(4);
BTNode* node5 = BuyBTNode(5);
BTNode* node6 = BuyBTNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
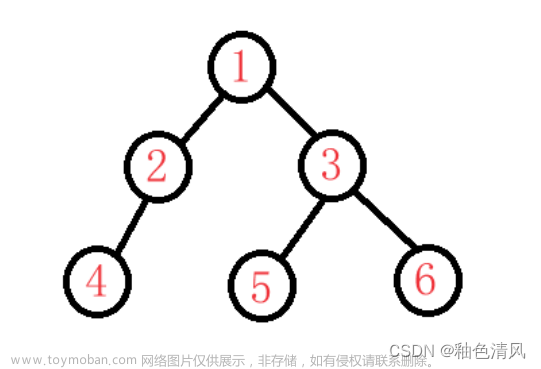
创建几个结点,并将它们连接后返回。
连接的结果如下。

二、前序遍历
首先要知道是,二叉树的前中后序遍历都是通过递归来实现的。顺序指的是根节点,和左右结点的访问顺序。
首先,前中后表示的是根节点的访问顺序是哪一个,其次左子结点的遍历默认先与右子结点。
前序遍历的访问顺序为:根节点、左子结点、右子结点。
//前序遍历 访问根(并打印显示) 左子树遍历 右子树遍历
void PrevOrder(BTNode* root)
{
//assert(root); NULL 作为递归结束标志,不能assert
if (NULL == root)
{
printf("NULL ");
return ;
}
printf("%d ", root->data);//打印来模拟访问根的过程
PrevOrder(root->left);//一棵树分为 根 左右子树 ,左右子树还可以拆,各自分成 根 左右子树,直到子树为NULL
PrevOrder(root->right);
}为了方便展示,这里我用打印来作为根访问的操作。

对于我之前创建的这棵树,递归的截止不是到最后一层的3/5/6结点,而是到它们的子树,即NULL
因此当root==NULL时,才开始结束这一层递归并往回返回。

先访问根节点,即打印1,然后进入PrevOrder(root->left),创建左子结点的函数栈帧,记为左子1
在左子1中,也是访问根节点,这里的根节点的值为2,然后再进入进入PrevOrder(root->left),也是创建左子结点的函数栈帧,记为左子2.
左子2中,访问根结点打印为3,重复上述操作,建立新函数栈帧,记为左子3.
对于左子3,它的值虽然是空,但因为同样调用的PrevOreder函数,因此同样需要创建函数栈帧,但是在这一层中,root为NULL,开始返回NULL。
返回后左子3的函数栈帧销毁,重新回到左子2函数内,执行完PrevOrder(root->left)后,应该执行的是PrevOrder(root->right),因此创建左子3的右子的函数栈帧,但因为同样为空,返回NULL。
这样一来,对于左子3,只剩最后的return root了,于是返回,并同时销毁左子3的函数栈帧。
回到左子2中,左子2的PrevOrder(root->left)操作结束,进入PrevOrder(root->right)操作,建立函数栈帧,为NULL返回,然后左子2中只剩下return root,于是返回左子2,然后销毁左子2。
回到左子1即(值为2的结点),此时PrevOrder(root->left)已经结束,即原来的根节点访问,和左子结点访问都结束了,开始进入右子结点的访问,对于右子结点,大家可以自己推导。

三、中序遍历

与前序遍历类似,同样使用递归展开。
中序遍历访问顺序:左子结点、根结点、右子结点。
实现代码中,把打印和InOrder(root->left)的位置互换,使其先访问左子结点,然后再是根节点。


先是连续的几次InOrder(root->left)的访问,直到左子2(值为3),然后继续访问其左子树,建立左子3的函数栈帧,打印NULL后销毁函数栈帧,然后返回到左子2.
左子2中,InOrder(root->left)已经结束,于是开始访问根节点,即打印3,然后再进行InOrder(root->right),访问右子结点,打印NULL后返回,此时左子2已经结束返回到左子1。
然后重复递归操作,完成中序遍历。

上图为具体的递归展开图,可以画图参考。
四、后序遍历
访问顺序为:左子结点、右子结点、根结点。
与前面类似,这里不做详细解释。


五、求总结点数
//返回总的结点个数 == 左子树结点个数+右子树结点个数+1 也可以多加一个int*size参数,函数内部改变外部的这个变量
int TreeSize(BTNode* root)
{
return NULL == root ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
//if (NULL == root)
//{
// return 0;
//}
//return TreeSize(root->left) + TreeSize(root->right) + 1;
}可以采用返回值的方式,在最开始的一层栈帧中返回总个数,在外面用变量接收。
也可以在外面创建变量,传入地址,在递归过程中不断修改这个变量。
最好不要在外面使用全局变量size,否则,如果多次调用TreeSize函数而不 置为0,就会一直累加
与前中后序遍历相同,一直遍历到左子3,因为是NULL,所以返回的是0,对于左子2(值为3),其TreeSize(root->left)和TreeSize(root->right)均为0,所以它返回给上一层的是0+0+1(自身)。
因此通过递归后,得到 左子树结点数+右子树结点数+1就得到了这棵树的总结点数。

文章来源地址https://www.toymoban.com/news/detail-403570.html
六、求树的高度/深度(起始为1)

与TreeSize类似,递归到最后一层时返回0,先得到左右子树各自的层数,然后比较它们中较大的那个,返回时,用较大的值+1(自身这一层),最终得到树的高度。
这里最好是用leftheight和rightheight保存一下,否则使用三目操作符返回时会产生重复递归,使得时间复杂度异常增大。

七、查找第K层结点的个数

对于我之前创建的这颗树,我们可以很轻易地知道,设k为层数,n为该层的结点数
当k=1时,n=1. 当k=2时, n=2. 当k=3时, n=3
这是因为结点总数较少,我们可以轻易地数出来。但是怎样利用递归让计算机帮我们求解呢?
二叉树递归的核心就是分治思想,上面是根,下面是左子树和右子树,我们如何把任务从n变成n-1
再变成n-2,……直到转换为n=1或n=0的情况呢?
可以使用一个相对的思想。先从第一层看起,要求它第k层的总数,转换为它的左右子结点的第k-1层的元素总数。
例如:对于1这个元素,求它的第三层的元素数,可以转化为求2和4这两个元素,它们的第3-1=2层的结点总数。再转化为2和4各自的左右子结点的2-1=1层的结点总数,也就是它们自身这一层的结点数。
代码实现如下:

如果根为空,(这个根可以是之前根的左右子树通过递归得到的),这时求它的第k或k-1层的结点数肯定是0,所以可以直接返回0即可。
需要注意的是:这里需要额外判断k==1的情况,也就是该层的元素是多少,对于任何一个存在,并且求它k==1时的结点,得到的答案都是1。
换种说法,也就是从k==1层开始才能返回非0值。
这里简单说一下递归展开的过程:前面因为没有遇到空,便一直开辟函数栈帧,因为默认左边先于右边访问,最先达到返回条件的是val=3的这个结点,(与之前不同,这里不用等到3的下一层再返回,当k==1时也可以返回),对于3这个结点,直接返回1给上一层val=2的结点作为leftsize。
然后是3的右兄弟,为空返回0,这样就拿到2这个结点的第2层共1+0=1个结点了。
而对于旁边的5和6,各自返回1, val=4的这个结点拿到1+1=2,然后 2和4各自返回,到最初的val=1的根节点,leftsize=TreekLevel=1,rightsize=TreekLevel=2。最终返回3.

八、查找值为x的结点

如果根为空,直接返回NULL,找到x时返回root,指向该结点的指针。
都没找到就往它的左右子结点找,只要找到就返回,不进行后续操作,没找到就继续,如果左右都找不到说明该root指向的树没有这个数据。
 找的时候一层一层建立栈帧找,找到或找不到后,快速返回。
找的时候一层一层建立栈帧找,找到或找不到后,快速返回。

找到5返回其地址,找不到50,返回NULL
九、层序遍历

层序遍历是从最初的根节点从上向下,从左到右依次访问。

我们可以借助队列先进先出的性质帮助我们完成。
先Push最初的元素,对于其它元素,只要Pop就把它的左右子结点都Push到队列中(因为放进去之后,拿出来时要依次访问的结果是一个个数据,因此就没有必要把NULL放入了)。
对于1:Pop后Push 2 4,再Pop2,进入3,此时队列为 4 3,再Pop4,Push5,6。
此时队列中为3 5 6,再依次Pop拿出来即可。

首先:由于队列中要存储的是二叉树的结点,要typedef一下QueueDataType,因为结点所占空间较大,我们直接存储指向的结点指针。
先用front接收队头的位置,打印后,利用QueuePop删除队头的元素(实际上是改变这个Queue队列头指针的指向,并且把要删除的那个队列的结点给free掉,这个结点存储的不是二叉树结点,只是它的指针,因此free后对二叉树的结点无影响)。
但因为我们事先用front保存了队列头结点的值,即二叉树结点的指针,我们可以直接用front->left和front->right找到它的两个子结点,然后再将子节点入队列。
当然,最后不要忘了destroy一下之前创建的队列。

十、判断二叉树是否是完全二叉树
这里需要运用之前的层序遍历。

观察可以发现,对于完全二叉树,空结点和非空结点是有明确界限的,出现了空节点后,后面的所有结点一定都是空节点,不会再出现非空结点。
所以应该用得到第一个NULL,并对后面节点进行遍历,查找是否还有非空结点来判断是否完全。
所以空节点也要入队列。

先进行找空的操作,找到后break,再在剩余元素中找非空,找到非空return false,全部出队列后依然没找到,则返回true。
注意返回前要检查是否已经销毁。

最初创建的树不是完全二叉树,返回false即0.
新增了一个node7,并将其连接在val=2的位置上后形成了完全二叉树,返回true即1.
十一、 二叉树的销毁
//二叉树的销毁
void BTDestroy(BTNode* root)
{
if (NULL == root)
return;
BTDestroy(root->left);
BTDestroy(root->right);
free(root);
}通过递归销毁即可。
十二、总结
二叉树有几个关键点。
1、一个是分治思想,这决定了递归的实现。如何通过root,建立root->left,root->right的关系。
怎么样从n变成n-1变成n-2,直到变成1或0。
2、对于DFS,递归的具体顺序是什么,结合函数栈帧的创建与销毁,是一路递归,两路递归,还是多路递归。
本文一共5000多字,现在是早上5点半了,希望大家早上起来能够支持一下吧,你们的支持和鼓励就是我最大的动力。


目录
一、前言
1、BTNode结点的定义
2、买(Buy)一个结点
3、简单的连接:CreateBTTree
二、前序遍历
三、中序遍历
四、后序遍历
五、求总结点数
六、求树的高度/深度(起始为1)
七、查找第K层结点的个数
八、查找值为x的结点
九、层序遍历
十、判断二叉树是否是完全二叉树
十一、 二叉树的销毁
十二、总结文章来源:https://www.toymoban.com/news/detail-403570.html
到了这里,关于二叉树BFS/DFS及重要递归接口--拿下二叉树--拿下数据结构--拿到好offer的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!