提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
前言

ChatGPT一问世就给整个社会带来巨大的震撼和冲击,不禁让人惊叹现在AI的强大,我们好像离通用人工智能更近一步。在过去十几年人工智能领域的蓬勃发展中,扮演着主导地位的算法基本都是神经网络和深度学习,很多机器学习算法黯然失色。神经网络和深度学习虽然强大,但这个"黑盒"里面到底是个什么东西我们很难解释,就像人脑一样,神经元之间的相互作用是非常复杂微妙的。那机器学习中有没有一种比较强大的模型但是又可以很好解释的呢?有,那就是集成学习算法随机森林,而随机森林的每个分类器个体就是我们今天的主角- -决策树。
一、决策树算法简介

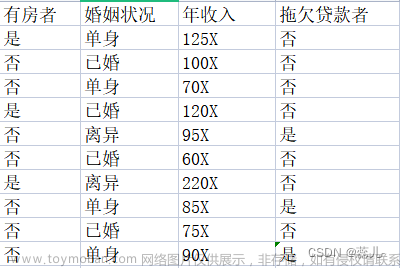
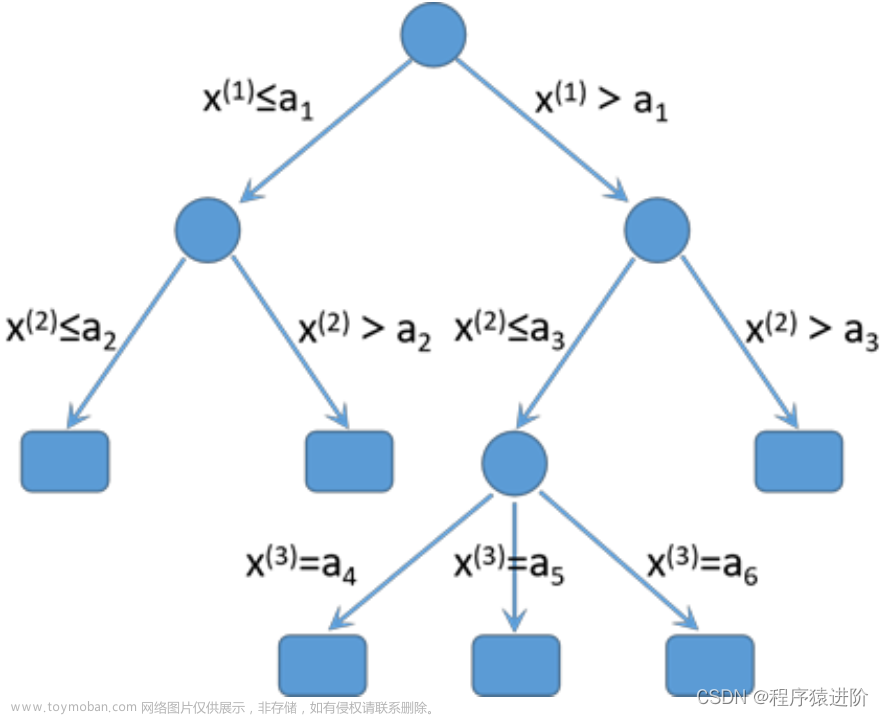
决策树算法是一种常用的有监督学习的机器学习算法,是一种以树结构(包括二叉树和多叉树)形式来表达的预测分析模型。树是一种特殊的数据结构,是一种有向无环图,即树是有方向但没有形成闭环回路的图形,主要作用是分类和遍历。决策树利用分类的思想,根据数据的特征构建数学模型,从而达到数据的筛选,并完成决策的目标。决策树中每个节点表示某个特征对象,而每个分叉路径则代表某个可能的分类方法,而每个叶节点则对应从根节点到该叶节点所经历的路径所表示的对象的值。
二、决策树的数学原理
决策树算法是以分类为目的的模型,这种分类旨在降低每个类里面样本标签的熵值,即让该类中的样本数据的标签更加一致,经过转化我们也可以将决策树算法应用于解决回归预测的问题中

1. 熵的度量
熵是表示随机变量不确定性的度量,事物的熵越大表示事物的混乱程度越大,事物的熵越小表示事物的混乱程度越小,在物理世界中熵总是朝着增大的方向进行。决策树中我们借助熵来衡量分类后叶子节点的样本标签的混乱程度,我们希望分支节点的熵值越低越好,
这样才能在后续叶子节点的决策中达到不错的效果

在决策树的分支节点中,我们依据古典概型,即用随机变量所占的比例来衡量它发生的概率,将概率值转化为信息熵,
H
(
X
)
H(X)
H(X) 表示信息熵值
H
(
X
)
=
−
∑
i
=
1
n
p
i
l
o
g
(
p
i
)
H(X) = -\sum_{i=1}^np_{i}log(p_{i})
H(X)=−i=1∑npilog(pi)
除了经典的信息熵应用,我们有时也会涉及到条件熵的概念。条件熵和信息熵的关系就好像条件概率和概率的关系,条件熵强调了对一定条件下事物的不确定性度量,
H
(
Y
∣
X
)
H(Y | X)
H(Y∣X) 表示条件熵
H
(
Y
∣
X
)
=
∑
i
=
1
n
p
i
H
(
Y
∣
X
=
x
i
)
H(Y | X) = \sum_{i=1}^np_{i}H(Y | X=x_{i})
H(Y∣X)=i=1∑npiH(Y∣X=xi)
H
(
Y
∣
X
=
x
i
)
=
∑
j
=
1
n
p
(
y
j
∣
x
=
x
i
)
l
o
g
(
p
(
y
j
∣
x
=
x
i
)
)
H(Y | X=x_{i}) = \sum_{j=1}^n p(y_{j} | x=x_{i}) log(p(y_{j} | x=x_{i}))
H(Y∣X=xi)=j=1∑np(yj∣x=xi)log(p(yj∣x=xi))
一般我们在计算 H ( Y ∣ X = x i ) H(Y | X=x_{i}) H(Y∣X=xi) 时我们通过缩小样本空间,用古典概型来计算。当熵和条件熵中的概率由数据估计(特别是极大似然估计)得到时,所对应的熵与条件熵分别称为经验熵(empirical entropy)和经验条件熵(empirical conditional entropy)。

根据熵值的函数 p i l o g p i p_{i}logp_{i} pilogpi的图像,当随机变量的概率值趋近于1或者0时,即该集合中基本上都是这个变量或者基本上不存在这个变量,那表示该集合不确定性很低,此时函数值趋近0,熵值趋近0,集合内的标签很有序;当随机变量的概率值分布在0到1中间时,即该集合中有这个变量并且还有其他变量,那表示该集合不确定性很高,此时熵值较大,集合内的标签混乱无序
2. 信息增益
决策树模型中常见的三种算法有:ID3、C4.5、CART。ID3算法是以信息增益为标准来度量在不同的节点特征选择下哪种方案是最优的,即用循环的方式选择出信息增益最大的节点特征然后这样递归下去形成决策树,用特征
a
a
a 对样本集
D
D
D 进行划分所获得的“信息增益”可以表达为:
I
n
f
o
G
a
i
n
(
D
∣
a
)
=
H
(
D
)
−
H
(
D
∣
a
)
InfoGain(D|a) = H(D) - H(D | a)
InfoGain(D∣a)=H(D)−H(D∣a)
然后我们选择信息增益最大的特征节点,然后递归去遍历下一个节点。简单来说,我们用信息增益方法来达到节点标签更加有序的效果,增强叶子节点的确定性,就像购物网站对商品进行分类,先分数码区用品,生活用品等,再按品牌或者价格进行分类

C4.5算法是用信息增益率来作为标准,比ID3算法多考虑了自身熵值存在的影响,假如决策树分的类别越多,分到每一个子结点,子结点的纯度也就越可能大,因为数量少了嘛,可能在一个类的可能性就最大,甚至可以一个叶子节点就一个标签值,但这样会使决策树模型过拟合,所以我们引入自身属性的考量降低过拟合风险
G
a
i
n
R
a
t
i
o
(
D
∣
a
)
=
−
I
n
f
o
G
a
i
n
(
D
∣
a
)
H
(
D
∣
a
)
GainRatio(D|a) = -\frac{InfoGain(D|a)}{H(D | a)}
GainRatio(D∣a)=−H(D∣a)InfoGain(D∣a)

CART算法中节点标签的纯度可用基尼值来度量,基尼系数反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率。因此,基尼系数越小,则节点的纯度越高
G
i
n
i
(
p
)
=
∑
k
=
1
n
p
k
(
1
−
p
k
)
Gini(p) = \sum_{k=1}^np_{k}(1-p_{k})
Gini(p)=k=1∑npk(1−pk)
3. 剪枝策略
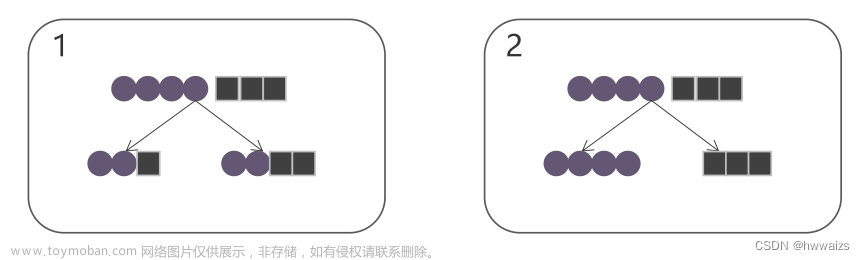
剪枝策略旨在降低决策树过拟合的风险,限制决策边界过于复杂,说白了就是你家花园里的树木枝叶太多过于庞大,这时你就需要给这些枝叶修剪一下,使这棵树看起来更加精神,更有活力

决策树的剪枝策略分为预剪枝和后剪枝,预剪枝比较简单,就是在决策树生成前限制树的深度和叶子节点的个数,避免出现一个叶子节点一个标签值的情况出现,相当于你家的树一边生长你一边修理枝叶

决策树的后剪枝是在决策树生成后再对树模型进行剪枝,代价复杂度剪枝-CCP用 C ( T ) C(T) C(T) 作为损失函数衡量决策树的效果,其中 T T T 是叶子节点数。这里面涉及到一个重要参数 α \alpha α, α \alpha α 是自己给定的, α \alpha α 越大则表示你越不希望树模型过拟合, α \alpha α 越小则表示你越希望决策树的分类效果好,即叶子节点的纯度越高
三、Python实现决策树算法
1. CART决策树
Python实现决策树算法的思路也和前面一样,先导入常用的包和鸢尾花数据集,接着选择鸢尾花数据的几个特征和标签并将决策树实例化,训练决策树,然后用graphviz工具展示决策树,并用matplotlib绘制棋盘和决策边界,最后展示一下
import numpy as np
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
from IPython.display import Image
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
iris = load_iris()
x = iris.data[:, 2:]
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2)
tree_clf.fit(x, y)
def plot_decision_boundary(clf, x, y, axes=[0, 7.5, 0, 3]):
x1a = np.linspace(axes[0], axes[1], 100)
x2a = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1a, x2a)
x_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(x_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#fafab0', '#9898ff', '#507d50'])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
plt.plot(x[:, 0][y == 0], x[:, 1][y == 0], "yo", label="Iris-Setosa")
plt.plot(x[:, 0][y == 1], x[:, 1][y == 1], "bs", label="Iris-Versicolor")
plt.plot(x[:, 0][y == 2], x[:, 1][y == 2], "g^", label="Iris-Virginica")
plt.axis(axes)
plt.xlabel("Petal length", fontsize=12)
plt.ylabel("Petal width", fontsize=12)
export_graphviz(tree_clf, out_file="iris_tree.dot", feature_names=iris.feature_names[2:], class_names=iris.target_names, rounded=True, filled=True )
plt.figure(figsize=(12, 8))
plot_decision_boundary(tree_clf, x, y)
plt.plot([2.45, 2.45], [0, 3], "k-", linewidth=2)
plt.plot([2.45, 7.5], [1.75, 1.75], "k--", linewidth=2)
plt.plot([4.95, 4.95], [0, 1.75], "k:", linewidth=2)
plt.plot([4.85, 4.85], [1.75, 3], "k:", linewidth=2)
plt.text(1.4, 1.0, "Depth=0", fontsize=15)
plt.text(3.2, 1.8, "Depth=1", fontsize=13)
plt.text(4.05, 0.5, "Depth=2", fontsize=11)
plt.title('Decision Tree')
plt.show()

可以看到决策树通过
G
i
n
i
Gini
Gini 系数作为判定节点分类的效果的标准,先以花瓣宽度0.8作为边界将第一类花完全分开,接着以花瓣宽度1.75作为花瓣的宽度基本将剩下两种花分开

2. 决策树剪枝对比
Python实现决策树剪枝对比的思路也和前面一样,先导入常用的包和月亮数据集,指定月亮数据集的样本数和噪音率,接着将决策树实例化并训练决策树,然后用用matplotlib绘制棋盘和决策边界,最后用两幅子图展示一下两种不同的效果
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.tree import DecisionTreeClassifier
from matplotlib.colors import ListedColormap
x, y = make_moons(n_samples=200, noise=0.3, random_state=50)
tree_clf1 = DecisionTreeClassifier(random_state=50)
tree_clf2 = DecisionTreeClassifier(min_samples_leaf=9, random_state=50)
tree_clf1.fit(x, y)
tree_clf2.fit(x, y)
def plot_decision_boundary(clf, x, y, axes=[0, 7.5, 0, 3]):
x1a = np.linspace(axes[0], axes[1], 100)
x2a = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1a, x2a)
x_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(x_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#fafab0', '#9898ff', '#507d50'])
plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
plt.plot(x[:, 0][y == 0], x[:, 1][y == 0], "yo", label="Iris-Setosa")
plt.plot(x[:, 0][y == 1], x[:, 1][y == 1], "bs", label="Iris-Versicolor")
plt.plot(x[:, 0][y == 2], x[:, 1][y == 2], "g^", label="Iris-Virginica")
plt.axis(axes)
plt.xlabel("Petal length", fontsize=12)
plt.ylabel("Petal width", fontsize=12)
plt.figure(figsize=(12, 8))
plt.subplot(121)
plot_decision_boundary(tree_clf1, x, y, axes=[-1.5, 2.5, -1, 1.5])
plt.title("No restrction")
plt.subplot(122)
plot_decision_boundary(tree_clf2, x, y, axes=[-1.5, 2.5, -1, 1.5])
plt.title("min_slamples=9")
plt.show()

我们可以看到没有经过剪枝的决策边界显得十分复杂,过拟合风险极高;而经过剪枝和规定最小叶子节点样本数的决策边界相对简单,过拟合风险较低,而且在处理噪音点这方面表现不错文章来源:https://www.toymoban.com/news/detail-403612.html
总结
以上就是机器学习中决策树算法的学习笔记,本篇笔记简单地介绍了决策树的数学原理和程序思路。决策树算是机器学习中非常容易解释的一种模型,下次笔记里的机器学习集成算法随机森林也是对决策树的一种拓展和延伸,集成算法在深度学习得到广泛吹捧的今天仍然有一席之地,离不开决策树强大的可解释性和泛化能力。文章来源地址https://www.toymoban.com/news/detail-403612.html
到了这里,关于Python 机器学习入门 - - 决策树算法学习笔记的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!