1.卡方分布
在统计学中, 很多假设检验的检验统计量在原假设下服从卡方分布. 这种检验统计量服从卡方分布的假设检验适用于分类数据.
Γ
(
v
2
)
\Gamma(\frac{v}{2})
Γ(2v)为伽马函数
检验此PDF的积分值是否为1？
自由度（DoF）的正式定义为统计学中可以自由变化的数值个数. 如果有 N 个观测值,那么自由度通常是 N − 1 或 N.
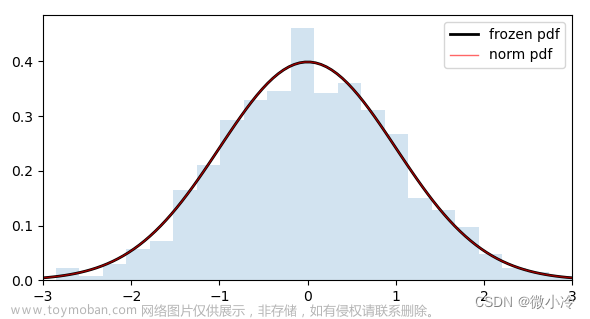
1.1 卡方分布与标准正态分布的关系
服从标准正态分布的随机变量服从自由度为1的卡方分布
1.2 计算自由度为 k = 1 的卡方分布的均值、方差
均值
方差
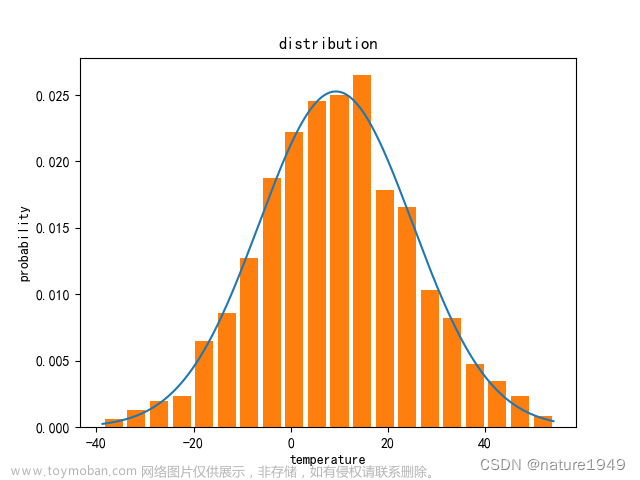
1.3 卡方分布与服从正态分布的随机变量之和
1.4 卡方检验
卡方检验的优点是它是一个非参数检验. 具体地说, 这意味着它对提取数据的基本总体分布没有任何假设.
卡方检验的的缺陷要比其他参数检验的统计效果差.
有三种不同类型的卡方检验在应用中非常重要
1.卡方拟合优度检验的解释, 它用来衡量一组分类数据是否来自某个特定的离散分布
2.卡方齐性检验, 它应用于来自多个不同总体的单个分类变量, 并检验该变量的频率计数在不同总体中是否有统计学差异. 换句话说, 卡方齐性检验用来测试不同总体的频率计数是否服从同一种分布
3.卡方独立性检验, 它应用于来自同一总体的多个分类变量, 并确定变量之间的关联是否具有统计学意义. 换言之, 卡方独立性检验考察的是变量之间是否存在独立性.
计算检验统计量
例子：文章来源：https://www.toymoban.com/news/detail-404039.html
文章来源地址https://www.toymoban.com/news/detail-404039.html
到了这里，关于卡方分布（Chi-Square Distribution）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
