在这组题(蓝桥杯C/C++ B组 国赛)里面挑了几道喜欢的题目,做了一下,笔记思路如下。(其实是我觉得能做出的题 )
题目图片来源于:CSDN 罚时大师月色
A:2022
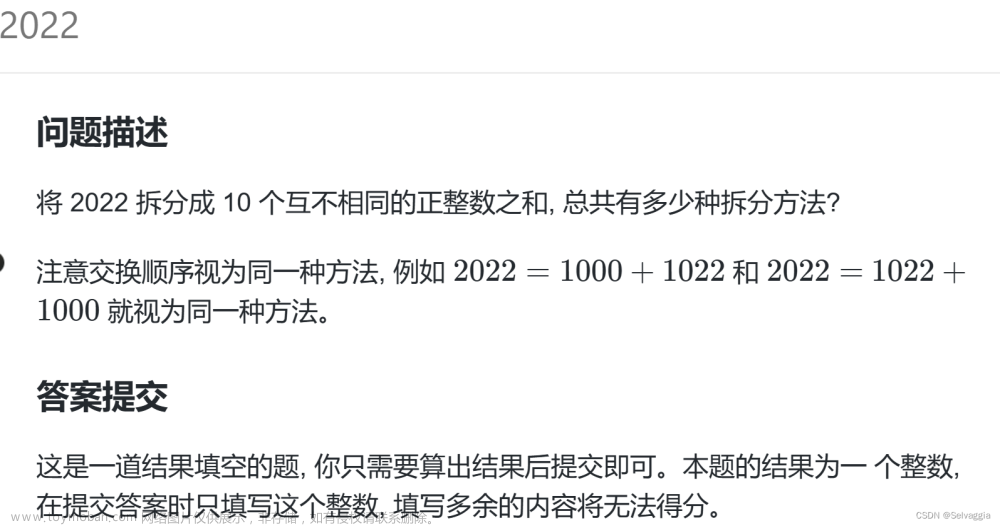
【题目大意】
请问2022,拆分成10个不同的正整数有多少种不同的分法。
【解析】
这道题目,拿到手上的时候,第一个想法是暴力,但是,每次分别枚举10位上,到底数字是多少,比如,每一位枚举从1->200,那么复杂度是
O
(
20
0
10
)
O(200^{10})
O(20010)。这个复杂度已经上天了。
但是我想应该还是有,暴力的方法,因为可以每次暴力分成两半?让我再想想这个暴力算法。
正解是,首先使用搜索,对于每一个位置进行搜索。rec(int i,int num,int sum);
考虑第i项目(1->i项,比如题目有10位,那么我们就有10个项要填写),在当前项填入的数字为num的时候,它和前一项填入的数字有关,例如,当我们在第i项填写了num,那么前i-1项加起来,应该总和为sum-num。
举个栗子:rec(3,5,10)=rec(2,4,10-5)+rec(2,3,10-5)+rec(2,2,10-5)+rec(2,1,10-5)
注意第二个参数,它从4,3,一直变成了1,这是在搜索,第二个位置,填入4,3…1,总和为10-5的方案数,rec(3,5,10)依赖于他们。那么,中间这个参数可以为5,或6…other 吗?不可以的,因为我们想要严格地使得,我们所搜索地数字,按照严格递增排列,所以,前一个数字,不可以大于我们当前位置上地数字。
所以,我们现在可以写出如下的代码:
typedef long long LL;
static LL dp[12][2024][2024];
int n = 2022, c = 10;
LL rec(int i, int num, int sum) {
if (dp[i][num][sum] >= 0) { //记忆化搜索部分
return dp[i][num][sum];
}
if (i == 1 && sum != num || num <= 0 || sum <= 0) {
return dp[i][num][sum] = 0;
} else if (i == 1 && sum == num) {
return dp[i][num][sum] = 1;
}
LL ans = 0;
for (int j = 1; j < num; j++) { // 在进入的时候,已经保证了,j < num,*****我们在这里循环了******
ans += rec(i - 1, j, sum - num);
}
return dp[i][num][sum] = ans;
}
但是这样的算法复杂度和变量参数变化有关,为
i
∗
n
u
m
∗
s
u
m
i*num*sum
i∗num∗sum,然后在函数内部我们又进行了一次num的循环,所以是
i
∗
n
u
m
∗
s
u
m
∗
n
u
m
i*num*sum*num
i∗num∗sum∗num,为
c
∗
n
∗
n
∗
n
c*n*n*n
c∗n∗n∗n
复杂度依旧上天。
让我们来考虑一下,还有什么地方可以被优化吗?
r
e
c
(
3
,
5
,
10
)
=
r
e
c
(
2
,
4
,
10
−
5
)
+
r
e
c
(
2
,
3
,
10
−
5
)
+
r
e
c
(
2
,
2
,
10
−
5
)
+
r
e
c
(
2
,
1
,
10
−
5
)
rec(3,5,10)=rec(2,4,10-5)+rec(2,3,10-5)+rec(2,2,10-5)+rec(2,1,10-5)
rec(3,5,10)=rec(2,4,10−5)+rec(2,3,10−5)+rec(2,2,10−5)+rec(2,1,10−5)
之前的这个式子,观察第2项到末尾项。
即如下:
r
e
c
(
2
,
3
,
10
−
5
)
+
r
e
c
(
2
,
2
,
10
−
5
)
+
r
e
c
(
2
,
1
,
10
−
5
)
rec(2,3,10-5)+rec(2,2,10-5)+rec(2,1,10-5)
rec(2,3,10−5)+rec(2,2,10−5)+rec(2,1,10−5)
这些项目其实就是
r
e
c
(
3
,
5
−
1
,
10
−
1
)
rec(3,5-1,10-1)
rec(3,5−1,10−1)!!!
所以,我们之前的这个:
r
e
c
(
3
,
5
,
10
)
=
r
e
c
(
2
,
4
,
10
−
5
)
+
r
e
c
(
2
,
3
,
10
−
5
)
+
r
e
c
(
2
,
2
,
10
−
5
)
+
r
e
c
(
2
,
1
,
10
−
5
)
rec(3,5,10)=rec(2,4,10-5)+rec(2,3,10-5)+rec(2,2,10-5)+rec(2,1,10-5)
rec(3,5,10)=rec(2,4,10−5)+rec(2,3,10−5)+rec(2,2,10−5)+rec(2,1,10−5)
可以写成这个:
r
e
c
(
3
,
5
,
10
)
=
r
e
c
(
2
,
4
,
10
−
5
)
+
r
e
c
(
3
,
5
−
1
,
10
−
1
)
rec(3,5,10)=rec(2,4,10-5)+rec(3,5-1,10-1)
rec(3,5,10)=rec(2,4,10−5)+rec(3,5−1,10−1)
我们从数学的角度尝试了简化。但是其实我们也可以从含义的角度进行简化:
对于一般的
d
p
[
i
]
[
n
u
m
]
[
s
u
m
]
dp[i][num][sum]
dp[i][num][sum]。我们可以有这样的考虑:
(1)魔改
d
p
[
i
]
[
n
u
m
−
1
]
[
s
u
m
−
1
]
dp[i][num-1][sum-1]
dp[i][num−1][sum−1]:对于有i项,并且第i项是num-1,总和为sum-1,所以我们可以在这个基础之上,直接把末尾的num-1变成num直接就满足我们想要的邪恶内容了,Perfect。
(2)转移
d
p
[
i
−
1
]
[
n
u
m
−
1
]
[
s
u
m
−
n
u
m
]
dp[i-1][num-1][sum-num]
dp[i−1][num−1][sum−num]:从i-1的末尾状态上,接入我们的num,这也是(1)中可能会漏掉的情况,为什么,比如我们有:
n=10 c=3
即:
1 2 7
1 3 6
1 4 5
2 3 5
末尾为5的可以从2 3 4魔改4变成5 但是无法从1 4 4把末尾4魔改成5。因为1 4 4根本不存在,所以,我们有了
d
p
[
i
−
1
]
[
n
u
m
−
1
]
[
s
u
m
−
n
u
m
]
dp[i-1][num-1][sum-num]
dp[i−1][num−1][sum−num]把num-1,sum-num,i-1接上去试一试有没有这种状态。就补足了(1)中的空缺。
LL rec(int i, int num, int sum) {
if (dp[i][num][sum] >= 0) { //记忆化搜索部分
return dp[i][num][sum];
}
if (i == 1 && sum != num || num <= 0 || sum <= 0) {
return dp[i][num][sum] = 0; //num为0,不可能有成功的状态了,所以到达我们时候,num为0,直接return 0。或者i==1时候,如果填入的num,不能满足总和为sum,那么一定是错的,比如rec(1,2,3),只有一个位置,填2怎么填都不可能配出3来的
} else if (i == 1 && sum == num) {
return dp[i][num][sum] = 1;//i==1,并且现在填入的数字,就是我们要配出的sum总和,那么就完全O98K。
}
LL ans = 0;
// for (int j = 1; j < num; j++) { // 在进入的时候,已经保证了,j < num
// ans += rec(i - 1, j, sum - num);
// }
//如果使用For的话,那每一层都会for一次,对应DP就要多一次循环,优化思路是减少这个for
ans += rec(i, num - 1, sum - 1);
ans += rec(i - 1, num - 1, sum - num);
return dp[i][num][sum] = ans;
}
我们有了记忆化搜索的思路,那么动态规划也就手到擒来了。
想想我们回溯的过程,我们从i==1开始,往i大的方向回溯。
从num小的时候,向num大的时候回溯,sum也是。
下面直接给出动态规划的代码:
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
typedef long long LL;
static LL dp[12][2030][2030];
LL ans = 0;
int n = 2022, c = 10;
int main() {
memset(dp, 0, sizeof(dp));
dp[0][0][0] = 1;
for (int i = 1; i <= c; i++) {
for (int num = 1; num <= n; num++) {
for (int sum = num; sum <= n; sum++) { //总和不可能小于所填写的数字
dp[i][num][sum] = dp[i][num - 1][sum - 1] + dp[i - 1][num - 1][sum - num];
if (i == c && sum == n) { //把答案加起来
ans += dp[i][num][sum];
}
}
}
}
cout << ans << endl;
return 0;
}
这段代码的意思是:
if (i == c && sum == n) { //把答案加起来
ans += dp[i][num][sum];
}
考虑所有的 d p [ c ] [ ∗ ] [ n ] dp[c][*][n] dp[c][∗][n]方案数总和,就是*为末尾数字,不停探索,符合 i = = c ∩ s u m = = n i==c \cap sum==n i==c∩sum==n的方案。不理解,可以看看下面记忆化搜索全代码。
记忆化搜索全代码:
//这里是记忆化搜索(正确)
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
typedef long long LL;
static LL dp[12][2024][2024];
int n = 2022, c = 10;
LL rec(int i, int num, int sum) { //这修改后,去除了right(小熊写的时候,纯呼呼判断了右侧数字,但其实没必要,看下文代码)
if (dp[i][num][sum] >= 0) { //记忆化搜索部分
return dp[i][num][sum];
}
if (i == 1 && sum != num || num <= 0 || sum <= 0) {
return dp[i][num][sum] = 0;
} else if (i == 1 && sum == num) {
return dp[i][num][sum] = 1;
}
LL ans = 0;
// for (int j = 1; j < num; j++) { // 因为在进入的时候,已经保证了,j < num
// ans += rec(i - 1, j, sum - num);
// }
//如果使用For的话,那每一层都会for一次,对应DP就要多一次循环,优化思路是减少这个for
ans += rec(i, num - 1, sum - 1);
ans += rec(i - 1, num - 1, sum - num);
return dp[i][num][sum] = ans;
}
int main() {
memset(dp, -1, sizeof(dp));
LL ans = 0;
for (int i = 1; i <= n; i++) {
ans += rec(c, i, n);
}
cout << ans;
return 0;
}
//rec(当前到了第i处(下标从1开始),这处填的数字,这处总和加起来是)。
//rec(i,num,sum)=res(i-1,j,sum-num)方案数; j从1到num-1,这样保证i-1处的j总是小于i处的num。
//通过观察可以发现,res(i-1,num-1,sum-num)+res(i-1,num-2,sum-num)+...+res(i-1,1,sum-num)。
//这一段,实际上就是res(i,num-1,sum-1),这样一来,就可以去除掉一个for循环,时间复杂度又降低了一个维度,使得题目可以做出。
//也可以直接从含义上理解dp[i][num][sum]=dp[i][num-1][sum-1]+dp[i-1][num-1][sum-num]
//就是,从第i项,放置数字为num,总和为sum,分为两个角度(1)直接从第i项,第i项数字为num-1,总和为sum-1的地方魔改,这样,把末尾数字+1,则可以直接满足题目的要求了。(2)从第i-1项的末尾进行拼接,我们现在状态是第i项为num,总和为sum,所以从dp[i-1][num-1][sum-num]处拼接就可以啦。num-1是要求末尾小一点,sum-num是还剩余你i-1要凑出的数字。而dp[][][]就是方案数。
//我们换种说法,比如现在我们有第i项是5,那么第i-1项如果是4,那么x x 4 5这个万一是符合答案的就会在(2)中漏掉。(1)就是为了看看我们有没有漏掉这种情况。而x x 3 4加起来等于sum-1,就不会漏掉,一个例子是n=10,c=3。则有1 4 5、2 3 5。其中2 3 5在2 3 4==9中属于(1)被加入到了答案中,而1 4 5 属于(2)的情况,被加入到了答案中。
//无论是先从i项考虑到i-1项,还是通过考虑魔改,最后答案的动态规划式都是一样的。
//从运行速度来说,记忆化搜索,和写for循环的动态规划,时间复杂度差不多,最主要在于空间复杂度。
两个写法最后答案都是对的。
——————————————————
二更
考虑10 3:
1 2 7
1 3 6
1 4 5
2 3 3
当每一位都减去1的时候
0 1 6
0 2 4
0 3 4
1 2 2
所以其实dp[3][10]=dp[3][7]+dp[2][7]
即1 2 2是dp[3][7] 而这一位减完变成开头的则是dp[2][7]
只要dp计算的是正确的(即每一位都是按照大小排列的,那么这个算法就不会有问题)
更一般的递推等式:dp[m][n]=dp[m][n-m]+dp[m-1][n-m]文章来源:https://www.toymoban.com/news/detail-404167.html
AC代码:文章来源地址https://www.toymoban.com/news/detail-404167.html
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
long long dp[13][2077];
int m = 10, n = 2022;
int main() {
memset(dp, 0, sizeof(dp));
fill(&dp[1][1], &dp[1][2077], 1);
for (int i = 2; i <= m; i++) {
for (int j = 3; j <= n; j++) {
dp[i][j] = dp[i][j - i] + dp[i - 1][j - i];
}
}
cout << dp[m][n];
return 0;
}
B:以后再写
到了这里,关于题解动态规划:蓝桥杯2022国赛B组 题解 A题目的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!