笔者最近在学习有关多目标优化的内容,并对内容进行一些整理。这篇文章算是笔者的一篇个人学习笔记,也希望能对他人提供一定的帮助,若有不足之处,也欢迎指正和建议。
注:本文中所举例子均为最小化问题。
一.多目标优化的基本概念
(1) 多目标优化问题(Multiobjective optimization problem,MOP)
一个多目标优化问题可以用下面的数学形式来表述:
![[多目标优化算法]1.NSGA-II——非支配排序遗传算法](https://imgs.yssmx.com/Uploads/2023/04/404492-1.png)
其中,x为决策向量,所在空间称为决策空间;F(x)为目标向量,所在空间称为目标空间,由m个目标函数组成,在多目标优化中,m一般为2或3,相对应的,单目标优化的m=1.
(2) 支配(Dominance)
对于两个解x与y,若对于任意i=1,2,...,m,均有fi(x)<=fi(y),且存在i,使fi(x)<fi(y), 则称x支配y,记为。
简单记忆方法:全部小于等于,至少1个小于。
(3) Pareto最优
Pareto最优原为经济学中的一个概念,在多目标优化中,由于对于不同目标的优化通常是互相矛盾的,故引入该概念。在多目标优化中,若对于解x*,当且仅当x*不被任何其他解支配,称x*为Pareto最优解,由所有Pareto最优解构成的集合,称为Pareto集(Pareto Set),记为PS。相对应的,PS中所有解在目标空间中对应的目标函数值的集合称为Pareto前沿(Pareto Front),记为PF。
(注意,Pareto最优的概念仅是说该解不被其他解支配,并不是说该解可以支配其他所有解。)
二.NSGA-II
(1) NSGA-II简介
NSGA-II,全称为Non-dominated Sorting Genetic Algorithm-II,即非支配排序遗传算法,是一种基于支配的多目标优化算法。从其全称我们可以看出,NSGA-II本质上是一种遗传算法,其选择、交叉、变异算子均与遗传算法相同。那么,NSGA-II相较于普通的GA,有什么不同呢?笔者认为,NSGA-II主要多了两个部分,其一就是其算法名中提到的,非支配排序。其二则是拥挤距离的定义以及基于其的精英保留策略。下面,我们就分开来介绍下这两个部分。
(2) 非支配排序
![[多目标优化算法]1.NSGA-II——非支配排序遗传算法](https://imgs.yssmx.com/Uploads/2023/04/404492-2.png)
非支配排序的原理可以用这幅图来进行解释,如图,对于一整个种群,首先选出当前的Pareto最优解,记为支配等级1;将支配等级1中的解排除后,再从剩余种群中选出Pareto最优解,记为支配等级2;以此类推,直到整个种群被分级完毕。在各支配等级中,每个解和当前等级中的其他任意解均互不支配,支配等级较前(数字较小)的解支配支配等级较后(数字较大)的解。这就是非支配排序。
在实际操作过程中,由于发现最初的非支配排序流程时间复杂度较高,为,其中M为目标数目,N为种群大小。因此,本文提出了一种快速非支配排序方法,将时间复杂度从降为了。其流程如下:
1.对于种群P中的所有个体p,统计支配其的解的个数和其支配的个体的集合。统计结束后,将当前的个体全部加入集合中,并计其支配等级为1。
2.
令(相当于消除支配等级1的解对其的支配,即相当于将支配等级1的个体“移出”当前种群)。
if
(将q加入F2中)
end
end
end
3.对中的个体,计其支配等级为2,并重复2中的操作,以此类推,直到整个种群排序完毕。
(3) 拥挤距离
除了非支配排序外,NSGA-II还定义了拥挤距离的概念,我们同样用图来进行解释:
![[多目标优化算法]1.NSGA-II——非支配排序遗传算法](https://imgs.yssmx.com/Uploads/2023/04/404492-3.png)
如图,对于二目标问题,对于当前的解i(图中黑点i),拥挤距离定义为其相邻解i-1和i+1所形成的四边形的周长,注意,在作图时,这个四边形中不应包含除i外的其他解。由此可见,对于一个解,其拥挤距离越大,这个解周围就越稀疏,选取这样的解,对于保持种群的多样性有益。对于边界解(图中黑点0和l),我们计其拥挤距离为无穷。
(4) NSGA-II流程
有了快速非支配排序和拥挤距离的概念,我们接下来就可以阐述NSGA-II的工作流程.
![[多目标优化算法]1.NSGA-II——非支配排序遗传算法](https://imgs.yssmx.com/Uploads/2023/04/404492-4.png)
如图是NSGA-II的简要流程,首先,对于当前种群,我们使用遗传算法的选择、交叉、变异算子,产生与其个体数目相同的子代,将和合并,记为,并对进行快速非支配排序,注意,此时的个体数目为2N(,各为N)。
非支配排序完后,根据支配等级顺序,依次将各等级个体加入下一种群中,直至当前等级个体不能全部放入为止。如图中,F1、F2个体可以全部放入
,而F3不能全部放入。
此时,对当前等级个体(图中为F3)按照拥挤距离进行排序,并将拥挤距离较大的个体依次加入下一种群中,直到
填满为止(个体数达到N)。此时,将剩余的解全部淘汰。接下来的流程依次类推,直到达到终止条件为止。
通过对NSGA-II流程的阐述,我们可以看到,NSGA-II首先会将支配等级较前的个体加入当前种群,这是算法对收敛性的保证;此外,NSGA-II还会对最后一层个体按照拥挤距离排序,优先选择拥挤距离较大的个体,即边界解和密度较稀疏的个体会被优先保留,这体现了算法对多样性的保证。因此,NSGA-II算法可以同时做到对收敛性和多样性的保证。
(5) NSGA-II的优点与缺点
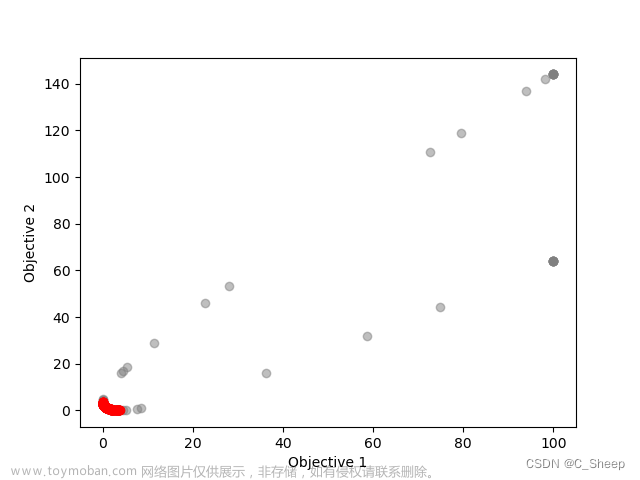
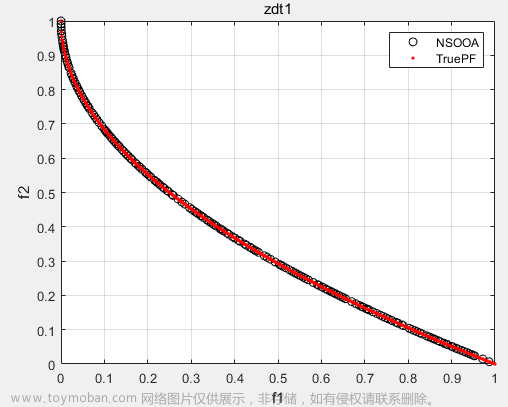
NSGA-II的优点正如上文提到,由于注意对边界解的保留,所以其在解决一些极凸或极凹问题时会较优优势,可以保留较多的边界解。
![[多目标优化算法]1.NSGA-II——非支配排序遗传算法](https://imgs.yssmx.com/Uploads/2023/04/404492-5.png)
如图为NSGA-II对于极凸PF面的处理,可以看到,使用NSGA-II可以保留较多的边界解。
NSGA-II的缺点同样很明显,前文也有提到,NSGA-II是一种基于支配的多目标优化算法。而根据支配的定义,我们可以看到,当多目标优化问题的维度越大时,我们越难找到这种支配关系,甚至可能无法找到,从而使整个种群都互不支配,这样,基于支配的算法就失去了意义。因此,NSGA-II,以及其他基于支配的多目标优化算法,都不适合解决高维多目标优化问题(一般我们认为m>3即为高维问题),或者又称为Many-Objective Problem(MaOP)。
参考文献:
K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, "A fast and elitist multiobjective genetic algorithm: NSGA-II," in IEEE Transactions on Evolutionary Computation, vol. 6, no. 2, pp. 182-197, April 2002, doi: 10.1109/4235.996017.
H. Li, Q. Zhang and J. Deng, "Biased Multiobjective Optimization and Decomposition Algorithm," in IEEE Transactions on Cybernetics, vol. 47, no. 1, pp. 52-66, Jan. 2017, doi: 10.1109/TCYB.2015.2507366.
Wang, Z., Li, Q., Yang, Q. et al. The dilemma between eliminating dominance-resistant solutions and preserving boundary solutions of extremely convex Pareto fronts. Complex Intell. Syst. (2021). https://doi.org/10.1007/s40747-021-00543-2
特别感谢:
遗传算法之NSGA-Ⅱ原理分析和代码解读 - 知乎文章来源:https://www.toymoban.com/news/detail-404492.html
文章来源地址https://www.toymoban.com/news/detail-404492.html
到了这里,关于[多目标优化算法]1.NSGA-II——非支配排序遗传算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!