回溯法解01背包问题（最通俗易懂，附C++代码）-Toy模板网

这篇具有很好参考价值的文章主要介绍了回溯法解01背包问题（最通俗易懂，附C++代码）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

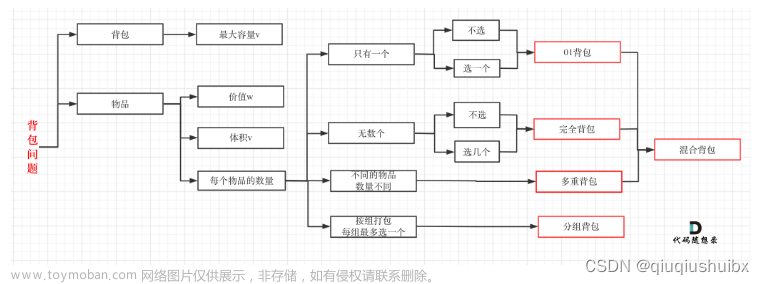
问题描述：

01背包问题是算法中的经典问题，问题描述如下：
对于给定的N个物品，第i个物品的重量为Wi，价值为Vi，对于一个最多能装重量C的背包，应该如何选择放入包中的物品，使得包中物品的总价值最大？

回溯法简介：

回溯法的本质其实就是一种蛮力法，只是通过一定的方法可以使得蛮力法中的一些基本情况可以提前排除从而提高蛮力算法效率，回溯可以理解为排除这些不满足条件的基本情况的过程。

回溯法求解0-1背包问题的过程：

由于直接描述过程比较抽象，因此直接上例题
例题：假设N=3（有三件物品），三个物品的重量为{20，15，10}，三个物品的价值为{20，30，25}，对于一个最大承重为25的背包，求包中物品的组合最大的价值是多少？
题目的参考思路图如下，建议图文对照：（参考书为王红梅老师的《算法设计与分析》）
回溯法解01背包问题（最通俗易懂，附C++代码）
对三件物品分别进行编号1，2，3，初始情况背包是空的
1.首先我们把1号物品放进背包里，此时背包里只有一件物品，总重量为0+20=20，没有超过承重25，因此可以将1号物品成功放入背包内；
2.接下来尝试把2号物品放入背包内，但是发现包中1号物品和2号物品的重量和为20+15=35，超过了承重25，因此不能把2号物品放入背包内；
3.接着考虑3号物品，此时包中只有1号物品。发现1号物品和3号物品的重量和为20+10=30，超过了承重25，因此3号物品也不能放入背包内；
4.由于只有3件物品，并且对于每一种物品我们都考虑过是否将其放入背包内，也就是找到了一种基本情况。找到一个基本情况后，我们就可以看看包里的物品的总价值了。这里包里只有一个1号物品，因此总价值为20；
5.重点来了！回溯过程：每次找出一种满足条件的基本情况就进行一次回溯，找到最后放入包中的物品并将其取出，接着考虑是否放入编号在这个物品之后的第一个物品。这里我们就把1号物品取出，接下来考虑是否放入2号物品；
6.取出1号物品后背包是空的，此时如果放入2号物品，背包总重量为15，没有超过背包承重，因此把2号物品放入背包内；
7.类似地，考虑将3号物品放入背包内。由于2号物品和3号物品的重量和为15+10=25，没有超过承重25，因此将其放入背包内；
8.由于考虑完了3号物品，因此又找到了一个基本情况，记下此时包里物品的总价值，为30+25=55。由于55高于上一种基本情况的总价值，因此将最优解更新为55；
9.进行一次回溯，取出背包中最后放入的物品，也就是3号物品，但是注意：当最后放入背包中的物品恰好是编号最大的物品时，需要额外进行一次回溯。为什么呢？因为编号最大的物品之后已经没有编号更大的物品了，因此没有可以考虑的下一种情况，只能在上一个层面上在进行一次回溯才能产生可能的最优解。（此处不必考虑只放入2号物品的情况，因为一定不是最优解，原因可以自己思考一下）这里再回溯一次，也就是将倒数第二个放入包中的物品取出来，这里就取出2号物品。先后取出3号物品和2号物品之后包应该处于空的状态。
10.上一步中取出了2号物品，因此这一步直接考虑能否放入3号物品，简单的判断后即可得出可以放入，并且同上理也可以得出这是一种基本情况，但是由于包中只有3号物品，总价值为25，没有超过当前的最优解55，因此将该情况忽略。
11.最后一次回溯，取出包中的3号元素。由于此时包已经空了，并且最后一次取出的是编号最大的元素，那么说明算法已经完成了所有情况的遍历，算法终止，55是最优解。文章来源地址https://www.toymoban.com/news/detail-404842.html

程序代码：

#include<iostream>
#include<stack>//由于问题中的包是需要进行后进先出的操作，因此考虑到使用栈这种数据结构（后进先出）
using namespace std;

int maxValue(int w[], int v[], const unsigned& length, const unsigned& capacity)
{
    stack<int> Bag;//首先构造出一个空的背包
    int max = 0;//不同装入情况中背包中物品最大的价值
    int weight = 0;//当前背包中物品的总重量
    int value = 0;//当前背包中物品的总价值
    int i;

    for (i = 0; ; i++)
    {
        if (weight + w[i] <= capacity)//第一种情况：背包装入该物品后不会超重
        {
            Bag.push(i);//将该物品装入背包中
            weight += w[i];//装入物品后背包重量增加
            value += v[i];//装入物品后背包中物品的价值增加
        }
        else//第二种情况：装入该物品后背包超重，则不能将该物品装入包中，相当于什么也不做
        {
            //此处用else语句只是方便理解这是另外一种情况，可以省略
        }

        //当从第一个物品考虑到了最后一个物品时，就确定了一个可以满足条件的装包方法（一个方法就是确定了一个规定每一个物品是否装进包里的策略）
        if (i == length - 1)
        {
            //接下来将本次装包物品价值与当前最高的装包物品价值进行比较，保留较大的一个
            if (max < value)
            {
                max = value;
            }
            //此时取出最后装进包里的一件物品并对其下一件物品进行考虑（这就是算法的重点：回溯的过程！）
            {
                i = Bag.top();//取出上一件装入的东西（这就是回溯的过程）
                Bag.pop();
                weight -= w[i];//取出东西后背包重量减轻
                value -= v[i];//取出物品后背包总价值也会降低
                if (i == length - 1)//特殊情况：如果最后装进包里的物品本来在就是编号最大的物品，那么它后面就没有其他物品了，循环必定终止
                {
                    if (Bag.empty())break;//当所有物品都被从包中拿出来后，这是说明已经遍历完所有情况，查找结束（相当于解空间树中最右边的子树已经走完了）
                    i = Bag.top();//取出上一件装入的东西（这就是回溯的过程）
                    Bag.pop();
                    weight -= w[i];//取出东西后背包重量减轻
                    value -= v[i];//取出物品后背包总价值也会降低
                }
            }
        }
    }
    return max;
}

int main(void)
{
    unsigned num, capacity;
    cout << "请输入物品的个数：";
    cin >> num;
    int* weights = new int[num];
    int* values = new int[num];
    cout << "请输入每件物品的重量：";
    for (unsigned i = 0; i < num; i++)
    {
        cin>>weights[i];
    }
    cout << "请输入每件物品的价值：";
    for (unsigned i = 0; i < num; i++)
    {
        cin >> values[i];
    }
    cout << "请输入包的最大承重：";
    cin >> capacity;
    cout << "该问题的最优解为：" << maxValue(weights, values, num, capacity);
    return 0;
}