目录
1.几种典型的趋近律
1.1等速趋近律
1.2指数趋近律
1.3幂次趋近律
1.4一般趋近律
2.控制器设计
2.1被控对象
2.2选取滑膜面
2.3定义跟踪误差
2.4计算控制律
3.Simulink仿真分析
3.1利用S函数编写被控对象
3.2利用S函数编写控制器
3.3simulink模型
3.4结果分析
1.几种典型的趋近律
1.1等速趋近律

特点:ε表示趋近滑膜面/切换面s = 0的速率;ε越大,则到达切换面越快,但引起的抖动也较大。
1.2指数趋近律

特点:-ks是指数趋近项,k越大,趋近滑模面速度越大;-εsgn(s)是等速趋近项,是为了消除抖振。所以为了保证快速趋近的同时削弱抖振,应增大k的同时减小ε。一般情况该趋近律使用较多。
1.3幂次趋近律

1.4一般趋近律

上述四种趋近律均能保证系统从任意初始状态趋向切换面,即做趋近运动:s-->0;满足滑模到达条件:s*s' ≤ 0。
2.控制器设计
2.1被控对象

2.2选取滑模面

为满足Huiwitz多项式条件,c > 0。
2.3定义跟踪误差

其中:θd(t)为理想位置信号/跟踪信号。
2.4计算控制律
(1)选取指数趋近律:

(2)将误差代入选取的滑模面,并进行求导,有:

(3)联立趋近律,即:

(4)得到控制律/滑模控制器:

3.Simulink仿真分析
取理想信号θd(t) = sint(t),即跟踪该正弦曲线;选取被控对象状态变量为[θ θ’],初始状态为[-0.15 -0.15]
3.1利用S函数编写被控对象
程序如下:
function [sys,x0,str,ts,simStateCompliance] = Plant_2_1(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 2;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 2;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 0;%注无直接馈通关系
sizes.NumSampleTimes = 1; % at least one sample time is needed
sys = simsizes(sizes);
x0 = [-0.15;-0.15];%设定状态变量初值
str = [];
ts = [0 0];
simStateCompliance = 'UnknownSimState';
function sys=mdlDerivatives(t,x,u)
theta = x(1);%θ
dtheta = x(2);%θ'
ddtheta = -25*dtheta+133*u;%θ''
sys = [dtheta;ddtheta];%dx
function sys=mdlUpdate(t,x,u)
sys = [];
function sys=mdlOutputs(t,x,u)
sys = x;
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 1; % Example, set the next hit to be one second later.
sys = t + sampleTime;
function sys=mdlTerminate(t,x,u)
sys = [];3.2利用S函数编写控制器
程序如下:
function [sys,x0,str,ts,simStateCompliance] = Controller_2_1(t,x,u,flag)
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 4;
sizes.NumInputs = 3;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1; % at least one sample time is needed
sys = simsizes(sizes);
x0 = [];
str = [];
ts = [0 0];
simStateCompliance = 'UnknownSimState';
function sys=mdlDerivatives(t,x,u)
sys = [];
function sys=mdlUpdate(t,x,u)
sys = [];
function sys=mdlOutputs(t,x,u)
thetad = u(1);%理想位置信号θd
dthetad = cos(t);%θd'
ddthetad = -sin(t);%θd''
theta = u(2);
dtheta = u(3);
e = thetad-theta;%跟踪误差
de = dthetad-dtheta;
c = 15;
epsilon = 5;k = 10;%调节参数
s = c*e+de;%滑模面
ut = (epsilon*sign(s)+k*s+c*de+ddthetad+25*dtheta)/133;%控制律/滑模控制器
sys = [ut;dthetad;e;de];
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 1; % Example, set the next hit to be one second later.
sys = t + sampleTime;
function sys=mdlTerminate(t,x,u)
sys = [];3.3simulink模型

3.4结果分析

角度θ

角速度θ'

误差e

误差变化率de

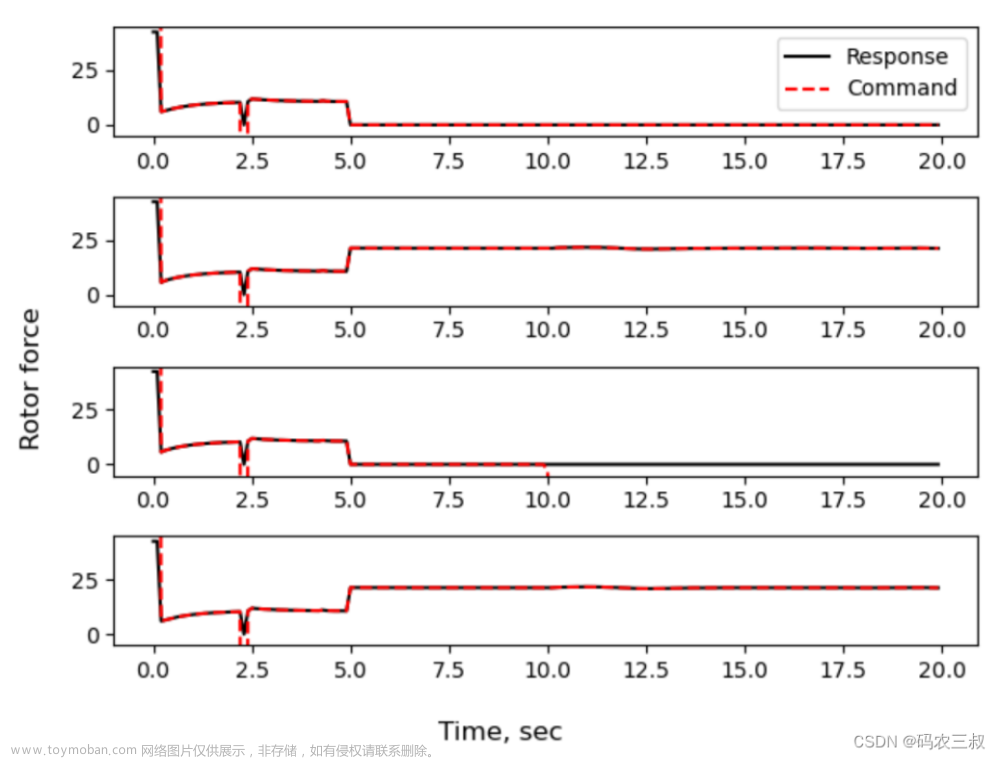
控制输入u
结论:从角位置和角速度可见,该滑膜控制器能实现较好的追踪效果;从误差和误差变化率看,能够通过控制力较快消除误差;但是从控制输入看,出现了很糟糕的抖动,所以后续会提出改进的滑模控制设计。文章来源:https://www.toymoban.com/news/detail-405244.html
注:仅为便利自己学习,错误在所难免,如有侵权,请联系删除,有兴趣的学者可以参考学习交流,谢谢!文章来源地址https://www.toymoban.com/news/detail-405244.html
到了这里,关于VSC/SMC(一)——基于趋近律的滑模控制(含程序模型)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!