【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

Halo，这里是Ppeua。平时主要更新C语言，C++，数据结构算法......感兴趣就关注我吧！你定不会失望。

🌈个人主页：主页链接

🌈算法专栏：专栏链接

我会一直往里填充内容哒！

🌈LeetCode专栏：专栏链接

目前在刷初级算法的LeetBook 。若每日一题当中有力所能及的题目，也会当天做完发出

🌈代码仓库：Gitee链接

🌈点击关注=收获更多优质内容🌈

0.二叉树的链式结构实现

先来看看BuyNode():

1.前序遍历:

1.1前序遍历代码实现

1.2深度优先搜索

2.中序遍历:

2.1中序遍历代码实现

3.后序遍历:

3.1后序遍历代码实现

4.前中后遍历的差别及互相转换

4.1前中推树的结构

4.2中后推树的结构

4.3前后推树的结构

完结撒花：

【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

0.二叉树的链式结构实现

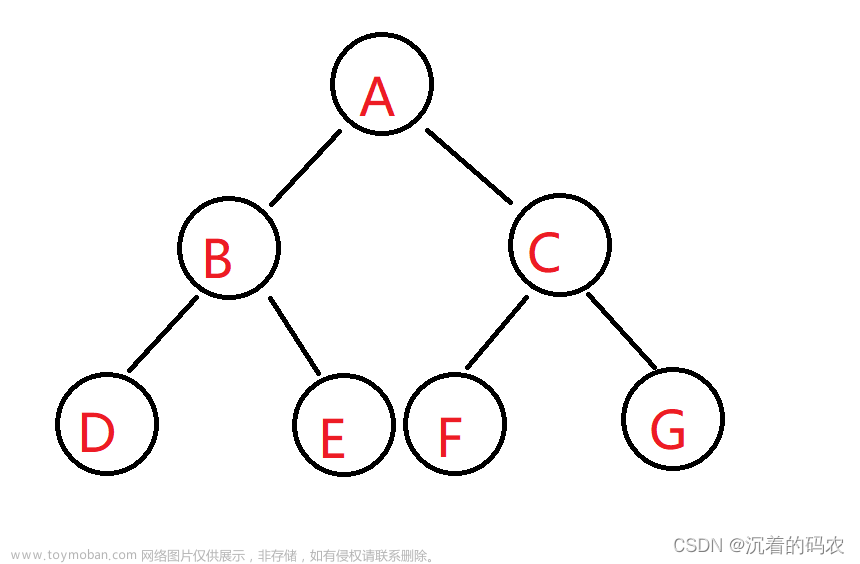
上文提到过，在简单二叉树当中，我们一般采用双指针链式结构存储的方式，其结构长这样

【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

其结构体中包含三个值 left,right,val三个值

struct tree{
    int val;
    tree* left;
    tree* right;
};

为了方便之后遍历的调试,我们先初始化下这颗二叉树

先来看看BuyNode():

与之前链表的Node类似,所以就不细讲了(给定一个值,malloc其节点,将值存入x,其左右指针置空,返回这个节点值)

tree* BuyNode(TDataType x)
{
	tree* tmp = (tree*)malloc(sizeof(tree));
	tmp->x = x;
	tmp->left = NULL;
	tmp->right = NULL;
	return tmp;
}

之后将每个节点连接起来.

tree* CreateTree()
{
	tree* node1 = BuyNode(1);
	tree* node2 = BuyNode(2);
	tree* node3 = BuyNode(3);
	tree* node4 = BuyNode(4);
	tree* node5 = BuyNode(5);
	tree* node6 = BuyNode(6);
	tree* node7 = BuyNode(7);
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	return node1;
}

连接图就长这样. 【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

初始化完二叉树,就开始进入正题吧!

1.前序遍历:

树是一个递归的过程,所以进行遍历的时候,往往采用递归的方法比较简单(代码上),思维上当你理解了递归,也会发现就不过如此.

我们先来了解下前序遍历的含义:前序遍历顾名思义就是从根开始遍历,其遍历顺序为先访问根再访问其左节点,之后才是右节点,对于每一颗子树都是如此.

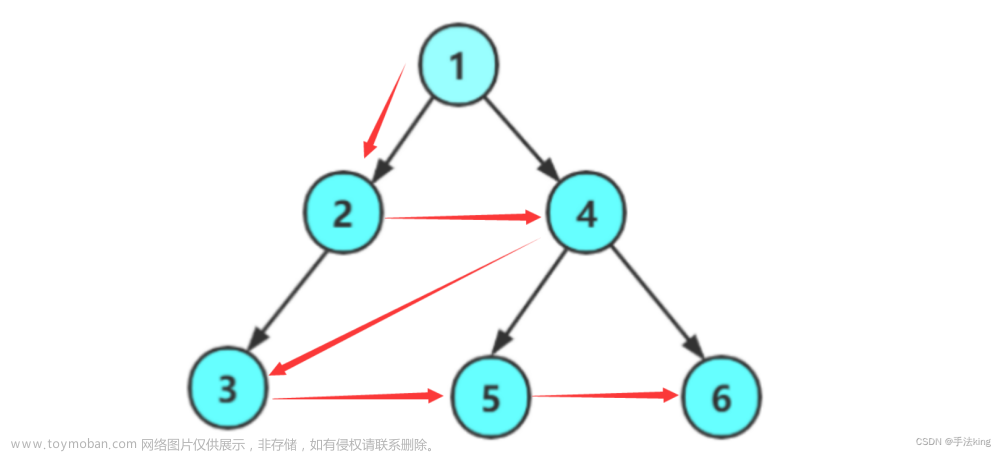
例如这幅图,其先遍历根(1) 在遍历其左子树

进入左子树时,先访问其根(2) 在遍历其左子树

进入左子树时,先访问其根(3) 在遍历其左子树发现为空!再遍历右子树,发现也为空,则返回到上一层(2)

此时再遍历根为(2)的右子树发现为空,则返回到上一层(1)

此时在遍历其右子树

先访问其根(4)在遍历其左子树

进入左子树时,先访问其根(5) 在遍历其左子树发现为空!再遍历右子树,发现也为空,则返回到上一层(4)

此时再访问根为(4)的右子树其根为(6) 左右子树都为空则返回.

返回到根为1的节点就结束了

直接看文字似乎十分的绕,下面可以看看这幅图 【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

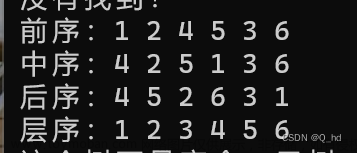
所以前序遍历结果为:1 2 3 4 5 6,第一个为该树的根

1.1前序遍历代码实现

void Preorder(tree* tr)
{
	if (tr == NULL)
	{
		printf("NULL  ");
		return;
	}
	printf("%d  ", tr->x);
	Preorder(tr->left);
	Preorder(tr->right);
}

这是模板,遇到节点直接打印,空的话就返回到上一层当中.虽然这代码十分的简短,但第一次遇到的时候,其背后的思考量还是很大的.

以下为递归展开图,推荐自己动手画一下.

【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

1.2深度优先搜索

这与深度优先搜索十分的相似

2.中序遍历:

中序遍历相较于前序改变的只是遍历根的顺序,前序为:根左右根在前

所以中序遍历为:左根右先遍历完左子树,在访问其根节点,再遍历其右子树

【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

其遍历完的结果为:321546

其遍历顺序是这样的. 可以看出他会先走到最左边的节点访问(因为没有左右节点了),之后访问此左节点的根节点,之后是右节点

又因为这个根节点又有其父节点,所以以此类推.

【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

2.1中序遍历代码实现

void Inorder(tree* tr)
{
	if (tr == NULL)
	{
		printf("NULL  ");
		return;
	}
	Inorder(tr->left);
	printf("%d  ", tr->x);
	Inorder(tr->right);
}

3.后序遍历:

依旧如之前所说,改变的只是访问根的时机,所以后序遍历的方式为:左右根

也就是先访问左节点再访问右节点,最后才访问根节点

【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

按照这个顺序遍历下来,其结果为:325641 可以看到根在最后

3.1后序遍历代码实现

void Postorder(tree* tr)
{
	if (tr == NULL)
	{
		printf("NULL  ");
		return;
	}
	Postorder(tr->left);
	Postorder(tr->right);
	printf("%d  ", tr->x);
	
}

4.前中后遍历的差别及互相转换

前序遍历根在前

中序遍历根在中间

后序遍历根在最后

我们可以通过根据任意前/后+中序遍历的结果,推导出这棵树的结构

4.1前中推树的结构

【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

刚刚提到前序遍历的根在第一个,而中序遍历的根在中间,

找到其所在位置,理出其左右子树

所以这颗二叉树应该是长这样的

【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

之后再依据刚刚的规律,通过前序的结果发现47当中 7是根 9621当中 9是根

【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

又通过中序的结果发现6是9的左子树的根 12是9的右子树通过前序看出 2是根 1是左子树

所以这颗树就被画出来了

【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

可以发现 找根用前序遍历,找左右子树用中序遍历的结果

4.2中后推树的结构

中序结果为:4756912 后序结果为 4761295

依然先通过后续遍历的最后一个结果确定整棵树的根为5 然后依据中序的结果分出左右子树

为 47 5 6912

之后再次通过刚刚的方法与前序遍历大同小异这里就不赘述了.

找根用后序遍历,找左右子树用中序遍历的结果

4.3前后推树的结构

这样是推不出来的 ,当这颗树只有两个节点的时候,无法分辨其为左子树还是右子树

【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式

也可以得出:若前序后序刚好相反 ,其只有一个叶子节点

完结撒花：

🌈本篇博客的内容【前中后层序遍历 --二叉树的结构特点与遍历方式】已经结束。

🌈若对你有些许帮助，可以点赞、关注、评论支持下博主，你的支持将是我前进路上最大的动力。

🌈若以上内容有任何问题，欢迎在评论区指出。若对以上内容有任何不解，都可私信评论询问。

🌈诸君，山顶见！文章来源地址https://www.toymoban.com/news/detail-405806.html

到了这里，关于【数据结构】前中后层序遍历 --二叉树的结构特点与遍历方式的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！