C语言实现求解斐波那契数列的四种方法及优化处理（递归，迭代，特殊性质公式，矩阵快速幂）-Toy模板网

这篇具有很好参考价值的文章主要介绍了C语言实现求解斐波那契数列的四种方法及优化处理（递归，迭代，特殊性质公式，矩阵快速幂）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

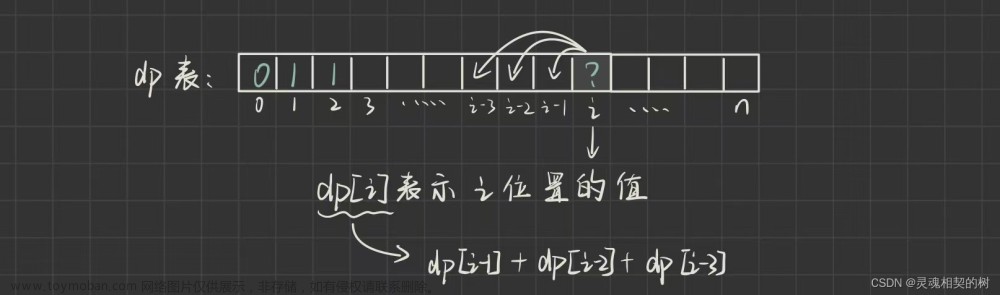
众所周知，斐波那契数列是非常经典的一个数列，它的数学公式如下 C语言实现求解斐波那契数列的四种方法及优化处理（递归，迭代，特殊性质公式，矩阵快速幂）

为了便于观察，我们列出它的几项：0 1 1 2 3 5 8 13 21......

下面我们将介绍四种方法来用C语言计算机代码实现对斐波那契数列的求解，分别是：递归法，迭代法，矩阵求解法以及特殊性质公式。

一、递归法

（PS：没有递归基础的建议先学习递归的基础概念，在此我仅简要介绍一下递归的思想和求解代码）

在递归的实现中，我们知道，递归有两个要求：（1）进行递归这一操作所需要满足的条件（2）此条件需要最终不被满足，使得函数的嵌套调用能够返回。在斐波那契数列中，我们知道当x=0时，返回值为0；当x=1时，返回值为1。所以，要求（1）中所需要满足的条件即x>=2；而要求（2）中要使该条件最终不被满足，即x不断减小，且最终为0或1。

于是我们给出代码的实现：

int Fibonacci(int x)
{
    if (x >= 2)
        return Fibonacci(x - 1) + Fibonacci(x - 2);    //当x>=2时，继续按照公式f（x）=f（x-1）+f（x-2）嵌套调用
    else if (x == 1)
        return 1;    //当x=1时，返回1，同时嵌套调用开始返回
    else
        return 0;    //当x=0时，返回0，同时嵌套调用开始返回
}

用递归的方法求解斐波那契数列是不是非常简单呢？ C语言实现求解斐波那契数列的四种方法及优化处理（递归，迭代，特殊性质公式，矩阵快速幂）

然而！用递归的方法也有一个很大的缺点：栈溢出！

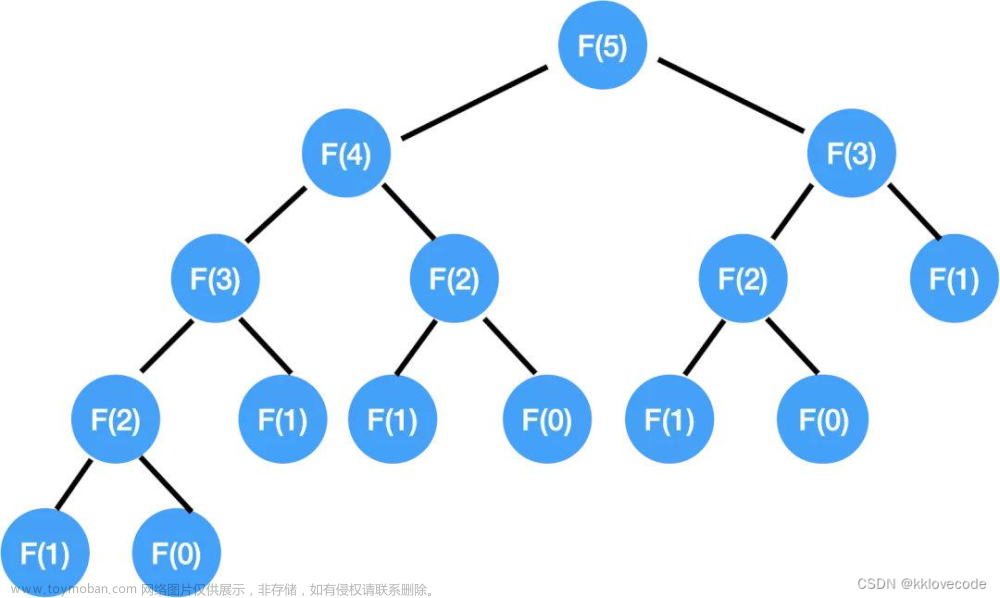
栈：函数及其形参的空间由栈分配，在函数调用未完成时，为其分配的空间并不会销毁！于是当递归中函数的调用次数过多时，会导致栈溢出的问题。在本题的递归中，我们能发现，当我们求

F（5）= F（4）+F（3）

= F（3）+F（2）+F（2）+F（1）

= F（2）+F（1）+F（1）+F（0）+F（1）+F（0）+F（1）时，不仅对F（2）进行了多次调用，甚至还进行了多次计算！这就导致计算效率的大幅降低以及资源占用的大幅增加。

于是我们给出第二种方法。

二、迭代法

什么是迭代法？ C语言实现求解斐波那契数列的四种方法及优化处理（递归，迭代，特殊性质公式，矩阵快速幂）

迭代法也称辗转法，是一种不断用变量的旧值递推新值的过程。

也就是说，这是一种各个变量直接相互作用的过程。

分析思路：设有a、b、c三个变量，以及我们输入的第x项的x，令a=0（第一个斐波那契数）b=1（第二个斐波那契数），当x>=2时，c=a+b，同时再令a、b分别往右移一个数，如此往复x-2次，c的值就变成了第x个数的值。

下面给出代码：

int Fibonacci(int x)
{
    int a = 0;
    int b = 1;
    int c = 0;
    if (x == 1)
        return 1;    //当x=1，返回1
    if (x == 0)
        return 0;    //当x=0，返回0
    while (x >= 2)   //输入x>=2时，进行迭代
    {
        c = a + b;   //每次迭代令c=a+b，即进行f（x）=f（x-1）+f（x-2）
        a = b;       //使得a，b往后移一个数字
        b = c;
        x--;
    }
    return c;
}

三、特殊性质公式法

同递归法，只不过需要用到公式：

F（n+m）=F（m）F（n+1）+F（m-1）F（n）

在这个公式下，F（x）可以转换为F（（x/2） + x-（x/2）），即一种二分思想，可以将时间复杂度为O（n）的算法转化为时间复杂度为O（log n）的算法。

下面给出代码：

int Fibonacci(int x)
{
    if (x == 1 || x == 2)    //当x=2时也要返回1，否则将进入死循环。
        return 1;
    if (x == 0)
        return 0;
    int a = x / 2;
    int b = x - a;
    return Fibonacci(a + 1) * Fibonacci(b) + Fibonacci(a) * Fibonacci(b - 1);
}

C语言实现求解斐波那契数列的四种方法及优化处理（递归，迭代，特殊性质公式，矩阵快速幂）

然而虽然但是事实上这个方法还是不如迭代法来得实在的QoQ

四、矩阵法

C语言实现求解斐波那契数列的四种方法及优化处理（递归，迭代，特殊性质公式，矩阵快速幂）

于是，只要先算出系数矩阵的n-1次幂，再用与之相乘即可求出F（n）

下面是用矩阵快速幂的方法求出所需矩阵n-1次幂的代码：

(PS：小编只学了快速幂，这个矩阵快速幂的算法是自己琢磨出来的，可能不标准，如果有心可以去学一下矩阵快速幂的算法！！下面会给出一般快速幂的算法给各位小可爱们参考一下~)

int Fibonacci(int x)
{
    if (x == 0)
        return 0;
    if (x == 1 || x == 2)
        return 1;
    int a[2][2] = { {1,1},{1,0} };
    int b[2][2] = { {1,1},{1,0} };
    int c[2][2] = { {1,0},{0,1} };
    int d[2][2] = { {1,0},{0,1} };
    int t = x - 1;
    while (t)
    {
        if (t%2==1)
        {
            d[0][0] = c[0][0] * b[0][0] + c[0][1] * b[1][0];
            d[0][1] = c[0][0] * b[0][1] + c[0][1] * b[1][1];
            d[1][0] = c[1][0] * b[0][0] + c[1][1] * b[1][0];
            d[1][1] = c[1][0] * b[0][1] + c[1][1] * b[1][1];
            c[0][0] = d[0][0];
            c[0][1] = d[0][1];
            c[1][0] = d[1][0];
            c[1][1] = d[1][1];
        }
        b[0][0] = a[0][0] * a[0][0] + a[0][1] * a[1][0];
        b[0][1] = a[0][0] * a[0][1] + a[0][1] * a[1][1];
        b[1][0] = a[1][0] * a[0][0] + a[1][1] * a[1][0];
        b[1][1] = a[1][0] * a[0][1] + a[1][1] * a[1][1];  
        a[0][0] = b[0][0];
        a[0][1] = b[0][1];
        a[1][0] = b[1][0];
        a[1][1] = b[1][1];
        t >>= 1;
    }
    return c[0][0];
}

其中F（x） = c[0][0]F（1）+c[1][0]F（0） = c[0][0]

快速幂代码：

int f(int a,int n)
{
    int ans = 1;
    while (n)
    {
        if (n & 1 == 1)    //判断n的最后一位是否为1
        {
            ans *= a;
        }
        a *= a;            //a每次自乘a，使得a在每次循环中分别为a，a^2,a^3...
        n >>= 1;           //n右移一，使得n的二进制表示中1所在的位置所代表的位全与a当前的次幂相同
    }
    return ans;
}