一、前言
BP神经网络预测回归MATLAB代码(代码完整可用,复制后即可运行使用,操作简单)
(1)BP神经网络的知识想必不用再过多介绍,本篇文章从实际应用的角度,针对新手应用者,针对不需要过多了解BP,但是需使用MATLAB进行BP预测使用的童鞋们(就是那些我不需要懂,能用就行的童鞋们),展示了一套完整且注释详细的BP神经网络MATLAB代码,供各位直接使用。
(2)此代码展示了丰富的结果表现形式,包含了常用的各种结果指标,包括误差平方和SSE、平均绝对误差MAE、均方误差MSE、均方根误差RMSE、平均百分比误差MAPE、预测准确率、相关系数R。此外,本代码还包含了隐含层节点的寻优过程,自动计算出最佳隐含层节点,避免了随意设置导致的误差增大和反复的实验过程。
(3)代码共分为9部分,分别为:初始化、读取数据、设置训练集和测试集、数据归一化、求解最佳隐含层、构建最佳隐含层的BP神经网络、网络训练、网络测试、结果输出。
代码获取:直接点击链接
二、代码部分
2.1 初始化
%% 1.初始化
clear
close all
clc
format short %精确到小数点后4位,format long是精确到小数点后15位
2.2 读取数据
(1)此部分采用xlsread函数读取Excel中存储的数据集,xlsread(‘数据.xlsx’,‘Sheet1’,‘A1:N520’)中的’数据.xlsx’代表Excel文件名称,'Sheet1’代表文件的第一个表格,'A1:N520’代表数据矩阵,即包括输入和输出全部的数据范围,使用需自行修改;
(2)testNum代表设置测试集样本的数量,根据自己需求设置,剩下的为训练集;
(3)新版本的MATLAB(好像是2021版本以上)无法使用xlsread函数,可用Load函数替代 ,Load函数用法可直接百度,很简单。
%% 2.读取数据
data=xlsread('数据.xlsx','Sheet1','A1:N520'); % Matlab2021版本以上无法使用xlsread函数,可用Load函数替代
% 设置神经网络的输入和输出
input=data(:,1:end-1); %第1列至倒数第2列为输入
output=data(:,end); %最后1列为输出
N=length(output); %计算样本数量
testNum=20 ; %设定测试集样本数量,从数据集后面选取
trainNum=N-testNum; %设定训练集样本数量
2.3 设置训练集和测试集
%% 3.设置训练集和测试集
input_train = input(1:trainNum,:)'; % 训练集输入
output_train =output(1:trainNum)'; % 训练集输出
input_test =input(trainNum+1:trainNum+testNum,:)'; % 测试集输入
output_test =output(trainNum+1:trainNum+testNum)'; % 测试集输出
2.4 数据归一化
%% 4.数据归一化
[inputn,inputps]=mapminmax(input_train,0,1); % 训练集输入归一化到[0,1]之间
[outputn,outputps]=mapminmax(output_train); % 训练集输出归一化到默认区间[-1, 1]
inputn_test=mapminmax('apply',input_test,inputps); % 测试集输入采用和训练集输入相同的归一化方式
2.5 求解最佳隐含层
(1)计算出输入和输出矩阵的列数,即为输入节点数和输出节点数;
(2)根据输入节点数和输出节点数计算隐含层节点的范围。隐含层节点的范围由公式(1)计算得出,m代表输入层节点数,n代表输出层节点数,a的取值范围为1~10之间的整数,根据公式(1)求出10个可选择的隐含层节点数,依次对BP网络设置这10个隐含层节点并通过计算训练集均方误差MSE的方式,最终得出误差最小所对应的隐含层节点,即为最佳隐含层节点。

%% 5.求解最佳隐含层
inputnum=size(input,2); %size用来求取矩阵的行数和列数,1代表行数,2代表列数
outputnum=size(output,2);
disp(['输入层节点数:',num2str(inputnum),', 输出层节点数:',num2str(outputnum)])
disp(['隐含层节点数范围为 ',num2str(fix(sqrt(inputnum+outputnum))+1),' 至 ',num2str(fix(sqrt(inputnum+outputnum))+10)])
disp(' ')
disp('最佳隐含层节点的确定...')
%根据hiddennum=sqrt(m+n)+a,m为输入层节点数,n为输出层节点数,a取值[1,10]之间的整数
MSE=1e+5; %误差初始化
transform_func={'tansig','purelin'}; %激活函数采用tan-sigmoid和purelin
train_func='trainlm'; %训练算法
for hiddennum=fix(sqrt(inputnum+outputnum))+1:fix(sqrt(inputnum+outputnum))+10
net=newff(inputn,outputn,hiddennum,transform_func,train_func); %构建BP网络
% 设置网络参数
net.trainParam.epochs=1000; % 设置训练次数
net.trainParam.lr=0.01; % 设置学习速率
net.trainParam.goal=0.000001; % 设置训练目标最小误差
% 进行网络训练
net=train(net,inputn,outputn);
an0=sim(net,inputn); %仿真结果
mse0=mse(outputn,an0); %仿真的均方误差
disp(['当隐含层节点数为',num2str(hiddennum),'时,训练集均方误差为:',num2str(mse0)])
%不断更新最佳隐含层节点
if mse0<MSE
MSE=mse0;
hiddennum_best=hiddennum;
end
end
disp(['最佳隐含层节点数为:',num2str(hiddennum_best),',均方误差为:',num2str(MSE)])
2.6 构建最佳隐含层的BP神经网络
(1)根据2.5求出来的最佳隐含层节点,重新构建最佳隐含层的BP神经网络;
(2)网络参数可根据自己需求适当修改。
%% 6.构建最佳隐含层的BP神经网络
net=newff(inputn,outputn,hiddennum_best,transform_func,train_func);
% 网络参数
net.trainParam.epochs=1000; % 训练次数
net.trainParam.lr=0.01; % 学习速率
net.trainParam.goal=0.000001; % 训练目标最小误差
2.7 网络训练
%% 7.网络训练
net=train(net,inputn,outputn); % train函数用于训练神经网络,调用蓝色仿真界面
2.8 网络测试
(1)运行完毕后可查看工作区中最终的权值阈值。
%% 8.网络测试
an=sim(net,inputn_test); % 训练完成的模型进行仿真测试
test_simu=mapminmax('reverse',an,outputps); % 测试结果反归一化
error=test_simu-output_test; % 测试值和真实值的误差
% 权值阈值
W1 = net.iw{1, 1}; %输入层到中间层的权值
B1 = net.b{1}; %中间各层神经元阈值
W2 = net.lw{2,1}; %中间层到输出层的权值
B2 = net.b{2}; %输出层各神经元阈值
2.9 结果输出
(1)本部分为结果的输出代码,包括预测值与实际值对比图、预测误差图、计算各项参数指标、显示结果。
%% 9.结果输出
% BP预测值和实际值的对比图
figure
plot(output_test,'bo-','linewidth',1.5)
hold on
plot(test_simu,'rs-','linewidth',1.5)
legend('实际值','预测值')
xlabel('测试样本'),ylabel('指标值')
title('BP预测值和实际值的对比')
set(gca,'fontsize',12)
% BP测试集的预测误差图
figure
plot(error,'bo-','linewidth',1.5)
xlabel('测试样本'),ylabel('预测误差')
title('BP神经网络测试集的预测误差')
set(gca,'fontsize',12)
%计算各项误差参数
[~,len]=size(output_test); % len获取测试样本个数,数值等于testNum,用于求各指标平均值
SSE1=sum(error.^2); % 误差平方和
MAE1=sum(abs(error))/len; % 平均绝对误差
MSE1=error*error'/len; % 均方误差
RMSE1=MSE1^(1/2); % 均方根误差
MAPE1=mean(abs(error./output_test)); % 平均百分比误差
r=corrcoef(output_test,test_simu); % corrcoef计算相关系数矩阵,包括自相关和互相关系数
R1=r(1,2);
% 显示各指标结果
disp(' ')
disp('各项误差指标结果:')
disp(['误差平方和SSE:',num2str(SSE1)])
disp(['平均绝对误差MAE:',num2str(MAE1)])
disp(['均方误差MSE:',num2str(MSE1)])
disp(['均方根误差RMSE:',num2str(RMSE1)])
disp(['平均百分比误差MAPE:',num2str(MAPE1*100),'%'])
disp(['预测准确率为:',num2str(100-MAPE1*100),'%'])
disp(['相关系数R: ',num2str(R1)])
%显示测试集结果
disp(' ')
disp('测试集结果:')
disp(' 编号 实际值 BP预测值 误差')
for i=1:len
disp([i,output_test(i),test_simu(i),error(i)]) % 显示顺序: 样本编号,实际值,预测值,误差
end
三、输出结果展示
(1)最佳隐含层节点的确定过程:

(2)各项误差指标结果

(3)打印测试集结果

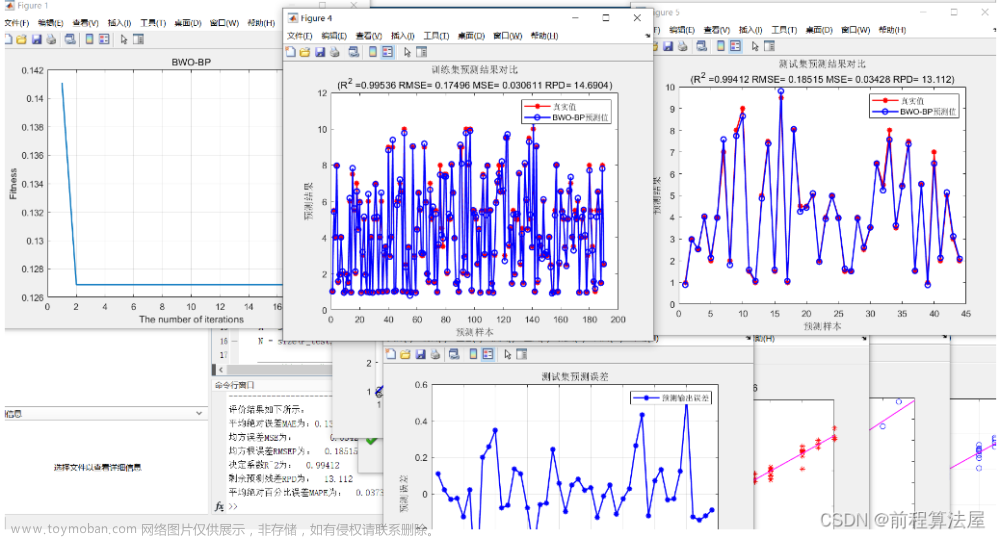
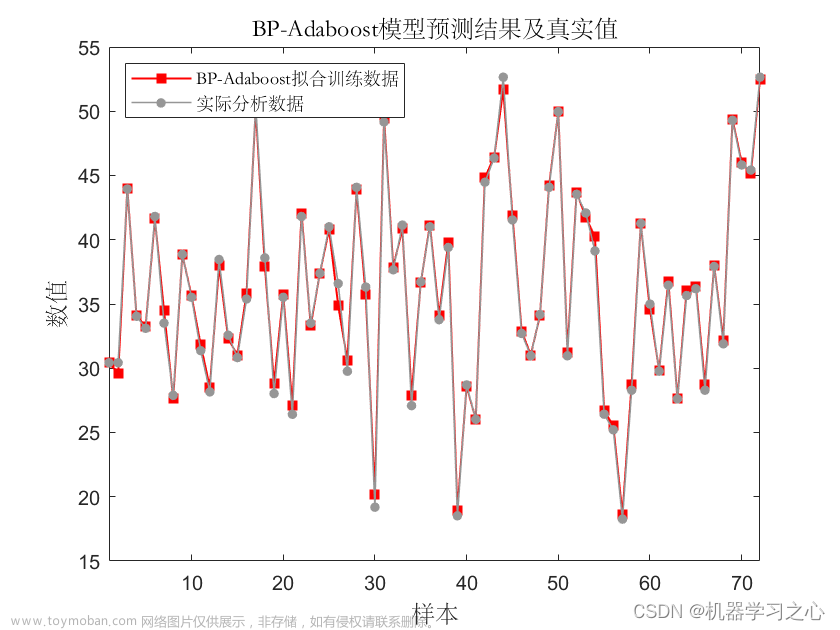
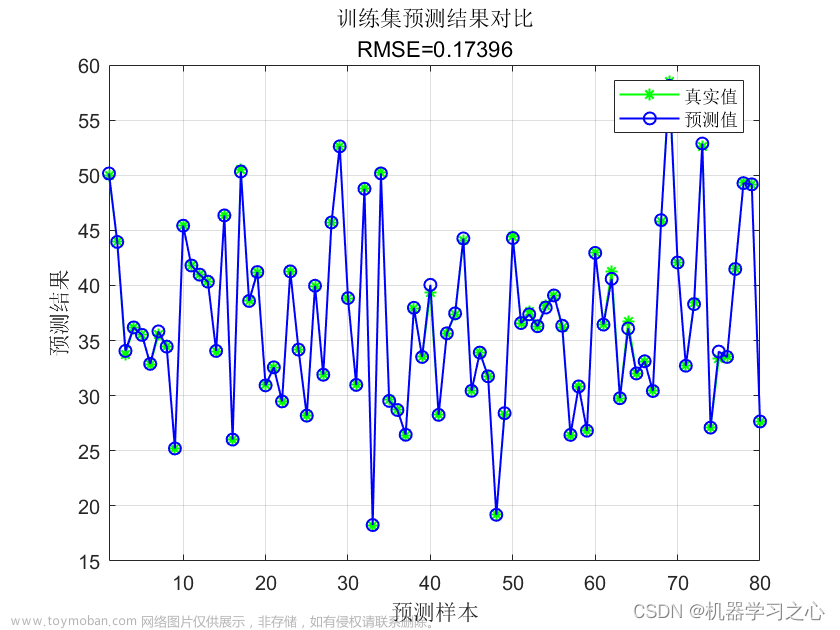
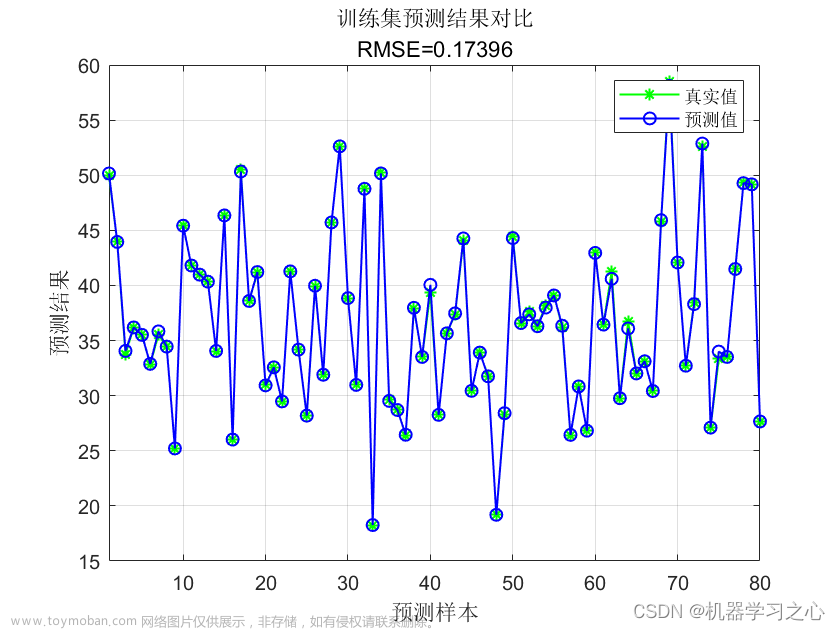
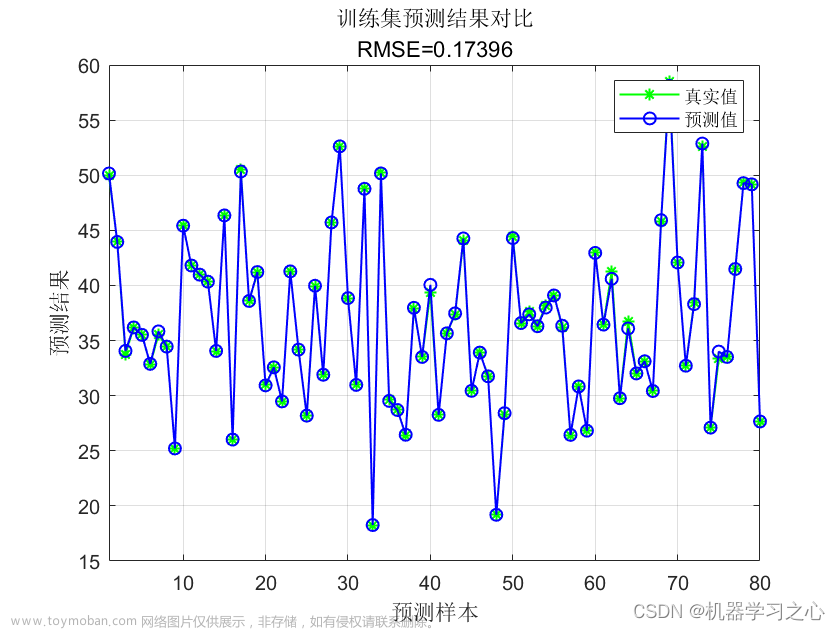
(4)BP预测值和实际值的对比以及预测误差

(5)回归图和误差直方图

(6)其他训练结果
 文章来源:https://www.toymoban.com/news/detail-406573.html
文章来源:https://www.toymoban.com/news/detail-406573.html
四、BP优化模型
| BP | |
|---|---|
| 布谷鸟算法优化 CS-BP | |
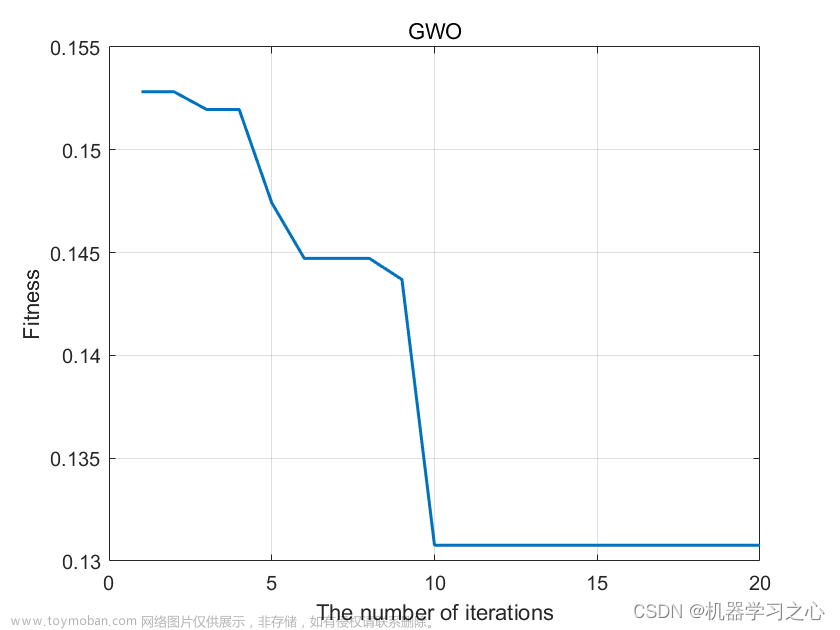
| 灰狼算法优化 GWO-BP | |
| 鲸鱼算法优化 WOA-BP | |
| 粒子群算法优化 PSO-BP | |
| 麻雀算法 SSA-BP | |
| 遗传算法 GA-BP |
五、结语
(1)本代码可以算作是BP神经网络预测的较为优质的代码,大部分的设置是自动计算,无需手动修改,替换数据集后可直接使用,不懂得小伙伴根据文章也可直接使用,非常便捷;
(2)本代码为多输出单输出神经网络,后续会发布多输出多输出的BP代码,敬请期待。文章来源地址https://www.toymoban.com/news/detail-406573.html
到了这里,关于BP神经网络预测回归MATLAB代码(代码完整可直接用,注释详细,可供学习)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!