【数据处理方法】主成分分析（PCA）原理分析-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据处理方法】主成分分析（PCA）原理分析。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

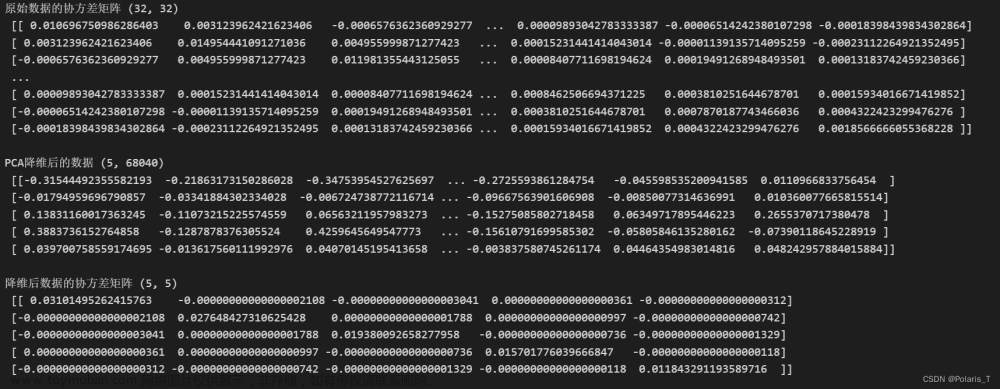
笔者最近在学习的过程需要使用一些数据分析和处理的方法，而PCA就是其中常用的一种手段。但在自学的过程中，由于笔者水平有限，对一些博客中的公式不是能很好理解（数学不好的辛酸Ծ‸Ծ），导致总是对整个方法的原理没有一个透彻的理解。后来在视频用最直观的方式告诉你：什么是主成分分析PCA_哔哩哔哩_bilibili

的帮助下，笔者终于从整体上理解了该方法，在此也向该视频作者致以诚挚的感谢。接下来，笔者尽量用自己的话来总结从该视频中的收获，谈谈对PCA原理的理解。为照顾一些和笔者一样基础不太好的小伙伴，这里尽量使用少的公式，而用一些图示来辅助理解。如无特别标明，本文所用的所有图片均来自上述视频。

事先说明，如果仅是对PCA步骤感兴趣的小伙伴，可以直接跳到总结部分，也方便节约时间。：）

一.PCA简介

主成分分析（Principal components analysis, PCA），顾名思义，其目的在于提取数据中的主要成分信息，因此，常用于对数据的提炼，例如：降维（使用最多的领域之一），异常值检测等，是数据分析中的一种重要方法。

那么，PCA究竟做了什么呢？我们通过下面的图来简单理解一下：

【数据处理方法】主成分分析（PCA）原理分析

我们首先来看一个特殊情况，假如在原坐标系下，有这样六个点，每个点的坐标包括x和y，这样，当我们要记录这些点的坐标时，我们需要同时记录它们的x坐标和y坐标，也就是要记录2个维度的信息。

那么，假如我们移动坐标系，让新坐标系如右所示，令所有的点都位于一个轴上，同时能较好的保留原先数据分布的信息。这样，由于在y'上坐标全部为0，因此我们完全可以去掉，仅用x'坐标就可以表示这些点。这样，原先需要保存2维的坐标信息，在进行这样的坐标系转换后，就仅需保留1维的坐标信息，我们便完成了对数据的提炼，或者在这里，可以称为对数据的降维。

相信在看了上面一段话后，有的小伙伴已经悟到了，没错，PCA所作的，就是这样一个坐标系转换的事情。

【数据处理方法】主成分分析（PCA）原理分析

PCA其实目的就是为了寻找这样一个转换后的坐标系，使数据能尽可能分布在一个或几个坐标轴上，同时尽可能保留原先数据分布的主要信息，使的原先高维度的信息，在经过转换后可以用低维度的信息来保存。而新坐标系的坐标轴，称为主成分(Principal components, PC), 这也就是PCA的名称来源。

那么，怎么样的坐标系，算是“保留信息最多呢”？

【数据处理方法】主成分分析（PCA）原理分析

答：选择数据分布最分散，即方差最大的方向。

可以对比上面两张图上的两个坐标轴方向，可以看到，当数据投影到图一方向的坐标轴上时，数据分布的最为分散，此时，方差也是最大，这种情况下，能够最完整的保留原先数据的差异性，从而便于区分。

而在图二中，数据在坐标轴上的投影就有许多重叠的地方，方差会较小，这种情况下，原先差异性很大的数据在投影后便无法区分，没有保留原先数据的信息，不是一个好的方向。

因此，我们把方差最大的方向选为主成分1的方向，其垂直方向即为主成分2方向，以此类推。

二.PCA方法

在了解PCA的目的后，接下来，就是考虑如何实现，即如何实现这样的坐标系转换。

1. 去中心化

首先，要将数据去中心化，即将坐标原点放在数据中心。若不执行去中心化，就会出现这种现象：

【数据处理方法】主成分分析（PCA）原理分析

相当于在原地空转，可能发现不了最好的方向。

进行了去中心化后，将数据中心放在坐标原点，则就会避免这个问题。

【数据处理方法】主成分分析（PCA）原理分析

2. 找坐标系

即找到方差最大的方向。

在回答这个问题前，我们首先回顾一下矩阵线性变换的知识。

1) 拉伸

【数据处理方法】主成分分析（PCA）原理分析

拉伸矩阵S的特点是只在对角线上有数字，即拉伸矩阵是对称矩阵，满足,它实现的数据在轴上的水平拉伸（包括缩放）。

2)旋转

【数据处理方法】主成分分析（PCA）原理分析

如图，旋转矩阵的特点是，其逆矩阵就等于其本身，即，图中R的操作，实现的是逆时针旋转坐标轴θ角。

【数据处理方法】主成分分析（PCA）原理分析

我们手里的数据，其实就相当于一个服从多维高斯分布的数据经过拉伸和旋转之后形成的数据，因此，找到方差最大的方向，其实就是求这个旋转矩阵R，即求我们旋转的角度。

如何求R，这里先给个结论，协方差矩阵的特征向量就是R。具体推导我们慢慢来：

【数据处理方法】主成分分析（PCA）原理分析

首先回顾一下协方差的概念，协方差代表的是两个变量变化的一个相关程度，如果x增大，y也增大，则成为正相关；反之，则为负相关，而这个相关的程度，就是协方差。x和y的协方差用cov（x,y）表示，正相关时，cov(x,y)>0;负相关时，cov(x,y)<0,不相关则为0。顺便一提，变量自己和自己的协方差，就是方差，即cov(x,x)=var(x)

因此，协方差矩阵的表示如下：

【数据处理方法】主成分分析（PCA）原理分析当数据进行拉伸和旋转时，协方差也会随之改变，根据协方差的定义，协方差矩阵也可以通过这样计算得到。