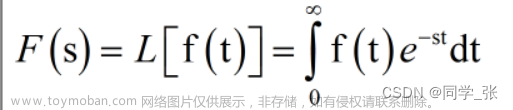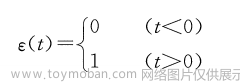图谱论学习—拉普拉斯矩阵背后的含义-Toy模板网

这篇具有很好参考价值的文章主要介绍了图谱论学习—拉普拉斯矩阵背后的含义。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、为什么学习拉普拉斯矩阵

早期，很多图神经网络的概念是基于图信号分析或图扩散的，而这些都需要与图谱论相关的知识。并且在图网络深度学习中（graph deep learning）中，拉普拉斯矩阵是很常用的概念，深入理解其物理含义非常有助于加深对GNN模型的理解。博主最近在学习GCN，想要在拉普拉斯矩阵方面有个更加深入的了解，看了不少文献资料与网上的解读，受益匪浅。
图谱论学习—拉普拉斯矩阵背后的含义

二、拉普拉斯矩阵的定义与性质

    对于一个有n个顶点的图G，它的拉普拉斯矩阵(Laplacian Matrix)定义为： $L = D - A$     其中，D是图G的度矩阵，A是图G的邻接矩阵。L中的元素可定义为：
$L_{ij}= \begin{cases} d(v_i)& 如果i=j \\ -A_{ij}& 如果i\ {\neq}\ j并且v_i与v_j之间有边 \\ 0& 其他 \end{cases}$     通常，我们需要将拉普拉斯矩阵进行归一化。常用的有两种方式。
    (1) 对称归一化的拉普拉斯矩阵(Symmetric Normalized Laplacian Matrix) $L^{sym}=D^{-\frac{1}{2}}LD^{-\frac{1}{2}}=I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$     (2) 随机游走归一化的拉普拉斯矩阵(Random Walk Normalized Laplacian Matrix) $L^{rw}=D^{-{1}}L=I-D^{-{1}}A$     以下面这个图为例，假设每条边权重为1，得到这个图的邻接矩阵、度矩阵和拉普拉斯矩阵。
图谱论学习—拉普拉斯矩阵背后的含义
    从这个L矩阵中可以观察到拉普拉斯矩阵的以下几条性质。
    ○ L是对称的
    ○ L是半正定矩阵（每个特征值 $\lambda_i{\geq}0$ ）
    ○ L的每一行每一列的和为0
    ○ L的最小特征值为0。给定一个特征向量 $v_0=(1,1,\cdots,1)^T$ ，根据上一条性质，L的每一行之和为0，所以 $Lv_0=0$

三、拉普拉斯矩阵的推导与意义

3.1 梯度、散度与拉普拉斯算子

图拉普拉斯矩阵，如果把它看作线性变换的话，它起的作用与分析中的拉普拉斯算子是一样的。我们将在下面详细讨论，这里需要补充一些基础知识：

梯度定义
梯度 “ $\nabla$ ” 是一个矢量，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该方向处沿着此梯度方向变化最快，变化率最大（梯度的模）。

    假设一个三元函数 $u = f (x, y, z)$ 在空间区域 $G$ 内具有一阶连续偏导数，点 $P(x,y,z){\in}G$ ，则称以下向量表示为点 $P$ 处的梯度：
$\{\frac{{\partial}f}{{\partial}x},\frac{{\partial}f}{{\partial}y},\frac{{\partial}f}{{\partial}z}\}=\frac{{\partial}f}{{\partial}x}\vec{i}+\frac{{\partial}f}{{\partial}y}\vec{j}+\frac{{\partial}f}{{\partial}z}\vec{k}$     该式可记为 $g r a d f (x, y, z)$ 或 ${\nabla}f(x,y,z)$ ，其中：
$\nabla=\frac{{\partial}}{{\partial}x}\vec{i}+\frac{{\partial}}{{\partial}y}\vec{j}+\frac{{\partial}}{{\partial}z}\vec{k}$     称为向量的微分算子或者Nabla算子

散度定义
散度 “ ${\nabla}{\cdot}$ ” （divergence）是一个标量，用于表示空间中各点矢量场发散的强弱程度，物理上，散度的意义是场的有源性。当 $d i v (F) > 0$ ，表示该点有散发通量的正源（发散源）；当 $d i v (F) < 0$ ，表示该点有吸收能量的负源（洞或汇）；当 $d i v (F) = 0$ ，表示该点无源

散度是作用在向量场上的一个算子。用三维空间举例，向量场就是在空间中每一点处都对应一个三维向量的向量函数：
$F(x,y,z)=(v_1(x,y,z),v_2(x,y,z),v_3(x,y,z))^T\\ div(F)=\frac{{\partial}v_1}{{\partial}x}+\frac{{\partial}v_2}{{\partial}y}+\frac{{\partial}v_3}{{\partial}z}$ 它是一个标量函数（场），也就是说，在定义空间中每一点的散度是一个值。矢量 $V$ 的散度在笛卡尔坐标（直角坐标系）下的表达式如下所示：
$\nabla{\cdot}V=\frac{{\partial}V_x}{{\partial}x}+\frac{{\partial}V_y}{{\partial}y}+\frac{{\partial}V_z}{{\partial}z}$

拉普拉斯算子定义
拉普拉斯算子“ $\triangle$ ”（Laplace Operator）是n维欧几里得空间中的一个二阶微分算子，定义为梯度（ ${\nabla}f$ ）的散度（ ${\nabla}\cdot$ ）
${\triangle}f={\nabla}^2f={\nabla}{\cdot}{\nabla}f=div(gradf)$

    在笛卡尔坐标表示下：
${\triangle}f=\frac{{\partial}^2f}{{\partial}x^2}+\frac{{\partial}^2f}{{\partial}y^2}+\frac{{\partial}^2f}{{\partial}z^2}$     n维形式如下：
${\triangle}=\sum_i\frac{\partial^2}{{\partial}x_i^2}$     然后推导离散形式的导数：
$\frac{{\partial}f}{{\partial}x}=f(x+1)-f(x)\\ \frac{{\partial}^2f}{{\partial}x^2}=f''(x)=f'(x)-f'(x-1)=f(x+1)+f(x-1)-2f(x)$     以二维坐标为例，将拉普拉斯算子转化为离散形式：
图谱论学习—拉普拉斯矩阵背后的含义 ${\triangle}f=\frac{{\partial}^2f}{{\partial}x^2}+\frac{{\partial}^2f}{{\partial}y^2}\\=f(x+1,y)+f(x-1,y)-2f(x,y)+f(x,y+1)+f(x,y-1)-2f(x,y)\\=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)$     下面用散度 ${\triangle}f$ 的概念进一步分析：
    1. ${\triangle}f>0$ 时，表示该点为发散源，是散发通量的正源，比如下图中的点 $q_1,q_2,q_4$ 。
    2. ${\triangle}f<0$ 时，表示该点为洞或穴，是吸收通量的负源，比如下图中的点 $q_3$ 。
    3. ${\triangle}f=0$ 时，表示该点无源。
图谱论学习—拉普拉斯矩阵背后的含义     我们将上面的式子用矩阵进行表示如下：
$\begin{bmatrix} 0&1&0\\ 1&-4&1\\ 0&1&0\\ \end{bmatrix}$     实际上，拉普拉斯算子计算了周围点与中心点的梯度差。当 $f (x, y)$ 受到扰动之后，其可能变为相邻的 $f (x - 1, y), f (x + 1, y), f (x, y - 1), f (x, y + 1)$ 之一，拉普拉斯算子得到的是对该点进行微小扰动后可能获得的总增益（或者说是总变化）。
    形象地说，假设上图五个圆点都是人，四条黑线分别牵着两个人，所有人同时用力拉绳子，每个人的力气大小分别为： $f (x, y), f (x - 1, y), f (x + 1, y), f (x, y - 1), f (x, y + 1)$ 。而 ${\triangle}f$ 的值就表示了中间那位可怜的仁兄会被拉跑还是把其他人拉过来以及拉过来和被拉跑的程度。 ${\triangle}f>0$ 时表示他会被拉跑， ${\triangle}f<0$ 表示这家伙大力出奇迹把人全拉过来了， ${\triangle}f=0$ 表示这五个人正在僵持状态，谁都拉不动中间那位同志。

3.2 从拉普拉斯算子到拉普拉斯矩阵

    我们现在将3.1节的结论推广到图：
    假设具有 $N$ 个节点的图 $G$ ，节点 $i$ 的邻域为 $N_i$ ，图上定义一个函数 $f=(f_1,f_2,\cdots,f_n)$ ， $f_i$ 表示函数 $f$ 在节点 $i$ 处的函数值，则对其中一个节点 $i$ 进行微扰，它可能变为图中任意一个与它相邻的节点 $j{\in}N_i$ ， $N_i$ 表示节点 $i$ 的一阶邻域。
图谱论学习—拉普拉斯矩阵背后的含义
    我们已经知道通过拉普拉斯算子可以计算一个点在它所有自由度上微小扰动的增益，则通过图来表示就是任意一个节点 $i$ 变化到节点 $j$ 所带来的增益，设节点 $i$ 与节点 $j$ 之间连边 $e_{ij}$ 的权值为 $w_{ij}$ ，考虑图中边的权值则有：
${\triangle}f_i=\sum_{j{\in}N_i}w_{ij}(f_i-f_j)$     如果假设节点 $i$ 与节点 $j$ 不相邻时 $w_{ij}=0$ ，并将上面的式子进行简化：
${\triangle}f_i=\sum_{j{\in}N}w_{ij}(f_i-f_j)\\=\sum_{j{\in}N}w_{ij}f_i-\sum_{j{\in}N}w_{ij}f_j\\=d_if_i-w_{i:}f\\d_i=\sum_{j{\in}N_i}w_{ij}表示顶点的度\\w_{i:}=(w_{i1},\cdots,w_{iN})表示N维的行向量\\f=\begin{pmatrix} f_1\\ {\vdots}\\ f_N\\ \end{pmatrix}表示N维的列向量$     对于所有的N个节点来说：
${\triangle}f=\begin{pmatrix} {\triangle}f_1\\ {\vdots}\\ {\triangle}f_N\\ \end{pmatrix}=\begin{pmatrix} d_1f_1-w_{1:}f\\ {\vdots}\\ d_Nf_N-w_{N:}f\\ \end{pmatrix}\\=\begin{pmatrix} d_1&{\cdots}&0\\ {\vdots}&{\ddots}&{\vdots}\\ 0&{\cdots}&d_N\\ \end{pmatrix}f-\begin{pmatrix} w_{1:}\\ {\vdots}\\ w_{N:}\\ \end{pmatrix}f\\=diag(d_i)f-Wf\\=(D-W)f\\=Lf$     这里的 $(D - W)$ 实际上就是拉普拉斯矩阵 $L$ 。
    根据前面所述，拉普拉斯矩阵中的第 $i$ 行实际上反应了第 $i$ 个节点在对其他所有节点产生扰动时所产生的增益累积。直观上来讲，图拉普拉斯反映了当我们在节点 $i$ 上施加一个势，这个势以哪个方向能够多顺畅的流向其他节点。谱聚类中的拉普拉斯矩阵可以理解为是对图的一种矩阵表示形式。
    形象点说，我们可以把 $N$ 个节点想象为 $N$ 座山峰， $f_i$ 为山峰 $i$ 的海拔高度，两个节点之间有连边则代表两座山峰之间有路径，拉普拉斯矩阵实际就是嵌入了某一个山峰对在其他山峰上的人的吸引程度，或者说是一种人口流动倾向。
图谱论学习—拉普拉斯矩阵背后的含义
    参考链接：
    1. https://zhuanlan.zhihu.com/p/81502804
    2. https://zhuanlan.zhihu.com/p/238644468
    3. https://zhuanlan.zhihu.com/p/85287578文章来源地址https://www.toymoban.com/news/detail-406970.html