SAR合成孔径雷达距离多普勒（RD）算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了SAR合成孔径雷达距离多普勒（RD）算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.简介

距离多普勒算法（RDA）是在1976至1978年为处理SEASATSAR数据提出来的，该算法于1978年处理出了第一幅机载SAR数字图像。RDA至今仍在广泛使用，它通过距离和方位上频域操作，达到了高效的模块化处理要求，同时又具有了一维操作的简便性。该算法根据距离和方位上的大尺度差异，在两个一维之间使用距离徙动校正（RCMC），对距离和方位都进行了近视的分离处理。

由于RCMC是在距离-方位频域中实现，所以也可以进行高效的模块化处理。因为方位频率等同于多普勒频率，所以该域也称之为“距离多普勒域”。RCMC的“距离多普勒”域实现是RDA算法与其它算法的主要区别点，因而称其为距离多普勒算法。

距离相同而方位不同的点目标能量变换到方位频域后，其位置重合，因此频域中单一目标轨迹校正等效于同一最近斜距处的一组目标轨迹校正。这是算法的关键，使RCMC能在距离多普勒域高效实现。

为了提高处理效率，所有的匹配滤波器卷积都可通过频域相乘实现，匹配滤波及RCMC都与距离可变参数有关。RDA区别于其它频域算法的另一主要特点是较易适应距离向参数的变化。所有运算都针对一维数据进行，从而达到了处理的简便和高效。

1984年，JPL对其进行了二次距离压缩（SRC）改进，以处理中等斜视下的数据。距离压缩中SRC可以补偿距离-方位目标相位历程的耦合，从而有助于消除斜视或大孔径下的相位耦合畸变。

综上所诉，本文将从信号模型出发推导讲解有关RDA算法的实现过程。

SAR合成孔径雷达距离多普勒（RD）算法

2.信号回波模型

假设雷达发射的线性调频连续波，经过解调后点目标的回波的信号模型为：

SAR合成孔径雷达距离多普勒（RD）算法

式中，

SAR合成孔径雷达距离多普勒（RD）算法

由图1表示中，我们很容易根据空间关系得到瞬时斜距的关系：

SAR合成孔径雷达距离多普勒（RD）算法

式中

SAR合成孔径雷达距离多普勒（RD）算法

3.低斜视角RD算法实现过程

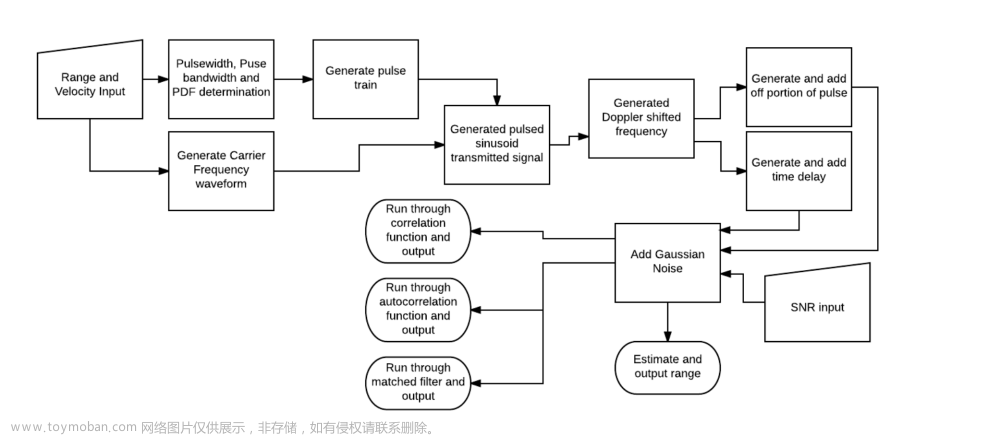
距离多普勒算法（RD）基本思想是将二维处理分解为两个一维处理的级联形式，其特点是只考虑相位展开的一次项，将距离压缩后的数据沿方位向作FFT，变换到距离多普勒域，然后完成距离迁移校正和方位向压缩。算法流程图如图二所示：

SAR合成孔径雷达距离多普勒（RD）算法

有两种实现距离徙动矫正的方式，最传统的RD算法采用的是左边的方法，即在RD域进行插值处理。后来为了提高运算效率，可以通过在Frequency-Azimuth Range域通过乘以一个相位项，反变换回到二维时域来校正距离向发生走动的信号，这个属于改进的RD算法。接下来就从原始的RD算法出发进行讲解。RD算法的主要三个步骤：1.距离向压缩（匹配滤波）2.距离徙动校正 3.方位向脉冲压缩。

3.1 距离向压缩

对回波数据经行距离压缩，首先对式(1)的快时间方向经行FFT，由于式子存在二次项，故直接对其进行傅里叶变换有点困难，故可通过驻相定理（POST）进行求解，有关POST定理的原理可参考[1]。于是根据POST定理得到式（1）的距离向脉冲压缩结果为：

SAR合成孔径雷达距离多普勒（RD）算法

式中A0为常数，压缩脉冲包络Pr为窗函数的傅里叶变换。对于矩形窗，Pr为sin函数。对原始数据利用距离向压缩后，接下来就是将距离压缩后的数据进一步进行处理，将方位向时域转化到频域，并对距离徙动进行补偿。

3.2方位向傅里叶变换

在开始方位向傅里叶变换之前，首先需要对瞬时斜距进行近似处理。在低斜视角的情况下式（2）可以通过泰勒展开近视为：

SAR合成孔径雷达距离多普勒（RD）算法

将式（4）代入（3）式子中可得

SAR合成孔径雷达距离多普勒（RD）算法

观察式（5）可知，从第二个指数项可以明显看到方位相位调制，由于相位是慢时间的二次函数，故在方位向上信号同样具有调频特性，此时调频率为：

SAR合成孔径雷达距离多普勒（RD）算法

式中λ为波长。随后将每一距离上的数据通过方位FFT变换到距离多普勒频域。对于给定目标，式（5）利用POST定理，得到方位向上的时频关系为：

SAR合成孔径雷达距离多普勒（RD）算法

或

SAR合成孔径雷达距离多普勒（RD）算法

将式（8）代入式（5），利用POST得到方位向FFT后的信号为：

SAR合成孔径雷达距离多普勒（RD）算法

联立式（5）和式（8）可以得到距离多普勒域中的RCM，即：

SAR合成孔径雷达距离多普勒（RD）算法

3.3 距离徙动校正

距离徙动校正（RCMC）的实现方法有两种，第一种就是在距离多普勒域中进行距离插值运算，主要的插值算法有最近领插值、牛顿插值、Sinc插值等。本文将基于sinc插值进行讲解。另一种方法则是假设RCM至少在有限区域内不随距离而变，此时可以通过FFT，线性相位相乘以及逆FFT实现RCMC，流程图如图2右。由式子(8)不难得出需要进行校正的距离徙动量为：

SAR合成孔径雷达距离多普勒（RD）算法

通过式(11)不难发现，距离徙动量不仅是R0的函数，同时也是方位频率的函数。对式子（11）经行离散化有：

SAR合成孔径雷达距离多普勒（RD）算法

其中m、n分别为距离向和方位向采样点序号；M、N分别为距离向和方位向采样点数；fs为回波快时间采样率，PRF为脉冲重复频率。我们观察式（3）不难得出一个结论，由于前面说过RCM是目标最近距离R0和方位频率的函数，而在距离压缩后对应不同的最近距离R0和不同的方位频率目标，受斜距影响导致目标在对应的R0和𝑓𝜂中有一个偏移，这个偏移就是式（11），如果这个偏移量比距离分辨率大时，如果不进行补偿将会导致方位向做压缩时候出现散焦现象，只有这个偏移量小于距离分辨率的1/4以上才可以忽视。通过插值的手段，估计出偏移一个距离徙动量的值来实现距离徙动校正。（设未校正前向左偏移一个徙动量，我只需利用现有数据估计向右偏移一个徙动量后的值即为校正后的数据）。另外每一个𝑓𝜂处的距离弯曲量与所占的距离采样单元数Δ𝑚的关系为：

SAR合成孔径雷达距离多普勒（RD）算法

式中P为采样后的距离单元。要校正由斜距产生的弯曲就是从距离多普勒域数据s（m,n）估计得到s（m+Δ𝑚，n）的值，这是一个沿着距离向的插值问题。设校正前的信号为s(m,n),故校正后的信号为S(m,n)：

SAR合成孔径雷达距离多普勒（RD）算法

式(14)即为距离徙动校正公式。通过校正前的信号s(m,n)插值来估计校正后的信号S(m,n)。插值算法主要有最近邻插值、拉格朗日插值、sinc插值等。在这里只介绍sinc插值。

3.3.1 sinc插值

sinc插值法是利用原函数y(x)中其它的点的值进行sinc函数加权得到y(x)在x处的值。

SAR合成孔径雷达距离多普勒（RD）算法

在距离弯曲校正的过程中，考虑到运算量,不可能对回波进行无数点的sinc插值,因此要对sinc插值进行截断处理,取P点的sinc插值，距离弯曲校正的插值公式为:

SAR合成孔径雷达距离多普勒（RD）算法

式中𝑚′为式(13)中Δ𝑚的四舍五入的整数部分，fracn为Δ𝑚的小数部分。由于对sinc的截断会产生Gibbs(吉布斯)效应,所以要对sinc插值核进行加窗,进而减弱Gibbs效应,常用的窗函数有升余弦窗(hamming窗),Kaiser窗。在SAR距离弯曲校正中，兼于精度和运算量的要求,一-般使用8点sinc插值。便于与其他的插值方法比较,文中取4点; 插值进行实验。

4 实验仿真

设置三个点目标，由于篇幅问题参数介绍省略。matlab仿真代码如下：

%作者：poulen 
%时间：2022.12.14
close all; clear; clc;
c = 3e8;   % 光速
fc = 5e9;   %载波频率
B = 200e6;   %带宽
lambda = c/fc;   %波长
Tp = 1.5e-6;    %脉宽
Kr = B/Tp;    %调频率
fs = 1.6*B;     %采样率

H = 200;     %飞机高度
Ls = 200 ;    %合成孔径长度
v = 100 ;     %飞机速度
Lt = Ls/v;    %合成孔径时间

%成像区域[Xc-X0,Xc+X0; Yc-Y0,Yc+Y0]
%以合成孔径中心为原点，距离向为x轴，方位向为y轴
Xc = 10000;
Yc = 0;
Xo = 100 ;
Yo =100 ;

Rc =sqrt(H^2+Xc^2);     %中心距离
Ka = 2*v^2/(Rc*lambda);   %多普勒调频率
Bmax = Lt*Ka;           %多普勒最大带宽
fa = ceil(2.1*Bmax);      %脉冲重复频率

Rmin = sqrt(H^2+(Xc-Xo)^2);   %观测场景距飞机的最近距离
Rmax = sqrt((Xc+Xo)^2+H^2);  %最远距离
rm = Ls + 2*Yo;    %雷达走过的总路程长度
tm= 0:1/fa:rm/v-1/fa;                  %慢时间（合成孔径时间+成像区域时间）
tk= 2*Rmin/c-Tp/2:1/fs:2*Rmax/c-1/fs+Tp/2;       %快时间（距离门内）

target = [Xc,Yc,0;
    Xc-50,Yc+20,0;
    Xc-50,Yc-20,0];        %目标坐标
echo = zeros(length(tm),length(tk),length(target));  %回波
echo_all = zeros(length(tm),length(tk));
y = -v*(rm/v)/2+v*tm;               %飞机y轴坐标
for k=1:size(target,1)  %目标数
    for i=1:length(tm)   %慢时间轴
        radar = [0,y(i),H ];      %飞机坐标
        Rtm = sqrt(sum((target(k,:)-radar).^2));%斜距
        echo(i,:,k)=(abs(target(k,2)-y(i)) < Ls/2)*rectpuls(tk-2*Rtm/c,Tp).*...
                    exp(1j*2*pi*fc*(tk-2*Rtm/c)+1j*pi*Kr*(tk-2*Rtm/c).^2);  %回波模型
    end
    echo_all = echo(:,:,k) + echo_all;
end
r=((tk*c/2).^2-H^2).^(1/2);

%% 距离向匹配滤波
tt=0:1/fs:Tp-1/fs;
for i = 1:size(echo_all,1)
    echo_all(i,:) = echo_all(i,:).*(exp(-1j*2*pi*fc*tk));   %回波去载频
end

hk=exp(-1j*pi*Kr*tt.^2);    %距离向匹配滤波器
MFFT = fft(hk,length(tk));  %匹配滤波频谱
ECHO = zeros(size(echo_all));  %直接距离向压缩之后

%距离校准
% ECHORCMC = zeros(size(echo_all));  %距离校正距离向压缩之后
% f = (-length(tk)/2:length(tk)/2-1)*fs/length(tk); %采样率
% R0 = 2*tk(:)/c;                     %距离门距离
% fm =linspace(-fa/2,fa/2,length(tm)); %慢时间采样率
for i=1:length(tm)
    FasttimeFFT = fft(echo_all(i,:)); 
    ECHO(i,:) = ifft(FasttimeFFT.*MFFT);
%     for n=1:length(tk)
%         deltaR = (lambda*fm(i)/v)^2*R0(n)/8;
%         MFFT(n) = MFFT(n).*exp(1j*4*pi*f(n)*deltaR/c);
%     end
%     ECHORCMC(i,:) = ifft(FasttimeFFT.*MFFT);
end

figure;
[R,Y] = meshgrid(r,y);
mesh(R,Y,abs(ECHO));view(0,90);xlim([9900 10100]);
xlabel('距离向');
title('距离压缩后');

% figure;
% [R,Y] = meshgrid(r,y);
% mesh(R,Y,abs(ECHORCMC));view(0,90);xlim([9900 10100]);
% xlabel('距离向');
% title('距离校准后距离向');
% figure;
% [R,Y] = meshgrid(r,y);
% mesh(R,Y,abs(ECHORCMC-ECHO));view(0,90);xlim([9900 10100]);
% xlabel('距离向');
% title('距离校准后距离向');
% 
ha = exp(-1j*pi*2*(v^2)/(lambda*Rc)*(0:1/fa:Lt-1/fa).^2);  %方位向匹配滤波器
for k=1:length(tk)
    ECHO(:,k) = fftshift(fft(ECHO(:,k)));
end

%% 距离徙动修正
N=6;    %插值核长度为6
ECHO_RCMC=zeros(size(ECHO));
f =linspace(-fa/2,fa/2,length(tm));
for k = 1:length(tm)   
    deltaR = (lambda*f(k)/v)^2*Rc/8;  %注意这个f，到底是哪个f
    DU = 2*deltaR*fs/c;
    du = DU-floor(DU);
    for n = N/2+1:length(tk)  %快时间
        for m = -N/2:N/2-1
            if n+floor(DU)+m>length(tk)
                ECHO_RCMC(k,n) = ECHO_RCMC(k,n)+ECHO(k,length(tk))*sinc(DU-m);
            else
                ECHO_RCMC(k,n) = ECHO_RCMC(k,n)+ECHO(k,n+floor(DU)+m)*sinc(du-m);
            end
        end
    end
end

figure;
[R,Y] = meshgrid(r,y);
mesh(R,Y,abs(ifft(ECHO_RCMC)));view(0,90);xlim([9900 10100]);
title('距离徙动矫正')
xlabel('距离向');

%% 方位向匹配滤波
for k=1:length(tk)
    ECHO(:,k) = abs(ifft(fft(ha,length(tm))'.*fftshift(ECHO_RCMC(:,k)))); %方位向压缩后
end

figure;
mesh(r,y,ECHO);
xlim([9900 10100]);
xlabel('距离向');
ylabel('方位向');
zlabel('幅度'); title('最终压缩结果');

经过距离向压缩后的如下图所示：

SAR合成孔径雷达距离多普勒（RD）算法